大跨径桥梁实时动态挠度信号的分离*

杨 红， 刘夏平， 崔海霞， 彭 军， 孙 卓

(1.广州大学物理与电子工程学院 广州，510006) (2.广州大学土木工程学院 广州，510006)(3.华南师范大学物理与电信工程学院 广州，510006)



大跨径桥梁实时动态挠度信号的分离*

杨 红1， 刘夏平2， 崔海霞3， 彭 军1， 孙 卓2

(1.广州大学物理与电子工程学院 广州，510006) (2.广州大学土木工程学院 广州，510006)(3.华南师范大学物理与电信工程学院 广州，510006)

由于经验模式分解(empirical mode decomposition，简称EMD)将非线性非平稳信号分解成为一系列线性、平稳的本征模函数(intrinsic mode function，简称IMF)信号，针对单通道大跨径桥梁挠度信号分离问题，结合盲源分离和经验模式分解各自优点，提出基于经验模式分解的盲源分离方法。利用奇异值分解(singular value decomposition，简称SVD)估计信号源数目，根据源信号数目将单通道挠度信号和其本征模函数重组为多通道输入信号，应用独立分量分析(independent component analysis，简称ICA)理论中的快速独立分量分析(fast independent component analysis，简称FastICA)算法对输入信号进行分解，实现桥梁挠度信号各分量的分离。仿真研究表明，该方法能较好地解决ICA模型源数估计和单通道挠度信号盲源分离难题。

滤波； 经验模态分解； 独立分量分析； 奇异值分解； 挠度信号分离

引言

挠度是桥梁安全评价中至关重要的参数，荷载与环境的作用、结构材料的变异都可以通过挠度的变化表现出来。按照主成分划分，长期监测系统采集的桥梁挠度数据可看作长期挠度、日温差效应、年温差效应与活荷载效应的叠加[1]。必须分离出各单项因素对桥梁挠度的量值贡献，才能为桥梁的工作性能与安全评估提供可靠的依据。

部分学者对桥梁挠度信号分离进行了相关研究。文献[2]尝试用神经网络方法通过对温度与挠度实测值的样本训练来建立预测模型，该模型根据温度输入值得到相应的挠度，从而将温度产生的挠度值从实时的总挠度中分离出来，然而神经网络方法的有效性取决于原始数据库的完整性和网络结构，而且其训练过程的收敛性也不能保证。文献[3]采用奇异值降解法剔除温度效应的影响，该方法要求各种环境因素的效应与损伤效应不相耦合，同时在健康状态下需得到不同作用效应的所有组合，此条件在实际桥梁中较难满足。文献[4]根据桥梁挠度监测信息具有不同时间尺度的特点，运用小波分析理论剥离活载效应，根据温度效应和温度的相关分析建立温度效应的经验回归方程，剔除结构响应信息中的温度效应。回归统计方法简单易行，但精度较低，且环境因素复杂多变，通过该方法分离某单项因素的作用效应并不可靠。文献[5]同样利用长期监测信号的多尺度特性，结合滤波算法和粒子群优化算法自适应调整滤波器带宽，实现日温差效应分离，滤波算法剔除与其余信号成分的频率区分较明显的目标信号效果较好，但对于日温差挠度、年温差挠度和长期挠度等中心频率接近、带宽重叠的信号成分分离效果较差。

考虑到经验模式分解能够将非线性、非平稳信号自适应地分解成为一系列线性、平稳的本征模函数信号，笔者提出了一种基于经验模式分解的单通道信号盲源分离算法。该算法首先利用EMD分离单通道信号，再将矩阵奇异值分解和Bayesian 信息准则(Bayesian information criterion，简称BIC)结合起来估计信号源数目，将原始信号和IMF信号组合成ICA模型输入信号，欠定ICA问题转化为适定问题，最后进行盲信号分离。这不仅避免了信号稀疏性的限制，也避免了模型参数选择的人为因素。

1 挠度信号分离理论

1.1 EMD算法

经验模态分解可把任意信号分解为一系列内禀模式函数IMF，展现了信号的真实物理信息。EMD是面向数据的，具有自适应特点。

定义x(t)为原信号序列，imfi(t)为经EMD得到的本征模态函数，rn(t)为余量，则原始信号可以表示为所有的imfi(t)及余量之和

(1)

EMD的“筛分”过程见文献[6]。分解过程基于以下假设：a.信号数据至少有一个极大值和一个极小值；b.极值间的时间间隔为特征时间尺度；c.如果信号数据没有极值点而只有拐点，可通过对信号数据进行一次或几次微分来获得极值点，再通过积分获得分解结果。

1.2 ICA基本模型

盲源分离是在源信号与传输通道参数均未知的情况下，根据输入源信号的统计特性，仅由观察信号恢复出源信号独立成分的过程。

假设x=(x1,x2,…，xn)T为n维观测向量，它由原始向量s=(s1,s2,…，sn)T通过混合矩阵A线性组合而成，ICA的基本数学模型为

x=As

(2)

图1 ICA的基本模型Fig.1 Basic model of the ICA

ICA的目的是：在源信号各分量独立的假设下，原始信号s与混合矩阵A都是未知的，寻找一分离矩阵W，使x在通过它后得到的输出信号y(y=Wx)中各分量互相独立，且是s的最佳逼近。ICA分离模型示意图[7]如图1所示。ICA具有几种不同的估计原理和算法，FastICA是一种基于非高斯性极大化原理的算法。采用批处理的方法，在每一步迭代中大量样本数据参与运算，具有收敛更快速、稳健的特点。基于负熵的FastICA算法可以把不定点迭代带来的优良算法特性与负熵带来的统计特性很好地结合起来[8]。

1.3 基于EMD的欠定ICA算法

EMD能够将信号分解成短时单频率组分信号[9]，虽然IMF是信号的一种完备、自适应、基本正交的表达，但EMD具有和二进离散小波分解完全类似的二进滤波器组结构的特性[10-11]，故分解的前几个IMF的带宽过大，使其分解得到的IMF并不完全适用于直接的Hilbert变换而得到精确的瞬时频率谱[12]。

大跨径梁桥挠度观测信号是单通道信号，各种环境因素的效应与损伤效应在低频段相耦合，因此单独使用ICA或EMD算法都不合适。若利用EMD将单通道挠度观测信号进行自适应分解，从一系列IMF信号中选取部分IMF信号和原始观测信号组成ICA模型输入信号，使ICA分离模型输入信号个数和输出信号个数相同，解决了ICA算法中原始观测信号数目小于输出信号数目的欠定问题，因此可将EMD和ICA结合起来应用于大跨径梁桥挠度观测信号盲分离中。

1.4 源数估计

相关矩阵为

(3)

其中：“H”为复数共轭变换。

当噪声是白色信号且噪声对应的本征模函数bimf(t)和源信号对应的本征模函数simf不相关时，式(3)可以简化为

(4)

Rimf(t)的奇异值分解为

(5)

其中：Vs∈RM×l为l个按降序排列的主特征值；Λs=diag{λ1≥λ2≥…≥λl}对应的特征矢量；Vb∈RM×(M-l)为M-l个噪声特征值；Λb=diag{λl+1≥λl+2≥…≥λM}=σ2IM-l对应的特征矢量。

理论上Rimf(t)的M-l个最小特征值等于σ2，因此在假设噪声方差相对小和精确估计协方差矩阵的前提下，通过判断自相关矩阵最小特征值的重复个数可确定其噪声子空间的维数。由于自相关矩阵是由有限长度数据估计出来的，其最小特征值不可能完全相等，且在信号和噪声特征值间设置阈值比较困难，无法判断出噪声子空间的维数。

为解决阈值设置问题，笔者采用Bayesian信息准则估计信号与噪声子空间的维数。BIC信息准则是在Minaka Bayesian选择模型(Minaka Bayesian，简称MIBS)的基础上发展起来的一个真实源数估值有效准则。MIBS的目标是寻找一个能使代价函数最大的序号k(1≤k≤l)，l为非零特征值个数，MIBS计算如下

(6)

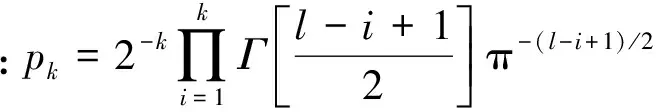
(7)

2 桥梁模拟挠度信号分离

2.1 模拟信号分析计算

图2为一座预应力混凝土连续刚构桥。

图2 背景桥梁示意图(单位：cm)Fig.2 Elevation drawing of the background bridge (unit:cm)

图3 单周期桥梁活荷载挠度曲线Fig.3 The live load deflection curve of the single period′s bridge

假设活荷载效应由车辆荷载引起，采用文献[14]车辆荷载进行结构分析，在车辆以60 km/h行车速度通过桥梁的前提下，以600次/h采样频率采集3天得到活荷载效应结果如图3所示。可以看出，主跨跨中活荷载效应是单周期时域曲线，该信号的时域和频域(为了信号处理方便，且不影响车辆速度的假设，视小时为秒。)波形如图4所示。挠度的其他组分时域和频域(视小时为秒)波形如图5所示(以每小时1次的采样频率采集1年以上的挠度数据)。从图4，5可以看出，活荷载效应频率分布在225Hz附近，日温差效应频率出现在0.41 Hz附近，年温差效应与长期挠度频率出现在0 Hz附近。总挠度的时域和频谱曲线如图6所示。

图4 活荷载效应的时域波形和频谱Fig.4 The time domain curve and spectrogram of the live load effect

图5 各挠度效应的时域和频谱(不包括活荷载效应)Fig.5 The time domain curve and spectrogram of each deflection effect(no including live load effect)

2.2 源信号数的估计

2.3 挠度信号的分离

2.4 结果分析

ICA盲源分离具有两个不确定性：排序的不确定性和幅度的不确定性。评价分离效果可以有多种方法[15-16]，考虑到ICA分离方法的不确定性，为了定量分析信号分离的有效性，采用相关系数作为衡量源信号与相应分离变量相似性的评价指标(因为相关系数不需要考虑幅值问题)。设si为源信号矢量s中的第i个源信号，z为ICA分离算法对s的估计，zi为源信号si对应的分量，则si与其估计值zi之间的相关系数为

图6 总挠度的时域曲线和频谱Fig.6 The time domain curve and spectrogram of the total deflection

图7 分离前后的信号时域曲线比较Fig.7 The signals time domain curve comparison before and after separation

(8)

表1 模拟信号分离前后的信号相关系数

Tab.1 Correlation coefficients of analog signals before and after separation

信号组分si日温差效应年温差效应长期挠度相关系数r0．99900．99350．9755

3 实测挠度数据分离

3.1 实测挠度信号获取

为了说明ICA分离算法的可行性，笔者在各种实测数据的基础上对数据进行适当处理，得到可供分离使用的动态挠度数据，然后进行分离。

活载挠度数据的测取：对广州市琶洲大桥的活荷载挠度进行测取，检测时间为2011年12月16日晚19：00～22：00。图8所示为一段连续20 min的跨中挠度时域曲线，采样频率为18次/s。

图8 活荷载挠度测量时程曲线Fig.8 Measuring schedule curve of the live load deflection

温度效应挠度数据的测取：文献[5]测取了主跨为330 m的某连续刚构桥跨中的由日温差效应与年温差效应叠加形成的竖向位移值，监测时间跨度为1年，采样频率为每隔2 h采样一次，挠度时程曲线如图9所示。

图9 温度效应实测信号Fig.9 The measured signal of the temperature effect

长期挠度信号的测取：文献[17]对2座预应力混凝土连续梁桥(跨径组合为75 m+125 m+75 m和65 m+100 m+65 m)从1997年至2006年的挠度值进行了不定时刻的观测。笔者选取该文献对跨径组合为75 m+125 m+75 m的左幅桥的一段时间测量值(时间跨度为2001年7月至2002年7月)，其挠度变化如图10所示(由于观测时间没有固定，所以图中没有标注时间单位)。

图10 长期挠度实测信号Fig.10 The measured signal of the long-term deflection

3.2 实测数据处理

为说明提出算法对动态挠度信号分离的可行性，对得到的实测信号进行多尺度数据处理。

图11 实测总挠度时-频曲线Fig.11 The time-frequency curve of the measured total deflection

首先，形成一段长度为20 min的动态挠度信号：琶洲大桥的活荷载挠度效应的采集时间为20 min，采样频率为18次/s，因此该数据的长度L=21 600；在20 min的时间内日温差效应、年温差效应、长期挠度的挠度值无明显变化，基本接近恒定值；以18次/s的采样频率对实测的温度效应信号与长期挠度信号在某晚20：00～22：00时刻对应的挠度值进行线性插值;然后，与实测到的活载效应叠加，形成21 600个动态挠度数据；最后，对信号进行多尺度处理，将小时视为秒，将实测活载效应、温度效应与长期挠度的叠加进行频谱变换，如图11所示。依据以上叠加方法，形成时间跨度一年的总挠度。首先，对总挠度进行滤波，剔除活载效应；然后，进行多尺度处理。对数据进行多尺度处理的原因在于：a.在短时间内实测温度效应与长期挠度可以认为变化不大，适当减小采集频率对分离结果没有影响;b.可以避免分离数据量过大而造成的分离算法速度太慢的问题。

3.3 信号分离及结果评价

用以上算法进行相关矩阵的奇异值分解，得到11个特征值量：378.005 8，325.559 9，307.519 5，2.217 7，1.063 3，0.328 3，0.051 8，0.037 6，0.009 1，0.006 7，0.005 1。由Bayesian信息准则可以判断，当k=3时BIC达到最大值，可以确定源数为3。依照分离算法对滤波后的挠度信号进行分离，结果如图12所示。从分离所得信号的时频特征可以判断出它们所属的信号成分。对比图11的原始信号时域曲线容易看出，温度效应得到了很好分离；对比长期挠度分离结果与源信号时域曲线可看出，长期挠度也得到了很好分离。表2为实测挠度源信号与分离结果之间的相关系数。

表2 实测信号分离前后的信号相关系数

Tab.2 Correlation coefficients of the measured signals before and after separation

信号组分si温度效应长期挠度相关系数r0．9870．956

图12 实测挠度效应分离结果Fig.12 Separation results of the measured deflection effect

4 结束语

综合盲源分离和经验模式分解各自的优点，提出了基于EMD的单通道实时动态挠度信号源数估计和盲源分离方法。将欠定盲源分离问题转化为适定问题，深入分析了单通道挠度信号蕴藏的深层状态信息。在综合应用EMD，ICA算法的基础上，实现桥梁挠度信号各分量的分离，从而在挠度监测信号中获取到日、年温差挠度以及长期挠度，实现了盲源分离在桥梁健康评估中的创新应用。模拟信号和实测信号的分离实验结果表明，该算法能很好地分离桥梁挠度信号的分量值。

[1] 刘纲.基于长期静态监测数据的大型桥梁安全状态评估方法研究[D].重庆：重庆大学，2010.

[2] 陈德伟，荆国强，黄峥.用人工神经网络方法估计桥梁在温度作用下的挠度行为[J].结构工程师，2006，22(4)：24-28.

Chen Dewei, Jing Guoqiang, Huang Zheng. Prediction of bridge structural performance under temperature by artificial neural network[J]. Structural Engineers, 2006, 22(4): 24-28. (in Chinese)

[3] Deraemaeker A, Reynders E, Roeck G D, et al. Vibration-based structural health monitoring using output-only measurements under changing environment[J]. Mechanical Systems and Signal Processing, 2008, 22(1):34-56.

[4] 梁宗保.基于监测信息统计分析的桥梁结构安全评价研究[D].重庆：重庆大学，2006.

[5] 刘纲，邵毅敏，黄宗明，等.长期监测中结构温度效应分离的一种新方法[J].工程力学，2010，27(3)：55-61.

Liu Gang, Shao Yimin, Huang Zongming, et al. A new method to separate temperature effect from long-term structural health monitoring data[J]. Engineering Mechanics, 2010, 27(3): 55-61. (in Chinese)

[6] 蒲秀娟，曾孝平，韩亮，等.基于经验模式分解和最小二乘支持向量机的胎儿心电信号提取[J].四川大学学报：工程科学版，2010，42(6)：158-165.

Pu Xiujuan, Zeng Xiaoping, Han Liang, et al. Extraction of fetal electrocardiogram signal using empirical mode decomposition and least squares support vector machines[J]. Journal of Sichuan University:Engineering Science Edition, 2010, 42(6): 158-165. (in Chinese)

[7] 牛雪梅，黄晋英，潘宏侠，等.免疫优化盲源分离算法在故障诊断中的应用[J].振动、测试与诊断，2012，32(2)：306-311.

Niu Xuemei, Huang Jinying, Pan Hongxia, et al. Immune optimation algorithm for blind source separation and its application on fault diagnosis[J]. Journal of Vibration, Measurement & Diagnosis,2012,32(2):306-311. (in Chinese)

[8] Reyhani N, Ylipaavalniemi J, Vigário R, et al. Consistency and asymptotic normality of FastICA and bootstrap FasICA[J]. Signal Processing, 2012,92(8):1767-1778.

[9] 张梅军，陈灏，曹勤，等.基于SVM信号延拓改进的EEMD方法[J].振动、测试与诊断，2013，33(1)：93-97.

Zhang Meijun, Chen Hao,Cao Qin,et al. The improved EEMD method based on SVM signal continuation[J]. Journal of Vibration, Measurement & Diagnosis,2013,33(1):93-97. (in Chinese)

[10]Wu Zhaohua, Huang Norden E. A study of the characteristics of white noise using the empirical mode decomposition method[J]. Proceedings of the Royal Society of London Series A,2004,460: 1597-1611.

[11]Flandrin P, Rilling G, Goncalvés P. Empirical mode decomposition as a filter bank[J]. IEEE Signal Processing Letters,2004,11(2):112-114.

[12]Peng Z K, Tse P W, Chu F L. An improved Hilbert-Huang transform and its application in vibration signal analysis[J]. Journal of Sound and Vibration, 2005, 286(1/2):187-205.

[13]叶红仙.机械系统振动源的盲分离方法研究[D].杭州：浙江大学，2008.

[14]王荣辉，池春，陈庆中，等.广州市高架桥疲劳荷载车辆模型研究[J].华南理工大学学报：自然科学版，2004，32(12)：94-96.

Wang Ronghui, Chi Chun, Chen Qingzhong, et a1. Study on the model of the fatigue-loaded vehicles in guangzhou trestle bridges[J]. Journal of South China University of Technology:Natural Science Edition, 2004, 12(12): 94-96. (in Chinese)

[15]Gao Quanxue, Zhang Lei, Zhang David,et al. Independent components extraction from image matrix[J]. Pattern Recognition Letters,2010,31(3):171-178.

[16]路亮，龙源，钟明寿，等.FastICA算法在低信噪比爆破振动信号信噪分离中的应用研究[J].振动与冲击，2012，31(17)：33-37.

Lu Liang, Long Yuan, Zhong Mingshou,et al. Separating noise from a blasting vibration signal based on fast ICA[J]. Journal of Vibration and Shock,2012,31(17):33-37. (in Chinese)

[17]牛艳伟，石雪飞，阮欣.大跨径混凝土梁桥的长期挠度实测分析[J].工程力学，2008，25(S1)：116-119.

Niu Yanwei, Shi Xuefei, Ruan Xin. Measured sustained deflection analysis of long-span prestressed concrete beam bridges[J]. Engineering Mechanics, 2008, 25(S1): 116-119. (in Chinese)

*国家自然科学基金面上基金资助项目(51078093)；广东省科技计划资助项目(2011B010300026)

2013-02-25；

2013-07-06

10.16450/j.cnki.issn.1004-6801.2015.01.007

TP274; U447； TH113

杨红，男，1967年3月生，博士、副教授。主要研究方向为桥梁智能监测以及智能交通系统的开发。E-mail:yhenryh@sina.com