V型推力杆纵向刚度的预测和优化方法*

柯 俊, 史文库, 滕 腾, 周宇飞, 刘天云, 吴志勇

(1.吉林大学汽车仿真与控制国家重点实验室 长春，130022) (2.中国第一汽车集团公司技术中心 长春,130011)(3.长春成云汽车配件有限公司 长春,130114)



V型推力杆纵向刚度的预测和优化方法*

柯 俊1, 史文库1, 滕 腾2, 周宇飞2, 刘天云3, 吴志勇3

(1.吉林大学汽车仿真与控制国家重点实验室 长春，130022) (2.中国第一汽车集团公司技术中心 长春,130011)(3.长春成云汽车配件有限公司 长春,130114)

为了预测和优化重型商用车V型推力杆的纵向刚度，通过橡胶试样单轴拉压试验建立V型推力杆中橡胶材料的超弹性本构模型，采用Abaqus软件对V型推力杆的工作过程进行有限元动态模拟。利用Abaqus软件的后处理模块预测V型推力杆的纵向刚度，并根据橡胶层的应变云图分析V型推力杆的纵向刚度与球铰结构之间的关系。分析结果表明，增大球铰塑料层的宽度可提高V型推力杆的纵向刚度，原因是这种结构改变了球铰橡胶层的体积及硫化面积，并阻碍橡胶层向两侧端盖的延展。对原结构及优化方案的样件进行台架试验。试验结果表明，提出的预测及优化方法是有效的，可缩短V型推力杆的开发周期，显著提高V型推力杆的纵向刚度。

推力杆; 本构模型; 有限元分析; 刚度优化; 平衡悬架

引言

推力杆是多轴汽车平衡悬架的关键零部件之一。由于重型商用车的服役强度大，其平衡悬架的V型推力杆受力情况非常恶劣，经常出现疲劳失效的现象，严重影响整车的安全性。与此同时，关于V型推力杆的研究才刚起步，仅集中在结构形式、失效分析、静动态特性分析[1]及试验方法的探讨上。因此，急需探索出针对V型推力杆各项性能的优化原理和方法。

纵向刚度是V型推力杆的重要性能指标，该项性能的好坏直接影响V型推力杆的疲劳寿命。这是因为V型推力杆在服役过程中的变形主要来源于其球铰内部的橡胶层，而增加橡胶材料的硬度会导致其疲劳寿命的大幅度下降，因此只能通过改进球铰的内部结构来改善橡胶层的变形状态。V型推力杆的球铰结构不合理，会导致橡胶层在承受载荷时的变形过大，宏观上就体现为纵向刚度不足，这将导致橡胶层的过早失效，使其疲劳寿命下降。因此，如何找出V型推力杆的纵向刚度与其球铰结构之间的关系，从而提出结构优化方案，达到提高V型推力杆纵向刚度的目的，是当前研究面临的难点和关键。

笔者应用有限元法对V型推力杆的工作过程进行有限元动态模拟，通过模拟结果预测V型推力杆的纵向刚度。根据不同球铰结构中橡胶层的应变云图分析V型推力杆的纵向刚度与球铰结构之间的关系，提出了优化方案。通过台架试验验证了优化方案的有效性，并对预测的刚度值进行了修正。

1 V型推力杆有限元模型的建立

1.1 橡胶材料超弹性本构模型的确定

对橡胶材料变形行为的准确模拟是预测V型推力杆纵向刚度的难点和关键。对V型推力杆中橡胶材料的标准试样进行单轴拉压试验，将试验测得的应力应变数据导入Abaqus软件中。Abaqus软件会对试验数据进行去噪处理，自动核查材料的Drucker稳定性，并运用最小二乘法进行数据拟合，计算出超弹性模型的参数[2]。运用常见的超弹性模型对实验测得的应力应变数据进行拟合，各模型的拟合曲线与试验曲线的对比如图1所示。

图1 不同本构模型对橡胶材料的拟合曲线Fig.1 The fitting curves of different constitutive models for rubber material

从图1可看出，与其他超弹性模型相比，1阶Ogden模型能更精确地模拟橡胶材料的应力应变特性。Ogden模型是唯象理论中相对成熟的超弹性本构模型，它用单位体积应变能密度来描述橡胶材料的力学特性，能较好地度量变形，特别适用于大变形材料[3-6]。该模型单位体积的应变能函数[7]为

其中：W为单位体积的应变能；N为材料参数；μi，αi和Di都是和温度相关的材料参数；λi为橡胶的主伸长比；Jel为弹性体积比率。

Ogden模型的初始剪切模量和体积模型分别为

K0=2/D1

在Abaqus软件中，采用一阶Ogden模型对试验测得的应力应变数据进行拟合，建立V型推力杆中橡胶材料的本构模型，将泊松比的值设置为0.49，从而实现对V型推力杆中橡胶材料力学特征的准确模拟[7]。

1.2 有限元模型的建立

采用Catia软件建立V型推力杆的三维几何模型。将建立的三维几何模型导入Hypermesh软件，对各零部件进行网格划分[8]。将模型文件导入Abaqus软件中，将材料属性赋予各单元，并根据实际安装环境及装配关系定义相关零件的接触对、绑定和耦合约束[9-10]。完成网格划分后的V型推力杆如图2所示。

图2 V型推力杆的有限元模型Fig.2 The finite element model of V-type thrust rod

2 V型推力杆纵向刚度预测

2.1 V型推力杆工作过程的动态模拟

V型推力杆的结构复杂，包含橡胶等非线性材料，准确模拟V型推力杆在试验载荷下的工作过程是对V型推力杆的纵向刚度进行预测的前提条件。由于V型推力杆球铰的内部结构具有对称性且有限元模型的规模比较庞大，因此利用Abaqus软件对V型推力杆在试验载荷下的拉伸过程进行动态模拟即可[11]。在V型推力杆的装配过程中，对球铰中的橡胶层施加了较大的压装力，橡胶层的变形状态是压装力和外界载荷叠加作用的结果。

对V型推力杆在试验载荷下的动态模拟应该分成两个阶段。

1) 为了使球铰中的橡胶层产生预变形[12]，在Abaqus软件中通过V型推力杆大端头的端盖对大端头球铰的橡胶层施加105 kN的压装力，通过V型推力杆小端头的端盖对小端头球铰的橡胶层施加70 kN的压装力，并在对应的弹性挡圈上施加了反作用力。各压装力同时从t=0.00 s时开始作用，在t=0.03 s时稳定施加在各端盖上，并保持该状态直到全部模拟过程结束。

2) 为了模拟V型推力杆在试验载荷下的拉伸变形过程[13]，在Abaqus软件中对V型推力杆两个小端头芯轴的端耳施加固定约束，在时间为0.03～0.05 s阶段向大端头芯轴的端耳均匀施加幅值为150 kN纵向拉伸载荷。为了保证V型推力杆的变形状态趋于稳定，设定载荷在时间为0.05～0.06 s阶段保持不变。为了能方便地预测V型推力杆的纵向刚度，利用相关模块在V型推力杆大端头球铰的中心处预先定义了参考点，并要求输出该参考点沿试验载荷方向的位移-时间曲线。由于模型很大，所以设定总模拟时间为0.06 s。

2.2 V型推力杆纵向刚度的预测方法

首先，按照上述建模及模拟方法对特定结构的V型推力杆在试验载荷下的工作过程进行有限元动态模拟；然后，通过Abaqus软件的后处理模块提取大端头球铰中心处预先定义的参考点沿试验载荷方向的位移历程。将150 kN的试验载荷除以参考点在时间为0.05～0.06 s之间的位移平均值，即可得到特定结构下V型推力杆纵向刚度的预测值。

3 V型推力杆纵向刚度优化

V型推力杆大端头的球铰包括芯轴、塑料层、橡胶层及端盖、垫片和外套等外围零件，球铰内部的剖面图如图3所示。考虑工艺及成本因素，芯轴的结构不宜改动。为了降低注塑成型时产生缺陷的概率，塑料层的厚度不宜继续增大。因此，为了分析总结V型推力杆的纵向刚度与球铰结构之间的关系，提出两种改进措施，即增大球铰外围零件(端盖、垫片、外套)的直径和增大球铰塑料层的宽度。

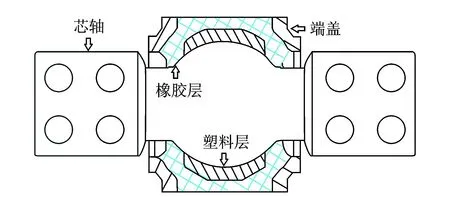
图3 V型推力杆球铰的剖面图Fig.3 The section drawn of the spherical hinge in V-type thrust rod

3.1 球铰外围零件直径的影响

将V型推力杆三维模型中大端头球铰外围零件的直径增大，通过有限元模拟预测V型推力杆的纵向刚度，得到的V型推力杆纵向刚度随大端头球铰外围零件直径的增大而变化的情况如表1所示。

表1 纵向刚度随外围零件直径的增大而变化的情况

Tab.1 The change of longitudinal stiffness with increasing diameter of peripheral parts

直径增大值/mm纵向刚度/(kN·mm-1)变动幅度/%037．037235．714-3．6434．091-8．0

从表1可看出，随着大端头球铰外围零件直径的增大，V型推力杆的纵向刚度有下降的趋势。

3.2 球铰塑料层宽度的影响

将V型推力杆三维模型中大端头球铰塑料层的宽度增大，通过有限元模拟预测V型推力杆的纵向刚度，得到的V型推力杆纵向刚度随大端头球铰塑料层宽度的增大而变化的情况如表2所示。

表2 纵向刚度随塑料层宽度的增大而变化的情况

Tab.2 The change of longitudinal stiffness with increasing width of plastic layer

宽度增大值/mm纵向刚度/(kN·mm-1)变动幅度/%037．0374．639．683+7．16．641．380+11．7

从表2可看出，随着大端头球铰塑料层宽度的增大，V型推力杆的纵向刚度有上升的趋势。

3.3 纵向刚度与球铰结构之间的关系

利用Catia软件计算大端头球铰橡胶层的体积，大端头球铰橡胶层的体积随各参数变化的情况如表3所示。

表3 橡胶层的体积随各参数变化的情况

Tab.3 The volume change of rubber layer with the change of each parameter

方案/mm橡胶层体积/10-4m3体积变动/%刚度变动/%原有结构2．825外围零件直径增大23．034+7．4-3．6外围零件直径增大43．247+14．9-8．0塑料层宽度增大4．62．669-5．5+7．1塑料层宽度增大6．62．621-7．2+11．7

对比表1～3可看出，V型推力杆纵向刚度的变化趋势与球铰橡胶层体积的变化趋势有非常密切的联系：随着外围零件直径的增大，球铰橡胶层的体积和变形空间随之扩大，从而提高了橡胶层的变形潜力，导致V型推力杆的纵向刚度下降；随着塑料层宽度的增大，球铰橡胶层的体积和变形空间随之缩小，从而降低了橡胶层的变形潜力，导致V型推力杆的纵向刚度上升。进一步还发现，增大外围零件直径及增大塑料层宽度这两种措施对调整V型推力杆纵向刚度的效果有强弱之分。从表3看出，在增大外围零件直径的两个方案中，刚度变动幅度仅为对应体积变动幅度的一半；而在增大塑料层宽度的两个方案中，刚度变动幅度为体积变动幅度的1.3倍以上，且随着塑料层宽度增加、幅度的扩大，刚度变动幅度相对体积变动幅度由1.3倍上升至1.6倍。为了探明出现这种现象的原因，利用Abaqus后处理模块提取原有结构、球铰外围零件直径增大4 mm及塑料层宽度增大6.6 mm后大端头球铰内橡胶层的应变云图，分别如图4～6所示。

图4 原有结构橡胶层的应变云图Fig.4 The strain nephograms of rubber layer in the original structure of V-type thrust rod

图5 外围零件直径增大4 mm后橡胶层的应变云图Fig.5 The strain nephogram of rubber layer with which the diameter of peripheral parts increased 4 mm

图6 塑料层宽度增大6.6 mm后橡胶层的应变云图Fig.6 The strain nephogram of rubber layer with which the width of plastic layer increased 6.6 mm

对比图4(a)及图5可看出，球铰外围零件直径增大4 mm后，橡胶层上与端盖内侧硫化处(图中椭圆标示内)拉伸应变最大值由0.862上升至1.978，且拉伸应变较大的部位显著扩大，这说明球铰橡胶层外围环面体积的增加会增大芯轴的位移幅值。因为球铰外围零件的直径增大后，加厚了球铰橡胶层的外围环面。外围环面在承受相同载荷时的变形量增大，导致芯轴的位移幅值增大，从而加剧了对橡胶层上与端盖内侧硫化处(图中椭圆标示内)的拉伸作用。还可以看出，橡胶层外围环面上不承受载荷一侧拉伸应变较大的部位(图中矩形标示内)显著缩小，这说明承受载荷一侧的橡胶层有向两侧端盖方向延展的趋势。这是因为外套内腔的体积是固定的，橡胶承受载荷一侧的橡胶层由于发生了严重的压缩变形，必然试图向两侧端盖方向延展。球铰外围零件的直径增大后，扩大了橡胶层外围环面向两端盖方向延展的通道，使更多的橡胶被挤入外围环面不承受载荷的一侧，从而使外围环面发生拉伸应变的区域缩小。

对比图4(b)及图6可以看出，球铰塑料层宽度增大6.6mm后，橡胶层上与端盖内环面硫化处(图中椭圆标示内)拉伸应变最大值由0.862下降至0.802，且拉伸应变较大的部位显著缩小。这说明球铰塑料层宽度的增加会减小芯轴的位移幅值。因为球铰橡胶层外围环面的体积减小后，外围环面在承受相同载荷时的变形量减小，导致芯轴的位移幅值降低，从而缓解了对橡胶层上与端盖内侧硫化处(图中椭圆标示内)的拉伸作用。还可以看出，橡胶层与塑料层外壁接触环面上的压缩应变最大值由0.011上升至0.066，且压缩应变较大的部位(图中矩形标示内)显著缩小。这一现象说明球铰塑料层的宽度增大后，橡胶层在压缩变形时的延展不够顺畅。这是因为增加的塑料体占据了一部分流动通道，阻碍了橡胶层外围环面向两侧端盖方向的延展，同时增大了橡胶层与塑料层的硫化面积，使橡胶层延展的阻力增大，造成了产生压缩应变的部位相对集中，而且压缩应变的数值显著增大的现象。

3.4 V型推力杆纵向刚度的优化方案

根据对橡胶层体积变化及应力云图分析的结果，要从结构上采取措施提高V型推力杆的纵向刚度，就必须减少球铰橡胶层外围环面的体积，增大橡胶层的硫化面积，并采取措施阻碍橡胶层外围环面在压缩变形时向两侧端盖方向的延展；因此，通过增大球铰塑料层的宽度来提高V型推力杆的纵向刚度是可行的且成本较低。为了防止塑料层与球铰芯轴运动中的极限位置发生干涉，塑料层的宽度最多能增加6.6 mm，因此选择将球铰塑料层的宽度增加6.6 mm，其他结构不变作为优化方案。

4 验证试验

4.1 V型推力杆的台架试验

为了验证优化方案对V型推力杆纵向刚度的优化效果，对V型推力杆原结构的样件及优化方案的样件进行台架试验。将V型推力杆样件装夹在GPA-1000型电液伺服疲劳试验系统的夹具中，计算机通过控制装置向电机发送载荷信号，电机通过液压传动系统驱动作动器向V型推力杆大端头球铰缓慢施加幅值为150 kN、均值为0N的正弦载荷。通过传感器测量试验过程中V型推力杆总成承受的载荷值及大端头球铰中心的位移值，并将信息实时输入计算机。计算机通过专业软件对载荷及位移历程进行实时显示和记录，经过数据处理后即可获得V型推力杆总成的纵向刚度。V型推力杆的装夹状态如图7所示。

图7 V型推力杆的装夹状态Fig.7 The clamping state of V-type thrust rod

4.2 试验结果

试验测得各样件的纵向载荷-位移曲线及经过线性回归分析得到的对应趋势线如图8所示。

图8 各样件的载荷-位移曲线Fig.8 The load-displacement curves of each sample

从图8得到各样件的纵向刚度及其变化情况如表4所示。

表4 各样件的纵向刚度及其变化情况

Tab.4 The longitudinal stiffness of each sample and the change of them

方案纵向刚度/(kN·mm-1)变化幅度/%原有结构58．781优化方案67．674+15．1

从表4可看出，试验测试刚度大于预测刚度，这是由于在有限元建模过程中对模型进行了适当的简化，且橡胶材料的单轴拉压试验数据与实物有一定的误差。经过优化方案优化后，V型推力杆的纵向刚度提高了15.1%，与预测的提高幅值11.7%接近。这说明优化方案的效果显著，且优化效果与预期一致。

5 结 论

1) 利用笔者提出的针对V型推力杆的建模及动态模拟方法可有效预测V型推力杆纵向刚度的变化趋势，提前评价优化方案的优化效果，从而缩短了V型推力杆的开发周期。

2) 从结构上对V型推力杆纵向刚度进行优化的实质是降低球铰橡胶层外围环面的体积，提高橡胶层的硫化面积，并阻碍橡胶层外围环面在压缩变形时向两侧端盖方向的延展趋势。

3) 球铰塑料层加宽6.6 mm后，V型推力杆的纵向刚度提高了15.1%，优化效果显著。

[1] 张红红，陈昆山，张健.空气悬架V型推力杆静动态特性分析[J].拖拉机与农用运输车，2009，36(3):40-42.

Zhang Honghong，Chen Kunshan，Zhang Jian. Static & dynamic analysis of V-type propelling rod in air suspension system[J]. Tractor & Farm Transporter,2009,36(3):40-42. (in Chinese)

[2] 陈志勇.轻型车驾驶室液压悬置性能匹配研究[D].长春：吉林大学，2011.

[3] 李晓芳，杨晓翔.橡胶材料的超弹性本构模型[J].弹性体，2005，15(1)：50-58.

Li Xiaofang, Yang Xiaoxiang. A review of elastic constitutive model for rubber materials[J].China Elastomerics,2005,15(1)：50-58. (in Chinese)

[4] Bergstrom J S，Boycem C. Constitutive modeling of the large strain time-dependent behavior of elastomers[J]. Journal of the Mechanics and Physics of Solids，1998，46(5):931-954.

[5] Yeoh O H. Characterization of elastic properties of carbon black-filled rubber vulcanizates[J]. Rubber Chemistry and Technology，1990，63(5):792-805.

[6] Beda T. Modeling hyperelastic behavior of rubber： a novel invariant-based and a review of constitutive models[J]. Journal of Polymer Science Part B：Polymer Physics，2007，45(1):1713-1732.

[7] Yeoh O H. On the ogden strain energy function[J]. Rubber Chemistry and Technology，1997，70(2):175-182.

[8] 于国飞.HyperWorks在汽车白车身模态分析中的应用[J].振动、测试与诊断，2012,32(1):138-140.

Yu Guofei. Modal analysis of body-in-white of multipurpose vehicle car based on HyperWorks[J]. Journal of Vibration, Measurement & Diagnosis, 2012,32(1):138-140. (in Chinese)

[9] 石亦平，周玉蓉.ABAQUS有限元分析实例详解[M].北京：机械工业出版社，2006：1-3.

[10]庄茁，由小川，廖剑晖，等.基于ABAQUS的有限元分析和应用[M].北京：清华大学出版社，2009：449-465.

[11]Morman Jr K N, Pan T Y. Application of finite-element analysis in the design of automotive elastomeric components [J] .Rubber Chemistry and Technology, 1988,61(3):503-533.

[12]Valeria A, Roel M. FE-modelling of the rubber mould behaviour during press forming of thermoplastic composites[J]. International Journal of Material Forming，2010，3(4):679-682.

[13]王利荣，吕振华.橡胶隔振器有限元建模技术及静态弹性特性分析[J].汽车工程，2002，24(6):480-485.

Wang Lirong, Lü Zhenhua. Finite element modeling of rubber mount and its static elastic characteristic simulation[J]. Automotive Engineering, 2002，24(6):480-485. (in Chinese)

*吉林省重大科技专项基金资助项目(212E362415);吉林大学研究生创新基金资助项目(450060503159)

2013-06-12；

2013-07-19

10.16450/j.cnki.issn.1004-6801.2015.01.008

U463.33; TH136

柯俊,男，1989年2月生，博士研究生。主要研究方向为汽车系统动力学与控制、汽车零部件可靠性。 E-mail：coolkejun@163．com 通信作者简介：史文库，男，1960年10月生，教授、博士生导师。主要研究方向为汽车系统动力学、汽车NVH分析与控制。 E-mail：shiwk@jlu.edu.cn