基于Lempel-Ziv指标的主轴系统退化*

董新峰， 张为民，2， 邓 松

(1.同济大学机械与能源工程学院 上海，201804) (2.同济大学中德学院 上海，201804)



基于Lempel-Ziv指标的主轴系统退化*

董新峰1， 张为民1，2， 邓 松1

(1.同济大学机械与能源工程学院 上海，201804) (2.同济大学中德学院 上海，201804)

为了检测机床主轴系统在使用过程中状态的变化，提出了一种基于复杂度指标的劣化分析方法。以某磨床空转运行时工件主轴系统产生的振动信号为分析对象，采用复杂度指标对磨床在数月使用过程中工件主轴的状态进行判断。分析结果表明，随着使用时间的增加，工件主轴系统产生的振动信号的复杂度增加。为了验证复杂度指标在劣化分析中的有效性，采用复杂度指标对美国凯斯西储大学公布的劣化轴承数据进行分析，结果表明，该方法在劣化分析中是可行的。

复杂度； 退化； 主轴系统； 轴承； 故障

引言

旋转设备的状态监测在工业生产中具有重要意义，国内外对其进行了大量研究，如轴承状态监测[1-4]、离合器状态监测[5]、液压系统状态监测[6]、柴油机状态监测[7]、电机组状态监测[8]和齿轮箱状态监测[9]等。主轴系统是机床中最重要的组件之一，它主要包括主轴、轴承和主轴箱体，其主要作用是将运动和动力传给工件或刀具并带动刀具或工件运动，进而完成工件的表面成形运动。一般情况下，工件或刀具安装在主轴的前端，直接参与切削加工，因此会对工件的加工质量产生直接影响。统计表明，主轴系统的性能对机床的加工精度影响最大；因此，对主轴系统状态进行监测并分析其性能变化，对机床机械加工精度的控制具有重要意义。

一般情况下，机床经过磨合期后，主轴系统的各项指标能够满足生产需求。当机床在使用、维修和闲置过程中，由于摩擦磨损、疲劳、腐蚀和冲击振动等原因，机床主轴系统的性能会发生变化，导致机床机械加工精度降低，这种性能变化称为机床主轴系统的劣化。通常情况下，主轴系统在一个寿命周期内会经历以下4种劣化状态：正常状态、微小劣化状态、劣化恶化状态及故障状态。如果能够在主轴系统的劣化过程中对其进行检测、判断主轴系统的劣化趋势，就可以有效组织维修，避免主轴系统出现严重故障，最大程度地减小其对机床机械加工精度的影响。因此，主轴系统的劣化分析在生产中具有重要的实际价值。目前，退化分析主要有隐马尔科夫模型方法[10]、高斯混合模型方法[11]、逻辑回归方法[12]、支持向量机方法[13]、人工神经网络方法[14]、关联维数[15]和近似熵指标[16]等。隐马尔科夫模型方法、逻辑回归方法、支持向量机方法和人工神经网络方法属于监督性学习方法，需要训练样本对模型进行训练。当设备训练样本不能获得时，劣化分析将不能进行。高斯混模型方法属于非监督学习方法，不需要故障样本对模型进行训练，通过正常的数据样本就能对设备的劣化情况进行分析。此方法不需要训练数据，在工程应用中更加符合实际；但高斯混合模型方法存在一个缺陷，即特征值的选择较为严格，而且会对模型分布产生大的影响。

在实际中，机床主轴系统的寿命周期较长，故障数据样本很难获得，基于训练样本的劣化分析在主轴系统的劣化分析中是不可行的。关联维数、复杂度指标和近似熵指标是非线性时间序列分析中常用的指标。关联维数和近似熵指标主要通过对测量数据进行状态空间重构，分析重构区间的特点，进而对信号的复杂性进行判断。在数据运算过程中，需要确定重构空间的维数m值和阈值r，当m和r不相同时得到的数据结果也不同，且数据处理时间较长。

采用复杂度指标分析离散数据的复杂性时，只需要对数据进行粗粒化、比较和计数操作，不需要对离散数据进行相空间重构，数据处理时间短。在复杂度算法中要对数据进行粗粒化处理，因此复杂度指标具有强的抗干扰能力。笔者选择复杂度指标对磨床主轴系统的劣化状态进行分析。

1 理论方法

1.1 复杂度指标的定义

复杂度指标能够通过少量的数据对非线性动力学系统的特性进行衡量。复杂性指标在心电、脑电分析中具有广泛应用。文献[17-18]采用复杂度分析脑电信号，并对病人的麻醉状态做出判断。文献[19]通过分析胎儿心率的复杂度指标分析胎儿宫内生长受限情况。文献[20]采用复杂度指标分析患有老年痴呆症的脑磁图(脑磁图)中的信号。文献[21]采用复杂度指标分析了癫痫患者的脑电图。文献[22]采用复杂度指标对心律失常进行了检测。

目前，已有多种复杂度指标，如C0复杂度、Lempel-Ziv复杂度和语法复杂度等。文献[23]提出有限时间序列复杂度的定义，主要用来描述时间序列的复杂程度，步骤如下。

1) 有限长时间序列的粗粒化：设有限长时间序列X=(x1,x2,…,xn)，对X求平均值，将大于平均值的数xi(i=1,2,…,n)记为“1”，小于或者等于平均值的数xi记为“0”，此过程称为粗粒化操作。经过粗粒化操作，时间序列X变为一个由(“0”，“1”)符号组成的时间序列记为S=(s1,s2,…,sn)。

2) 在S序列中选择一个子串S=(s1,s2,…,sm)，在子串S后添加一个符号Q=sm+1或者一个符号串Q=(sm+1,sm+2,…,sm+k)，可以得到一个包括 “0”，“1”的序列SQ=(s1,s2,…,sm,sm+1)或者SQ=(s1,s2,…,sm,sm+1,sm+2,…,sm+k)。令SQv=(s1,s2,…,sm)或SQv=(s1,s2,…,sm，…，sm+k-1)，判断是否存在某个变量i，1≤i≤m，使(sm+1,sm+2,…,sm+k)=(si,…,si+k-1)。如果存在某个i，则称Q为“复制”，然后把Q延长，重复上面步骤，直到Q不属于SQv的一个子串。当Q不属于SQv中的一个子串时，则称Q为“插入”。若“插入”时用小数点“.”标记在Q后，然后把小数点“.”前面的所有符号看成S重复以上步骤，直到序列结束。

3) 通过步骤2能够得到一个由小数点“.”分隔的时间序列，把时间序列的段数记为“复杂度”c(n)。

4) 依照Lempel和Ziv的研究，可以知道复杂度指标按概率趋向一个稳定的数值，即

b(n)是有限长时间序列S的渐进稳定值，用其对c(n)进行归一化，可以得到复杂度指标为

1.2 复杂度与信号的关系

为了说明信号特征与复杂度之间的关系，构造振动信号

S(n)=X(n)+e(n)

其中：X(n)为基本信号；e(n)为噪声信号。

信噪比(signal noise ratio, 简称SNR)定义为

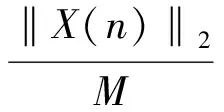
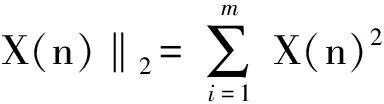
构建不同信噪比信号，其图形如图1所示。表1为信号在不同信噪比下的复杂度值。图2为不同信噪比信号相应的频谱图。从表1可以看出，当信噪比值降低时，复杂度值增加，这相当于退化的数据质量或增长的机器缺陷。然而，这种趋势在图2中没有观测到，它是通过传统的频谱分析技术获得的。这个例子说明，传统的频谱技术在有效表征机器微小健康状态变化方面是有局限性的，同时表明在微小健康状态检测方面，复杂度是一种有效的方法。

表1 不同信噪比信号的复杂度值

2 基于复杂度的主轴系统退化检测

图1 不同信噪比信号波形图Fig.1 Waveform diagram of different SNR signals

为了分析机床在使用过程中主轴系统的退化情况，选择某机床厂M1432B型万能外圆磨床工件主轴和砂轮主轴为检测对象。M1432B型万能外圆磨床于2007年5月出厂，同月开始投入使用。从2007年5月开始，磨床基本每天都在运行且该磨床没有发生过故障。笔者从2010年4月开始对该磨床工件主轴进行检测，到2010年10月停止检测，这里主要以6个月检测的振动信号为分析对象，对M1432B型万能外圆磨床工件主轴和砂轮主轴进行退化分析。从2010年4月开始，每个月对此外圆磨床工件主轴和砂轮主轴进行一次测量，采集振动信号时采样频率设为10 kHz，每次采集时间为10 s，振动传感器的安装位置如图3所示，实验设备配置如表2所示。在每一次测量中磨床按照下列的方式运行：磨床砂轮主轴静止，工件主轴分别以45，67.5，90，112.5和135 r/min速度空转，采用三向加速度传感器测量工件主轴x2,y,z三个方向的振动信号。在磨削加工中，工件主轴水平方向是工件的误差敏感方向，因此主要对x2方向数据进行分析。为了说明退化分析步骤，以工件主轴x2方向的数据为分析对象对数据处理步骤进行说明。

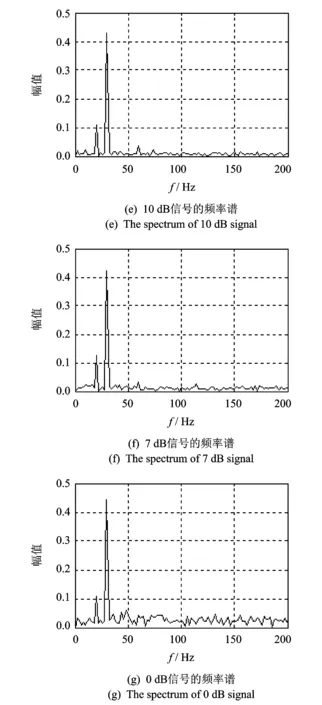
图2 不同信噪比信号的频谱图Fig.2 Spectrum of different SNR signals

图3 M1432B型万能外圆磨床以及传感器安装位置Fig.3 M1432B grinding machine and Sensor mounting position

表2 实验设备配置

1) 振动信号的频域滤波：根据M1432B型万能外圆磨床工件主轴系统的内部结构和主轴转速，对4～10月工件主轴不同转速时x2方向的振动信号进行频域滤波，保留振动信号0～500 Hz频段内的振动信号，运算结果如图4～9所示。

图4 4月份振动信号0～500 Hz低通滤波Fig.4 Low pass filter (0～500 Hz) of signal in April

图5 5月份振动信号0～500 Hz低通滤波Fig.5 Low pass filter (0～500 Hz) of signal in May

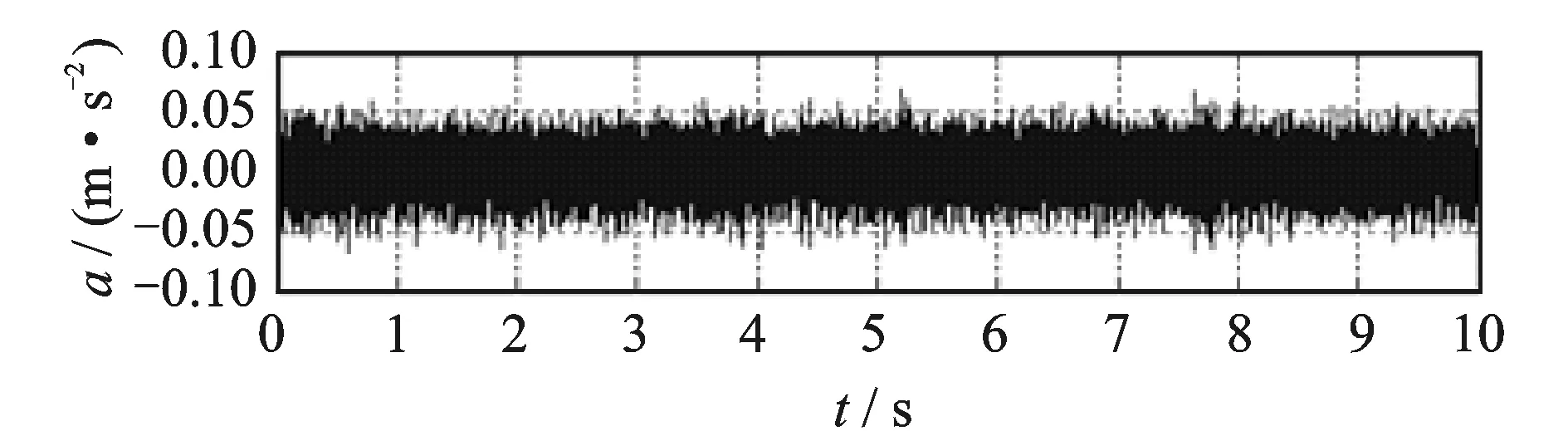
图6 6月份振动信号0～500 Hz低通滤波Fig.6 Low pass filter (0～500 Hz) of signal in June

图7 8月份振动信号0～500 Hz低通滤波Fig.7 Low pass filter (0～500 Hz) of signal in August

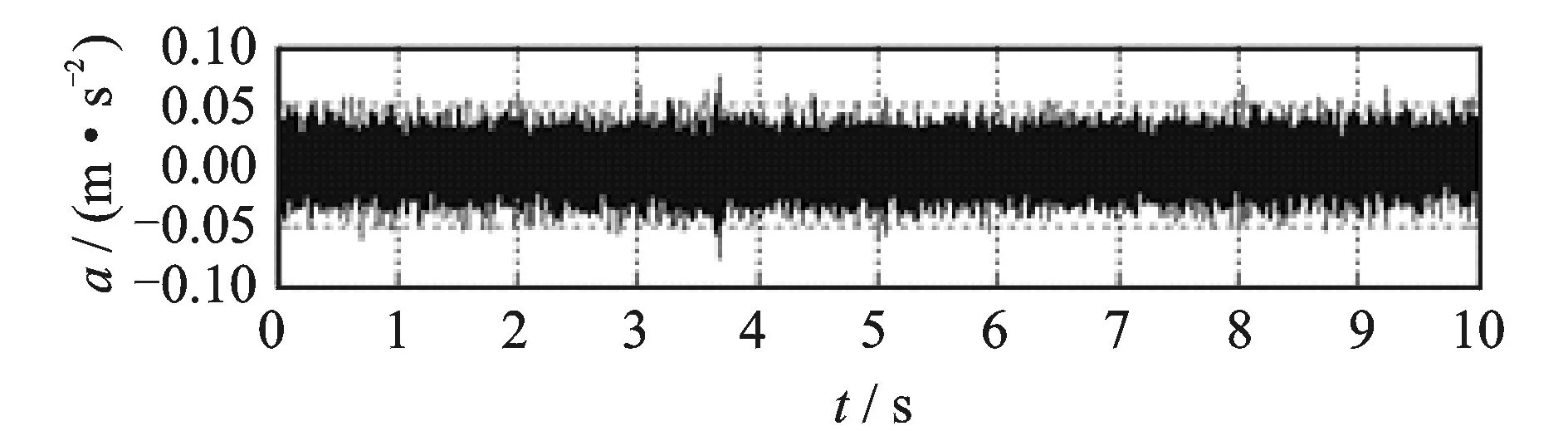
图8 9月份振动信号0～500 Hz低通滤波Fig.8 Low pass filter (0～500 Hz) of signal in September

图9 10月份振动信号0～500 Hz低通滤波Fig.9 Low pass filter (0～500 Hz) of signal in October

2) M1432B型磨床工件主轴每旋转一圈，工件主轴系统内部结构所激发的振动信号能够反映主轴系统内部的状态，取工件主轴每一转对应的振动信号作为研究对象，根据复杂度算法计算每一月不同转次振动信号的复杂度(每一个月共研究22转振动信号的复杂度值)。

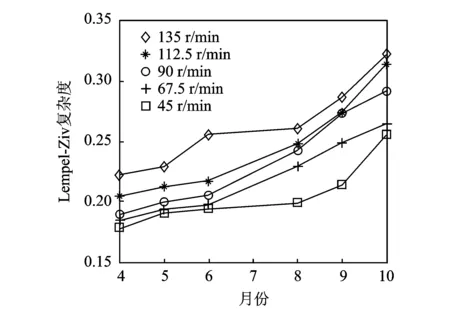
图10 每一月份复杂度值的平均值Fig.10 Average complexity of each month

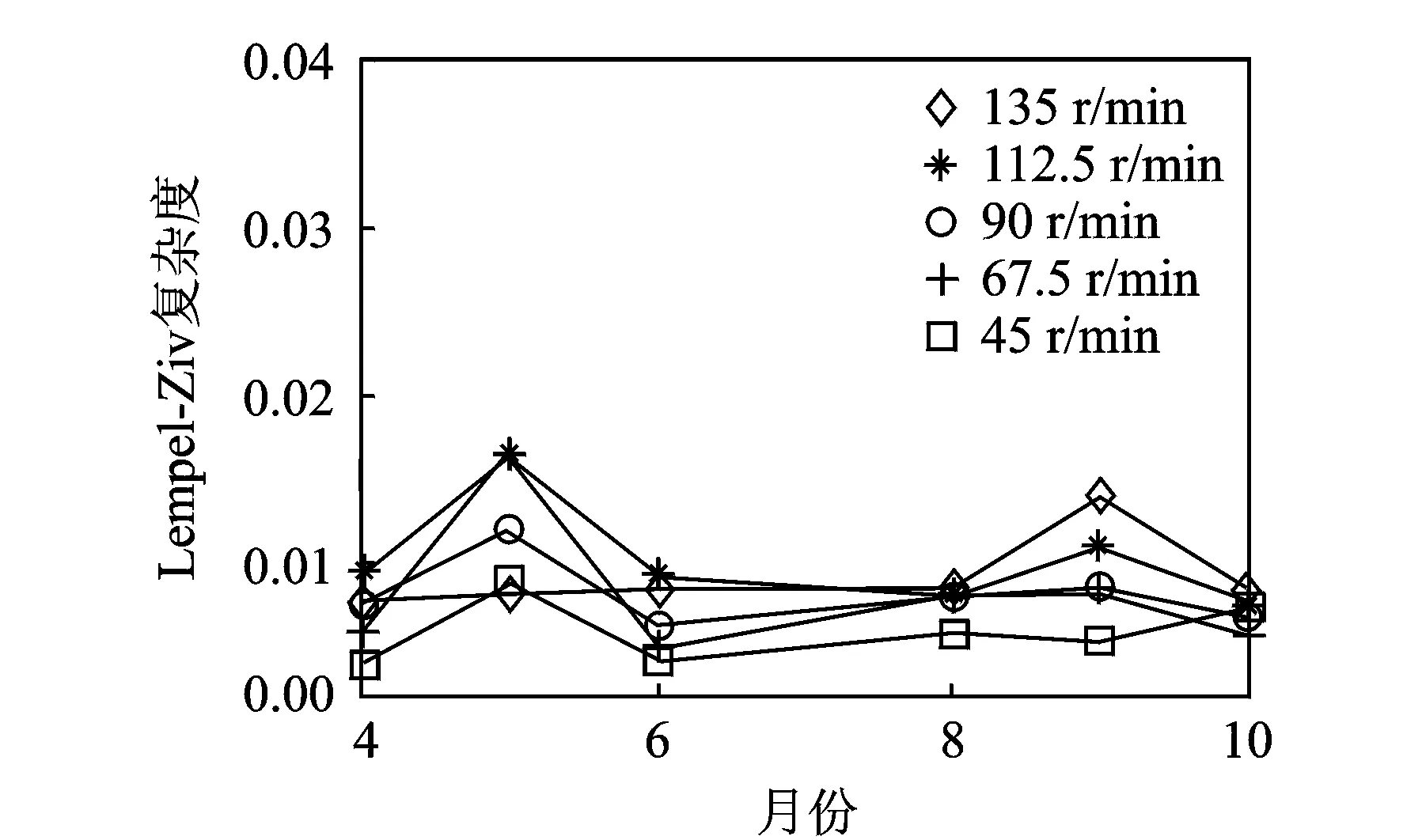
图11 每一月份复杂度值的标准差Fig.11 Standard deviation of each month

3) 求每一月份不同转次复杂度值的平均值和标准差值，以该平均值作为每个月的特征值，通过特征值的变化判断工件主轴x2方向的退化情况，如图10，11所示。从图10可以看出，转速越高对应的复杂度值越大。这是因为当转速升高时，工件主轴系统产生的振动信号的频率成分增加，导致复杂度值的增加，说明复杂度值与转速之间具有明显的线性关系。从图11可以看出，每一月份复杂度值的标准差比较小，这说明复杂度指标具有较强的抗干扰能力。

3 实验验证

如图12所示，该实验平台由电动机(1.491 kW)、测试轴承(选用驱动端轴承为研究对象)、风机(负载)和加速度计等组成，采样频率为12 kHz。实验平台按照如下方式运行获得实验数据：电动机以1 797 r/min的速度旋转，空载运行(不拖动风机)，驱动端轴承内圈分别存在直径为0.177 8，0.355 6，0.533 4，0.711 2 mm，深度为0.279 4 mm的人为缺陷(缺陷采用电火花方式加工)，用加速度计测量驱动端的振动信号。

图12 美国凯斯西储大学测试平台Fig.12 Test platform of CWRU

驱动端轴承的型号为6205-2RS JEM SKF，其具体参数如表3所示。轴承各个组成部分的故障频率如表4所示。

表3 轴承结构参数

Tab.3 Bearing structure parameters mm

内圈尺寸外圈尺寸壁厚滚动体直径节径25．001251．998815．00127．940039．0398

表4 轴承故障频率

Tab.4 Bearing fault frequencies Hz

内圈外圈保持架滚动体5．41523．58480．398284．7135

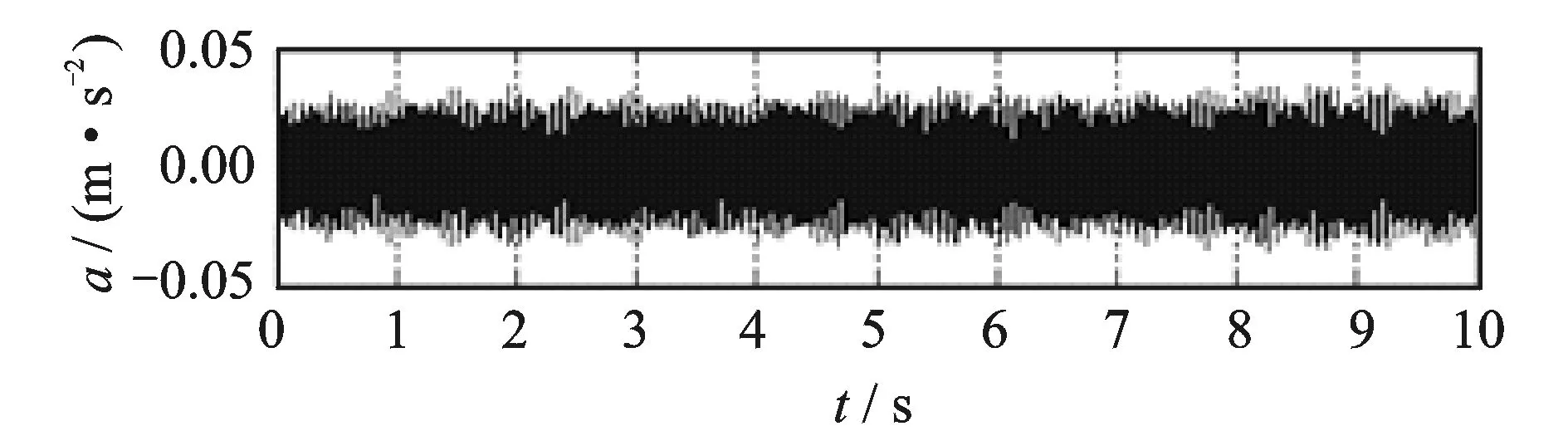
图13 内圈0.177 8 mm缺陷滤波后的振动信号Fig.13 Filtered vibration signal of 0.177 8 mm defect in bearing inner ring

图14 内圈0.355 6 mm缺陷滤波后的振动信号Fig.14 Filtered vibration signal of 0.355 6 mm defect in bearing inner ring

图15 内圈0.533 4 mm缺陷滤波后的振动信号Fig.15 Filtered vibration signal of 0.533 4 mm defect in bearing inner ring

图16 内圈0.711 2 mm缺陷滤波后的振动信号Fig.16 Filtered vibration signal of 0.711 2 mm defect in bearing inner ring

根据驱动端滚动轴承的结构参数、对应的故障频率以及电动机的转速1 797 r/min可以得到轴承在内圈存在一个缺陷时冲击振动频率约为160 Hz，在160 Hz处延拓一定的频段，选择100～200 Hz频段为研究对象，振动信号滤波后的波形如图13～16所示。同理，根据M1432B型磨床工件主轴x2方向数据处理步骤，得到轴承在不同退化程度时对应的平均复杂度值，如表5所示。 可以看到，随着轴承退化程度的增加，复杂度值的趋势项呈上升趋势，说明复杂度指标在退化分析中是可行的。同理，复杂度指标在机床主轴系统的退化分析中也是有效的。

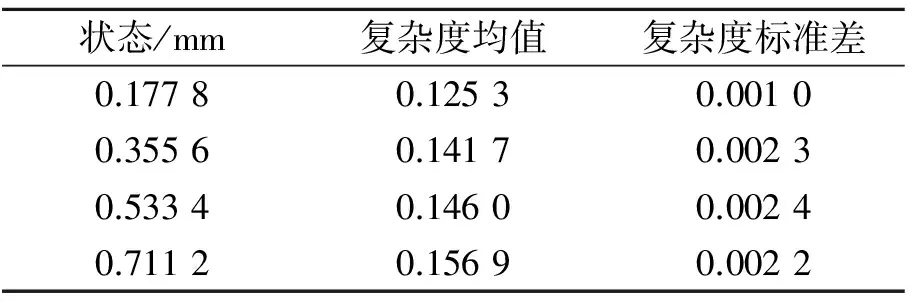
表5 振动信号的复杂度均值

4 结 论

1) 采用复杂度指标分析了磨床在6个月使用过程中主轴系统振动信号复杂度的变化情况。分析结果表明，随着使用时间的增加，主轴系统振动信号的复杂度值呈上升趋势，同时发现主轴系统转速的变化不会对复杂度变化趋势产生影响。可见，对一种转速旋转时测量的振动信号进行分析就能反映主轴系统复杂度的变化情况。

2) 采用美国凯斯西储大学公布的轴承数据对复杂度指标在退化分析中的有效性进行了验证。分析结果表明，随着轴承退化程度的增加，复杂度指标呈上升趋势，可见复杂度在退化分析中是有效的，同时也说明磨床主轴系统发生了轻微退化，而在实际中发现，6个月观察中工件的加工精度确实发生了轻微变化。综上所述，复杂度指标在主轴系统的退化分析中是可行的。

[1] 操礼林,李爱群,邓扬，等.声发射和小波包分析在损伤状态监测中的应用[J].振动、测试与诊断,2012,32(4):591-595.

Cao Lilin, Li Aiqun, Deng Yang, et al. Combined application of acoustic emission and wavelet packet analysis on damage condition monitoring of structures[J]. Journal of Vibration, Measurement & Diagnosis, 2012,32(4):591-595. (in Chinese)

[2] 蔡剑华,胡惟文,王先春.基于高阶统计量的滚动轴承故障诊断方法[J].振动、测试及诊断,2013,33(2):298-301.

Cai Jianhua, Hu Weiwen, Wang Xianchun. Higher-order statistics roller bearing fault diagnosis Gauss noise[J]. Journal of Vibration, Measurement & Diagnosis, 2013,33(2):298-301. (in Chinese)

[3] 王灿,王嘉乐,会强.Hilbert Huang变换在机车滚动轴承故障诊断中的应用[J].振动、测试及诊断,2013,33(1):184-187.

Wang Can, Wang Jiale, Hui Qiang. Locomotive rolling bearing fault diagnosis Lab VIEW Hilbert-Huang transform (HHT)[J]. Journal of Vibration, Measurement & Diagnosis, 2013,33(1):184-187. (in Chinese)

[4] 苑宇,赵兴,赵玉龙.基于时频维数的轴承故障诊断方法[J].振动、测试及诊断,2013,33(1):154-156.

Yuan Yu, Zhao Xing, Zhao Yulong. A method of bearing fault diagnosis based on factral dimensions of time-frequency domain[J]. Journal of Vibration, Measurement & Diagnosis, 2013,33(1):154-156. (in Chinese)

[5] 张志刚,石晓辉,周晓军.分形特征在湿式离合器磨合状态预测中的应用[J].振动、测试与诊断,2011,31(6):783-787.

Zhang Zhigang, Shi Xiaohui, Zhou Xiaojun. Applicationof fractal featuresin predictionof the wet clutch wear-in state[J]. Journal of Vibration, Measurement & Diagnosis, 2011,31(6):783-787. (in Chinese)

[6] 鲁帆, 陈前.液压系统组合协整模型状态监测[J].振动、测试与诊断,2011,31(4):409-414.

Lu Fan, Chen Qian. Condition monitoring of hydraulic flap servo systems using synthes is cointegration model[J]. Journal of Vibration, Measurement & Diagnosis, 2011,31(4):409-414. (in Chinese)

[7] 李宏坤,马孝江.基于KPCA SVM的柴油机状态识别方法的研究[J].振动、测试与诊断,2009,29(1):42-45.

Li Hongkun, Ma Xiaojiang. Pattern recognition of diesel engine by using kernel principle component analysis and support vector machine[J]. Journal of Vibration, Measurement & Diagnosis, 2009,29(1):42-45. (in Chinese)

[8] 盛迎新,周继威.风电机组在线振动监测系统及现场应用[J].振动、测试及诊断,2010,30(6):703-705.

Sheng Yingxin, Zhou Jiwei. Online wind turbine vibration monitoring system and its application[J]. Journal of Vibration, Measurement & Diagnosis, 2010,30(6):703-705. (in Chinese)

[9] 程珩,黄超勇,张永刚.基于粒子群优化决策树的齿轮箱故障诊断[J].振动、测试及诊断,2013,33(1):153-156.

Cheng Hang, Huang Chaoyong, Zhang Yonggang. Constructed of SVM decision tree based on particle swarm optimization algorithm for gear box fault diagnosis[J]. Journal of Vibration, Measurement & Diagnosis, 2013,33(1):153-156. (in Chinese)

[10]朱义,陈进.基于CHMM的设备性能退化评估方法的研究[J].振动与冲击,2008,27(8):110-112.

Zhu Yi, Chen Jin. Research on CHMM based equipment performance degradation assessment[J]. Journal of Vibration and Shock, 2008,27(8):110-112. (in Chinese)

[11]Liao Linxia. A novel method for machine performance degradation assessment based on fixed cycle features test[J]. Journal of Sound and Vibration, 2009,323:894-908.

[12]Yan Jihong, Lee J. Degradation assessment and fault modes classification using logistic regression[J]. Journal of Manufacturing Science and Engineering, 2005,127(4)：912-914.

[13]雷金波.基于逻辑回归和支持向量机的设备状态退化评估与趋势预测研究[D].上海：上海交通大学,2008.

[14]Lee J. Measurement of the machine performance degradation using a neural network model[J]. International Journal of Computers in Industry, 1996,30(3):193-209.

[15]刘天雄，华宏星.基于分形几何状态检测方法的应用研究[J].机械工程学报,2001,37(5):100-103.

Liu Tianxiong, Hua Hongxing. Research on condition monitoring of machinery using fractal geometry[J]. Chinese Journal of Mechanical, 2001,37(5):100-103. (in Chinese)

[16]Yan Ruqiang, Robert G X. Machine health diagnosis based on approximate entropy[J]. Instrumentation and Measurement, 2004,3:2054-2059.

[17]Zhang X S, Roy R J. EEG complexity as a measure of depth of anesthesia for patients[J]. Biomedical Engineering, 2001,48:1424-1433.

[18]Zhang X S, Roy R J. Predicting movement during anesthesia by complexity analysis of the EEG[J]. Medical and Biological Engineering and Computing, 1999,37(3):327-334.

[19]Ferrario M, Signorini M G, Magenes G. Complexity analysis of the fetal heart rate variability: early identification of severe intrauterine growth-restricted fetuses[J]. Medical and Biological Engineering and Computing, 2009,47(9):911-919.

[20]Carlos G, Roberto H. Complexity analysis of the magnetoencephalogram background activity in Alzheimer′s disease patients[J]. Medical Engineering and Physics, 2006,28(9):851-859.

[21]Liu C C, Pardalos P M, Chaovalitwongse W A, et al. Quantitative complexity analysis in multi-channel intracranial EEG recordings form epilepsy brains[J]. Journal of Combinatorial Optimization, 2008,15(3):276-286.

[22]Xu Lisheng, Zhang David, Wang Kuanquan, et al. Arrhythmic pulses detection using Lempel-Ziv complexity analysis[J]. EURASIP Journal on Applied Signal Processing, 2006:1-12.

[23]Lempel A, Ziv J. On the complexity of finite sequences[J]. Information Theory, 1976,22(1):75-81.

*国家科技重大专项基金资助项目(2011ZX04016-021，2012ZX04005031)；国家科技支撑计划资助项目(2012BAF01B02)

2013-07-01；

2013-12-06

10.16450/j.cnki.issn.1004-6801.2015.01.003

TH17； TP206

董新峰，男，1985年10月生，博士研究生。主要研究方向为机械加工切削稳定性、机械设备健康监测及故障诊断。曾发表《基于EMD复杂度与鉴别信息的磨削颤振预测》(《振动、测试与诊断》2012年第4期)等论文。 E-mail：laile_sd@163.com 通信作者简介：张为民，男，1965年1月生，博士、教授、博士生导师。主要研究方向为机械制造及自动化。 E-mail：iamt@tongji.edu.cn