摆幅对仿金枪鱼尾鳍推进性能的影响

艾贤祖， 宋显成， 赵国平

(北京精密机电控制设备研究所, 北京 100076)

相较于传统螺旋桨推进, 鱼类的推进方式实现了桨舵一体, 具有高机动、高效率和低扰动等优点。而在鱼类众多的推进方式中, 以鲹科鱼类为代表的身体-尾鳍推进模式(body and/or caudal fin, BCF)机动性能较好、巡游速度快, 是优良的仿生样本。该模式主要依靠鱼类身体的波动及尾部的摆动产生推进力, 其中鲹科鱼类通常通过短时爆发、 长时滑行来减少效率损失[1], 在这个过程中尾部的摆动将直接影响推进性能的好坏。尤其是作为鱼尾主要部分的尾鳍, 其运动参数对推进性能有着重要影响。研究表明[2], 相较于升沉幅值,摇摆幅度对尾鳍推进性能的影响要大得多。因此研究摆幅对尾鳍推进性能的影响有着更重要意义。

针对尾鳍运动参数对其推进性能影响,许多学者开展了研究。俞经虎等[3]通过一种三节仿生机器鱼模型,分别计算水动力和惯性力引起的尾鳍驱动力矩的值。刘军考等[4]通过实验研究表明, 在一定摆动频率范围内, 推进速度与摆动频率在一定范围内近似成正比关系, 而当摆动频率一定时, 推进速度与摆幅在一定范围内近似成正比关系。张曦等[5]通过数值计算及实验得出, 随着斯特劳哈尔数增大,仿金枪鱼尾鳍的平均推力系数增大,推进效率降低。刘葳兴等[6]以能量的视角提出一种对刚性和柔性拍动翼都适用的推进效率数值计算方法, 并系统地研究了各参数对三维柔性翼推进性能的影响。胡健等[7]采用计算流体力学方法分析了摆动水翼的水动力特性, 详细分析了翼型的水动力性能随斯特劳哈尔数(Strouhal number)Sr的变化的影响。

对比其他形状尾鳍, 金枪鱼的月牙形尾鳍具有极其出色的推进性能[8],有着可预见的广阔应用前景。同时,鉴于摆幅对其推进性能影响的重要性,以金枪鱼尾鳍形状特征为分析对象, 基于浸入边界法(immersed boundary method,IBM)开展摆幅对其推进性能影响研究。首先,对金枪鱼尾鳍外形特征以及运动特征进行数学描述,并建立模型。然后,以苏玉民等[2]进行的摆动尾鳍试验为算例,对比验证了浸入边界数值方法的可行性。最后,在给定斯特劳哈尔数条件下, 对比分析仿金枪鱼尾鳍在不同摇摆幅度下推进性能的变化,并提炼相关规律，为水下仿金枪鱼尾鳍推进机构的设计和控制提供参考。

1 数值方法验证

1.1 浸入边界法简介

浸入边界法(IBM) 是采用欧拉变量去描述流体的动态、利用拉格朗日变量描述结构的运动边界、用光滑Delta近似函数通过分布节点力和插值速度来表示流场和结构物的交互作用的方法[9]。它整个流场计算都使用笛卡尔网格, 无需处理从物理平面到计算平面的坐标和网格转换问题, 因而可以大大提高计算效率，而且节省了网格生成所需的时间[10]。

浸入实体 (immersed solid)功能是以浸入边界法为原理, 允许用户对一些涉及刚体对象穿过流体域的运动进行稳态或瞬态模拟。利用该功能, 可以不用进行几何重构和网格重新划分而获得将单个连续流体域分割成多个不连续流体域的流体仿真结果。而在以前的流体分析中, 一般要求计算的流体域是连续的, 即流体计算需要计算连续性方程。浸入实体功能可以以小幅牺牲精度为代价, 大大加快计算速度及计算稳定性。

1.2 方法验证

首先,需验证IBM数值方法的有效性。选取苏玉民等[2]在循环水槽中所进行的摆动尾鳍水动力性能研究试验作为对比对象, 对其模型进行数值仿真,最后比对数值结果与试验数据来验证方法。仿真模型如图1所示。模型特征弦长C0为0.3 m。针对外流场,通常认为上下游跨距超过10倍特征长度即可认为远场无扰动,侧向跨距超过5倍特征长度即可认为远场无扰动。因此,仿真的计算域取x轴方向(上下游方向)10倍弦长,在y轴方向取6倍弦长,在z轴方向取6倍弦长,外边界设置为压力远场边界,入口给定流速入口,出口给定压力出口边界,采用kω-SST湍流模型,最终的网格无关性网格数为300万。

图1 方法验证数值模拟模型Fig.1 Method validation numerical simulation model

通过ANSYS 流体动力学仿真软件(ANSYS CFX, CFX)中浸入实体功能对摆动尾鳍试验模型进行数值计算,得到一个周期内的推力系数Cx。将试验结果与数值模拟结果进行对比, 如图2所示。可以看出,模拟结果与试验数据曲线变化趋势大体一致,只在局部的波谷处有较大偏差。这是由于浸入边界法本质上是基于固壁边界附面层采用源项等效的一种近似,这种处理在层流及小分离流动时能达到较好的模拟精度,但当局部出现瞬时大分离流动时,由于湍流固有的结构复杂性和不确定性的加剧,此时单纯的源项是不足以准确近似湍流的,必然会出现较大数值偏差,但受主流区流动的制约,这种局部偏差有限,不会对流场发展趋势有质的改变,以其作为推进性能的定性判断还是可以作为参考的。因此,IBM方法对本文问题研究具有有效性。

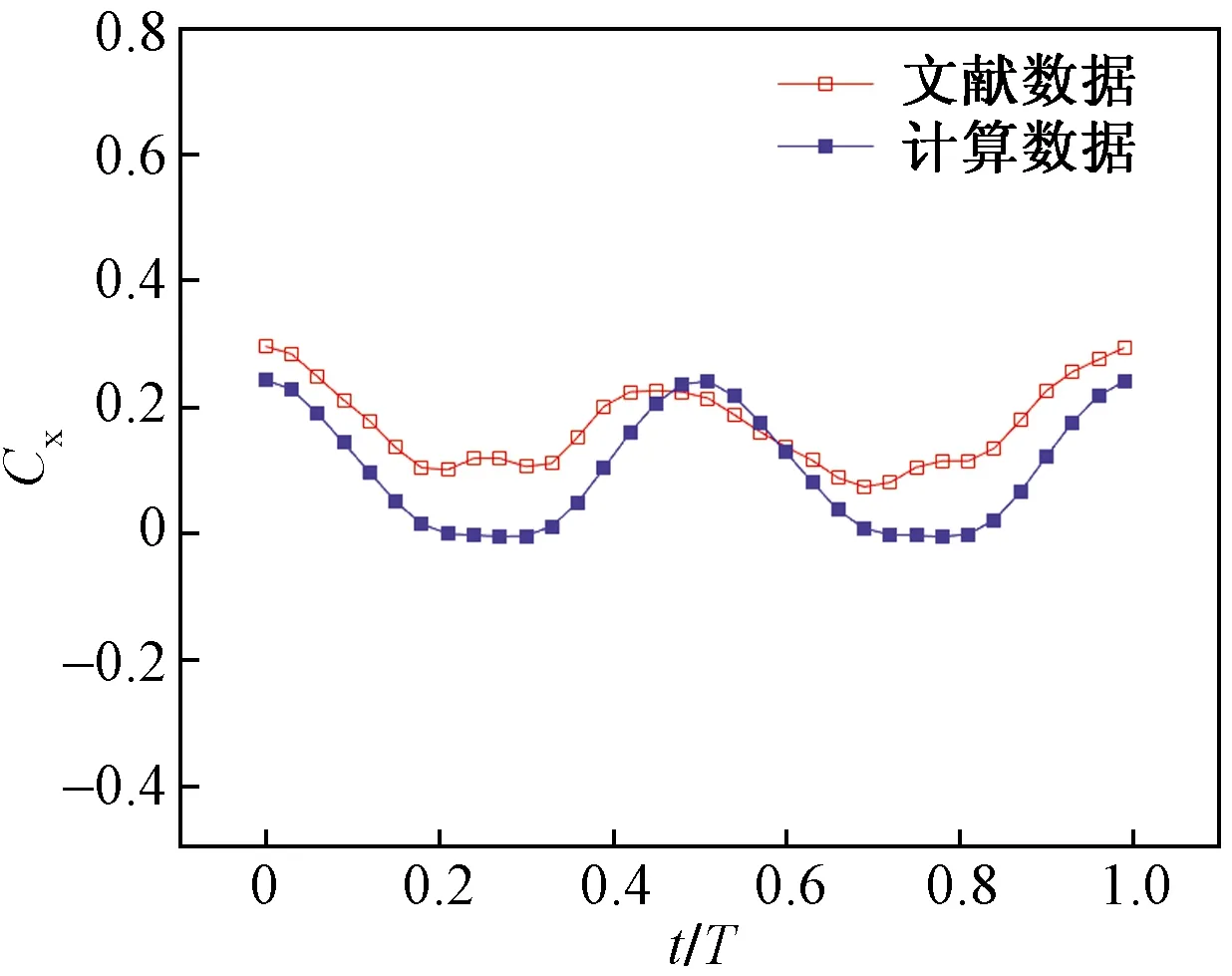
图2 计算结果与算例中试验结果比较Fig.2 Comparison of calculation results with test results in calculation examples

2 仿金枪鱼尾鳍几何建模

在新月形尾鳍外形参数方面, 根据陈宏[11]在设计一种金枪鱼外形的仿生机器鱼过程中, 通过最小二乘法对真实金枪鱼轮廓进行拟合得到的曲线公式对新月形尾鳍进行设计。根据其给出的公式, 可以得到本文中的新月形尾鳍曲线公式为

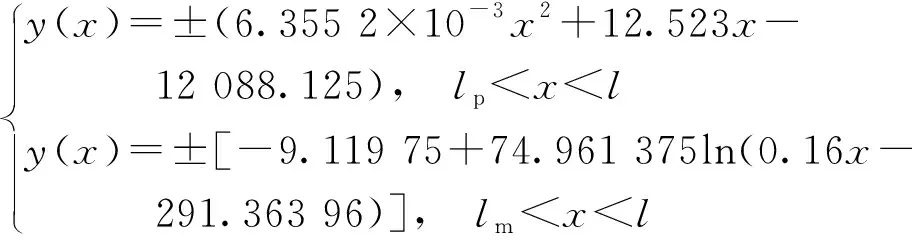
式(1)中:x为鱼体沿着体长方向坐标；y为鱼体沿着体高方向坐标；lp为尾柄最细位置到鱼头顶点位置的长度, 为1 700 mm；lm为鱼体在中心线上总长度, 为1 828 mm；l为鱼体全长, 为2 000 mm。

根据式(1)中给出的真实金枪鱼鱼体轮廓曲线函数, 可以得到金枪鱼垂直基准面外形轮廓线, 如图3所示。

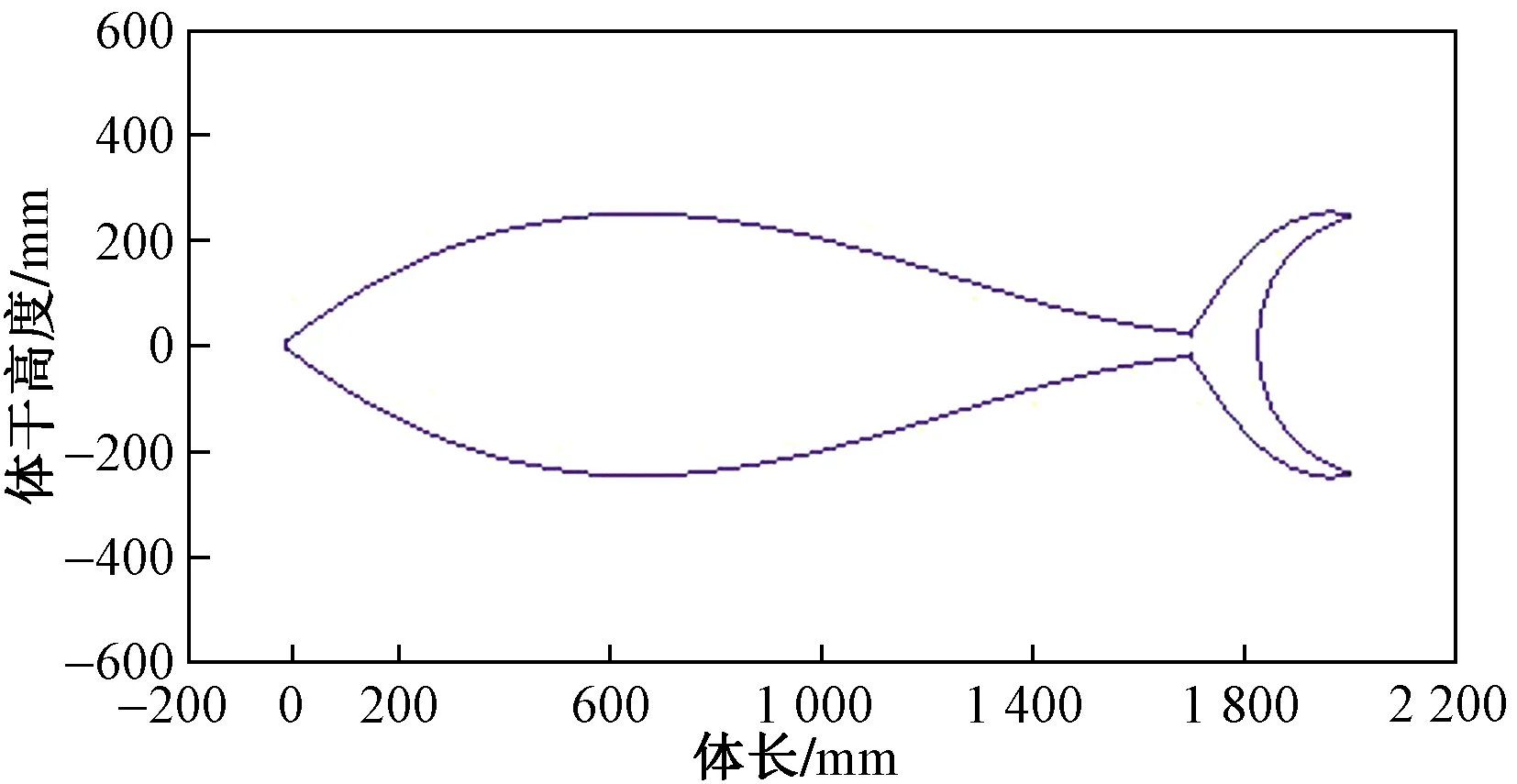
图3 金枪鱼垂直基准面轮廓线Fig.3 Vertical plane contour of tuna

根据上述金枪鱼体轮廓曲线函数, 对新月形尾鳍外形参数进行近似选择, 图4(a)所示为新月形尾鳍外形参数，其三维建模如图4(b)所示。根据式(1)进行计算, 选择并优化新月形尾鳍外形参数, 可以给出尾鳍长度lt为300 mm, 鳍梢长度lf为80 mm, 中弦长lc为128 mm, 后掠角α=47.4°, 展长b为242 mm。

在三维建模过程中, 根据新月形尾鳍形状及其主要参数建立模型, 同时新月形尾鳍的剖面翼型选择NACA0015系列翼型, 进行三维建模可以得到新月形尾鳍。

图4 新月外形参数及三维模型Fig.4 Lunate shape parameters and 3D model

3 仿金枪鱼尾鳍不同摆幅流场模拟

3.1 摆动尾鳍运动参数定义

对于以金枪鱼为代表的身体-尾鳍推进模式(body and/or caudal fin, BCF), 其主要推进力来自于后1/3部分。参照图5可以将尾鳍进行的复杂运动简化为以下3个简单运动。

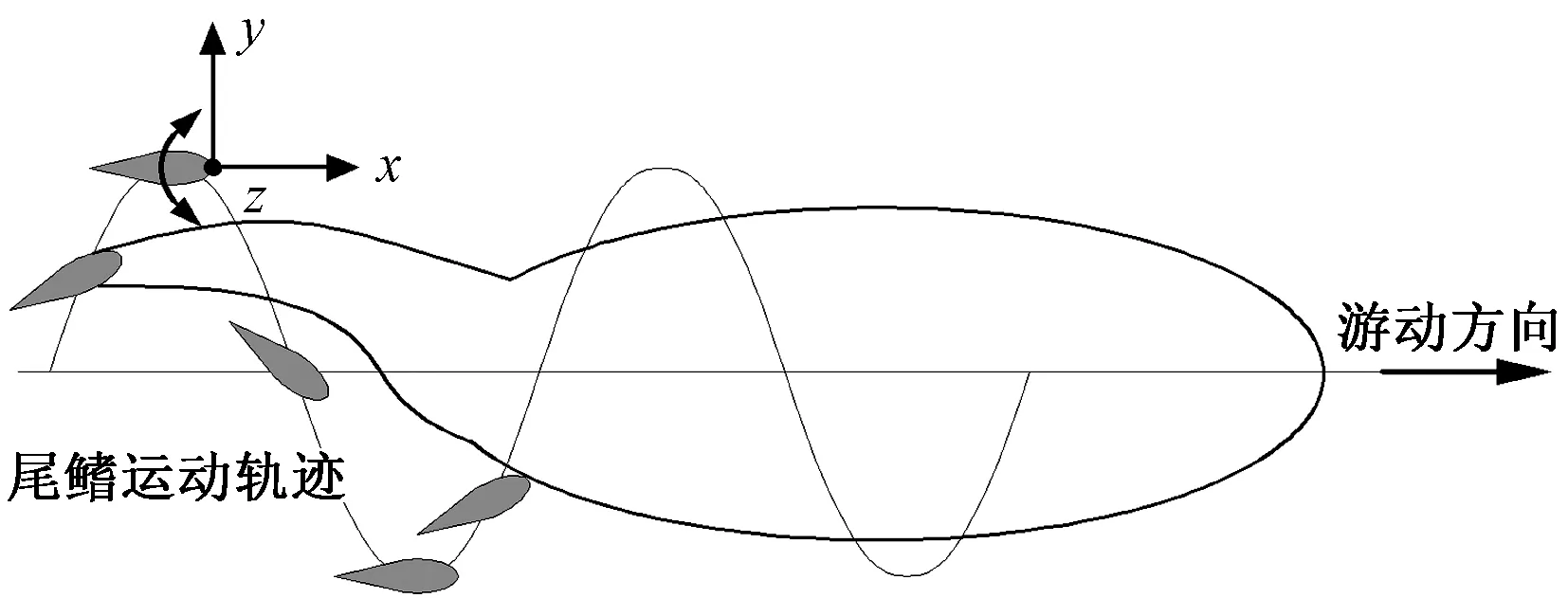
图5 金枪鱼尾鳍运动轨迹Fig.5 Movement track of a tuna-like caudal fin

(1)鱼在向前游动过程中, 尾鳍在X轴方向上及前进方向上产生的平动运动, 即巡航速度V0。

(2)尾鳍跟随鱼尾摆动进行的平动运动, 即升沉运动, 沿Y轴方向可表示为

y(t)=Asin(2πft) (2)

(3)尾鳍绕自身摆动轴的摆动运动, 即摇摆运动, 绕Z轴摆动的角位移可表示为

θ(t)=θ0sin(2πft-φ) (3)

式(2)、式(3)中:A为尾鳍的升沉运动的幅值,m；f为耦合运动的频率,Hz；θ0为尾鳍的摇摆运动幅度；φ为升沉运动和摇摆运动相位差。

对式(2)、式(3)进行求导, 可以得到尾鳍沿Y轴方向升沉运动的速度和绕Z轴摇摆运动的角速度分别为

V(t)=2πfAcos(2πft) (4)

ω(t)=2πfθ0cos(2πft-φ) (5)

3.2 水动力及相关系数定义

(1)对推进力进行无量纲化处理得到推力系数Cx,可以表示为

式(6)中:Fx为推进力,N；ρ为水的密度, kg/m3；S为尾鳍投影面积,m2。

(2) 斯特劳哈尔数Sr是影响摆动尾鳍推进性能重要的无量纲参数,表示为

Sr=fb/|V0| (7)

式(7)中:b为尾鳍运动过程中脱落尾涡的宽度, 近似表达为升沉运动幅值的2倍。

(3)摆动尾鳍的推进效率可以表示为

式(8)中:Cxm为平均推力系数,意义为Cx在一个周期内的平均值；Cy为侧向力系数；Cm为力矩系数。

3.3 变摆幅的数值模拟实现

根据计算数据进行三维建模, 分别用六面体、四面体对流域、尾鳍模型进行网格划分,计算模型与图1相似。通过浸入实体功能对刚体模型尾鳍穿过以水为介质的流体域的摆动过程进行模拟, 从而得到尾鳍在恒流, 即鱼在巡航状态下, 受到的推进力等相关参数。

改变尾鳍的摇摆运动幅度θ0, 使其依次为20°、25°、30°、35°,在这4种情况下对比分析摇摆运动幅度对尾鳍推进性能的影响。其余运动参数设置为周期T为1.6 s, 相位差φ为-50°, 尾鳍的升沉运动的幅值A为0.2 m,V0为0.3 m/s, 对应的Sr为0.4。

设置刚体尾鳍类型为浸入实体,选取计算时间为8 s, 时间步长为0.01 s, 选择刚体尾鳍运动方式为规定位移, 将其运动分解为平移与旋转进行设置。

4 结果与分析

基于浸入实体功能对尾鳍摆动运动进行仿真模拟, 得到压力分布、尾涡分布以及各个时刻的推进力大小, 并进一步获取推力系数以及效率。

4.1 尾鳍表面压力分布

图6所示是在θ0为20°的情况下, 尾鳍表面的压力分布云图。从图6中可以看出，尾鳍正面的压力分布与1/2周期后的背面压力分布基本相同,尾鳍正反两面从高压变为低压,再从低压转变为高压, 相互对应着按周期规律变化,由此可以看出尾鳍表面的压力分布是呈周期性规律进行变化的。

图6 尾鳍表面压力分布在一个周期内的变化Fig.6 Changes in pressure distribution on the surface of the caudal fin over a period

4.2 尾涡分布

尾鳍从最大振幅处向平衡位置摆动过程中, 由于尾鳍摆动形成的低压区会逐渐向尾鳍鳍尖处移动, 并最终脱落形成尾涡。这些从尾鳍上脱落下来的尾涡, 以反卡门涡街的形式进行排列, 使尾鳍后面的流场中流体呈喷射流动状态。在这些喷射流体的反作用下, 尾鳍获得向前的推进力。因此, 在尾鳍摆动产生推进力的过程中尾涡有着不可替代的重要作用。在三维流场中, 尾涡的形状和分布非常复杂, 通过ANSYS 流体动力学仿真后处理软件(ANSYS CFD-POST, CFD-POST)中提供的对物理量进行三维体积渲染可以直观地显示流场中的尾涡以及涡量强度。

尾涡涡量的体积渲染图图形遮盖严重, 这里取Z=0的平面进行对尾涡的观察分析。通过图7可以看出尾涡的脱落规律及涡量大小的变化。尾涡在尾鳍由最大振幅处向平衡位置摆动过程中形成, 故在一个运动周期内会脱落生成两次, 并在脱落后不断扩散, 涡量不断减小, 一周期内先后脱落的尾涡在尾鳍后按次序分布排列, 最终所有尾涡以反卡门涡街形式排列。

图7 一个周期内尾涡的变化Fig.7 Variation of wake vortex in a cycle

4.3 推进系数及推进性能影响

通过浸入实体功能可以计算得到仿金枪鱼尾鳍受到流体的作用力。数值计算后得到每个时间步下在尾鳍受到的推进力, 从而计算得到推进力系数变化如图8所示。推进系数Cx对摆动周期比t/T按照类正弦规律周期性变化, 随着摇摆幅度θ0增大, 其幅值也在不断变大, 因此增大摇摆幅度θ0, 使尾鳍与流体间作用力变大。

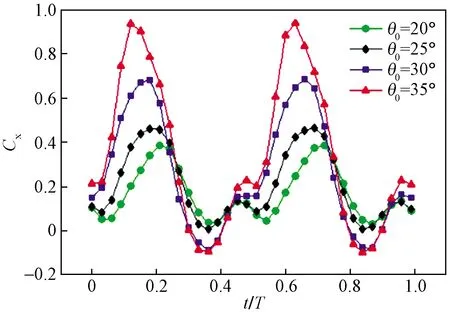
图8 一个运动周期内不同摇摆幅度下推进系数的变化Fig.8 Variation of propulsion coefficient under different swing amplitudes during a motion cycle

进一步对数据进行处理, 可以得到平均推力系数Cxm及效率η随摇摆幅度θ0变化曲线,如图9所示。平均推力系数Cxm随摇摆幅度θ0变大不断变大, 同时效率η随着摇摆幅度θ0变大不断变小。这表明随着摇摆幅度θ0的增加, 尾鳍产生的推进力变大, 但其推进效率不断下降, 这也符合鱼类启动过程中摆动幅度大、获得加速度大、但效率远低于巡航状态的特点。

图9 摇摆幅度对尾鳍推进性能的影响Fig.9 Effect of swing amplitude on the tail fin propulsion performance

5 结论

基于浸入边界法研究了仿金枪鱼尾鳍不同摇摆幅度θ0运动下的推进性能, 得到符合实际的结果。

(1)通过仿金枪鱼尾鳍运动一个周期内压力场云图、尾涡变化图, 分析了在摆动过程中尾鳍两侧压力的变化规律以及尾涡的变化规律;在Sr恒定的流场中, 推力系数曲线周期性变化, 呈类正弦曲线形状;随着摇摆幅度θ0的增加, 尾鳍产生的推进力变大, 但其推进效率不断下降。

(2)研究验证了IBM方法模拟尾翼非定常流动的有效性, 实现了仿金枪鱼尾鳍在流场中的复合运动进行模拟, 获取了尾鳍表面压力分布及尾涡涡量的分布,得到不同尾鳍摇摆幅度对推力系数及效率的影响差别, 提取了利于提高推进性能的摆幅影响规律,对仿金枪鱼尾鳍机构的设计和控制具有重要参考意义。