多尾鳍仿生航行器推进性能的三维数值研究

张智伟，易淼荣，敬 军，秦丰华，杨基明

（1．中国科学技术大学 近代力学系，安徽 合肥 230027；

2．中国船舶重工集团公司 第七○一研究所，湖北 武汉 430064）

多尾鳍仿生航行器推进性能的三维数值研究

张智伟1，易淼荣1，敬 军2，秦丰华1，杨基明1

（1．中国科学技术大学 近代力学系，安徽 合肥 230027；

2．中国船舶重工集团公司 第七○一研究所，湖北 武汉 430064）

采用格子波尔兹曼方法及浸没边界法，发展了一套适用于自由游动的三维数值研究程序。进而以多尾鳍推进仿生航行器为原型，讨论了尾鳍数目、形状、材料刚度等构型参数及振幅、频率等尾鳍摆动参数对推进性能的影响。结果表明对称布置、反对称摆动的双尾鳍能够明显消除侧向力而避免航行器主体的横向晃动，且推力大于两个单独尾鳍的简单加和；在中等Reynolds数下，具有波动性质的柔性尾鳍不论是推进速度还是推进效率均优于刚性尾鳍；当尾鳍单纯摆动推进时，具有完整鳍面的半椭圆形尾鳍的推进性能优于后部有缺口的深叉形尾鳍。

仿生航行器；双尾鳍；三维；推进性能

0 引 言

现代社会对资源的需求不断增加，海洋资源的探测与开发变得越来越重要。无人水下航行器（Unmanned Underwater Vehicle，UUV）是进军海洋的基本装备，提高其性能以适应复杂的环境、满足多变的任务需求，在军事和民用领域都是重要的研究课题。传统UUV多采用螺旋桨、喷流回旋式或者叶轮式等推进方式，但存在着推进效率低、机动性不佳等缺点，与水生动物优良的游动能力相比更是相形见绌。模仿鱼类游动方式，设计新型的仿生推进航行器，是开发高性能UUV的一条重要途径。

对于鱼类推进机理，人们进行了广泛的研究。先驱性的基础工作如Lighthill将空气动力学的二维机翼理论运用于尾鳍推进的研究，进而提出适用于鲹科推进模式分析的“大幅度细长体理论”［1］；吴耀祖将经典非定常振动翼理论扩展到二维柔性面推进，发展出“二维波动板理论”，首次讨论了鱼类的最佳推进方式［2］。近年来，随着实验及数值手段的发展，人们对各种鱼类展开了更细致的研究。Stambuis等使用PIV技术测量活体鱼游动的二维流场，分析了流场结构和速度、加速度分布特性［3］。Lauder等人借助DPIV对蓝鳍翻车鱼的胸鳍进行了观测，观测到推力的产生和涡的形成［4-5］。Walke研究了棘鱼胸鳍运动的动力学特性［6］。中国科大应用DPIV测量活鱼C型起动的流场结构，揭示了尾鳍特性对流场的影响作用［7］。Dong采用有限元法研究波动板周围的流场情况，发现波动板产生的尾涡与鱼体波动推进的尾涡类似［8］。国防科技大学采用Fluent动网格分析技术对MPF模式鱼类运动学和动力学方面进行了研究［9-10］。

在鱼类游动机理研究的基础上，人们研制出了多种新型水下仿生航行器［11］。但在这一过程中，仍有一些问题需要解决，如鱼类推进理论模型及对应推进方式游动算法研究［12］、仿生航行器推进、机动与稳定之间的关系［13-15］等。本文拟采用数值方法来模拟三维仿生航行器的自主游动，探讨推进方式对推进性能的影响，为新型仿生航行器的研制和优化奠定基础。

仿生航行器游动是典型的非定常、大变形动边界流动问题，传统的流固耦合方法会遇到网格实时更新、计算效率低下等困难。由Peskin等提出的浸没边界方法（Immersed Boundary Method，IBM）可在一定精度范围内简单有效的处理非定常动边界问题［16］，其核心是建立流固交界面上相互作用力计算模型，将运动边界替换为边界附近区域内的体积力作用，进而将流体运动与边界运动解耦求解。众多学者提出了多种模型，发展出浸没边界法的不同版本，其中由Goldstein等提出用“反馈法”可使流动在边界处自动满足无滑移条件［17］，且可以考察固体质量及质量分布的影响［18］，本文即采用这种方法以及并行性能良好的格子玻尔兹曼方法（LBM）研究UUV的游动特性，主要讨论尾鳍数目、形状、刚度以及摆动振幅、频率等对推进性能的影响。

1 数值方法

本文计算模型如图1所示，UUV由主体及尾鳍构成，推进机构为单尾鳍或者对称布置的双尾鳍（图1a），通过尾鳍的摆动，推动自己在无界静止流体中自主游动。主体为旋成体，其母线取自DARPA SUBOFF模型［19］：

其中x为离顶点的距离，R为母线与对称轴的间距。这里以主体总长度进行了归一化，后续计算中可根据需要设定主体长度并按比例缩放。尾鳍铰接于主体尾端，鳍面包含完整的半椭圆（图1b）和后部有缺口的深叉形（图1c）两种形状。半椭圆形长短轴比为4，用于模拟丰满尾鳍或模型试验中常见的平板尾鳍；后部有缺口的深叉形尾鳍源自鲤形目鱼类裂峡鲃。

图1 计算模型及尾鳍形状Fig.1 The model for calculation and fin′s shape

1.1 浸没边界法（IBM）

UUV的运动可以分成两部分：尾鳍的摆动以及整体的自主游动，前者相对主体预先给定，是UUV得以自主游动的源泉。由于UUV自主游动，其表面用Lagrange坐标X＝（s，τ）描述。浸没边界法的核心就是建立表面上与流体的相互作用力模型，本文采用反馈法［17］计算，即：

其中α、β是两个较大的正常数，U（X，i）＝d X／di是UUV表面的运动速度，Uib（X，i）是与表面相同位置的流体速度，通过流场速度插值得到：

其中δΔh（X）是Dirac Delta函数，Δh是网格尺寸。UUV在流体作用力下自主运动，该过程将UUV看作刚体的自由运动，本文采用四元数法计算其质心速度及转动角速度，进而更新表面位置X及速度U，具体求解这里不再赘述。

1.2 格子玻尔兹曼方法（LBM）

由于采用浸没边界法，将运动边界对流动的影响转换成体积力作用，流动即可在相对简单的欧拉网格上求解，这正好有利于发挥LBM的优势。考虑体积力的格子玻尔兹曼方程［20］：

其中τ是单松弛时间，fα是分布函数，feqα是平衡态分布函数，δi是时间步长，eα是离散速度，α表示不同的离散方向。本文采用D3Q15速度模型，相应的平衡态分布函数为：

其中权函数：

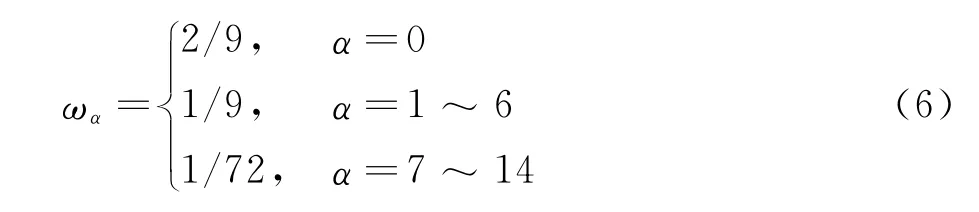
体积力模型采用郭照立等提出的GZS模型［21］：

其中，f是流体受到UUV的作用力：

宏观量密度与速度可由分布函数及体积力确定：

2 仿生航行器的数值模拟及参数分析

2.1 程序校验

为了校验程序，本文首先计算了压力驱动的三维Poiseuille流，其边界规则，不必采用浸没边界法处理，仅对流体计算程序即LBM部分进行验证。与三维Poiseuille流的精确解相比，计算所得流动结构完全一致。为进一步定量比较，图2给出了轴线上最大速度的计算误差，从图中可以看出误差大体上随Re增大而变大，Re接近1000时误差也不超过0．32%。

图2 Poiseuille流最大速度的相对误差（%）Fig.2 Relative error of the maximum velocity in Poiseuille flow（%）

为了进一步验证程序，计算了均匀来流中圆球绕流问题，在圆球表面采用浸没边界法处理。作为示例，图3（a）给出了Re＝100时xoy平面内的流线图，可以清楚的看到圆球下游的分离区。图3（b）给出了阻力系数随Re数的变化规律，可以发现与实验结果［22-23］完美相符。这表明本文程序是准确可靠的。

图3 圆球绕流Fig.3 Flow past a sphere

2.2 尾鳍摆动

尾鳍在摆动过程中，若鳍面始终保持为平面，则为刚性尾鳍，其摆动运动：

其中ηr表示沿鳍面距顶点ξ处偏离初始平面的距离，θm是尾鳍摆动的最大角度，T是摆动周期，φ0是初始相位，L是尾鳍长度，则最大摆动幅值Ar＝Lsin（θm）。当对称布置双尾鳍时，两尾鳍摆动仅初始相位相差π。若鳍面在摆动过程中呈现为非平面，则尾鳍为柔性的。本文研究中，不拟区分导致鳍面变形的原因，也即不区分其主动变形和被动变形，仅仅在确定的时刻给出鳍面的确切形状。鳍面形状采用Q．ZHU等通过观测拟合而得的结果［24］：

其中ηf是距顶点ξ处鳍面法向偏离初始平面的距离，λ是尾鳍柔性摆动波长，Am为常数，柔性尾鳍最大摆动幅值Af＝Am（c1L＋c2L2），其中c1＝0.002，c2＝-0．163。

由于LBM及IBM在Re数较小时精度更高，首先选取较小的Re数（这里为10）进行计算，后文再对Re数的影响进行讨论。对比分析四种半椭圆形尾鳍：刚性单尾鳍（以“r，s”标记）、刚性双尾鳍（“r，d”）、柔性单尾鳍（“f，s”）、柔性双尾鳍（“f，d”），各尾鳍摆动频率相同，最大幅值也相同，即Ar＝Af＝A。众所周知，鱼类尾鳍摆动推进时必然出现头部晃动的现象，即存在周期变化的侧向力。为此，图4（a）给出了一个摆动周期内侧向力Fy的变化，表明无论是柔性尾鳍还是刚性尾鳍，单尾鳍均产生了显著的侧向力，使主体有较大的侧向晃动，这与自然界的现象是一致的；而在双尾鳍推进方式下，由于两个尾鳍产生的侧向力时刻对称、相互抵消，侧向力为零，成功消除了主体的横向晃动，UUV得以稳定航行。由于本文中UUV自由游动，推力可由游动速度ui表示，如图4（b）所示，柔性尾鳍的推进速度显著高于刚性尾鳍；双尾鳍的推进速度比单尾鳍的两倍还高。注意到推力（或阻力）与速度二次相关，这表明双尾鳍产生的推力并不仅仅是两个单尾鳍的简单加和，其相互作用大大加强了双尾鳍的推进能力。

为了定量比较推进性能，定义平均推进速度：

以及平均消耗功率

其中F表示主体受到流场的作用力，u则表示对应点上主体的瞬时速度。四种尾鳍的推进性能如表1所示，柔性单尾鳍的的推进速度与刚性双尾鳍相当，但消耗的功率却与刚性单尾鳍相当；刚性尾鳍的推力峰值较高，从图4（b）也可以看出，刚性尾鳍的推进速度波动明显，换言之，刚性尾鳍推进过程中，加速度始终处于较高水平，较高比例的能量消耗于加、减速过程，导致推进效率很低。而柔性尾鳍的摆动具有波动性质，波动方向与推进方向相反，相对于刚性尾鳍，仅消耗一半的能量，推进速度却提高超过两倍。

表1 四种推进方式的速度、功率以及受力情况对比Table 1 The comparison of speed，power and thrust between four fins

2.3 尾鳍参数的影响

为了进一步分析并优化柔性尾鳍的推进性能，接下来讨论Re数、柔性尾鳍摆动波长λ以及尾鳍形状等参数的影响。

2.3.1Re数

为了方便，对所有的算例采用相同的参考长度L*和参考速度U*进行无量纲化，并由这些参考量定义Reynolds数：

其中ν*参考运动粘性系数。显然，参考量与具体的流动特征量有区别，但若参考量的选取合适，使得流动特征量为O（1）量级，则这里的Re数至少能部分的反映流动特征。刚性尾鳍的推进速度、功率与Re数的关系如图5所示。随着Re数的增大，粘性效应逐渐减弱，推进速度逐渐提高而消耗功率降低；当Re数足够大时，速度和功率仅随Re数缓慢变化。

图5 Re数对刚性尾鳍推进速度及消耗功率的影响（T=0.5，A=0.32，L=2）Fig.5 Effect of Re on the propulsion speed and power for rigid fin（T=0.5，A=0.32，L=2）

如前所述，即使尾鳍及尾鳍运动参数相同，不同Re数时推进速度也是不同的。图6（a）给出了两个周期内不同Re数时的瞬时速度，同样存在差异。若对每一个算例，均用流动的特征速度如UUV的平均游动速度重新无量纲化其瞬时速度，我们发现当Re数较大时，不同Re数时的瞬时速度曲线几乎完全重合，如图6（b）所示。这表明，在一定的Re数范围内，Re数对于尾鳍推进机理没有本质影响。当Re数较小时，如Re＜1，粘性作用将显著增强，推进机理则有本质变化。

2.3.2 尾鳍摆动参数

柔性尾鳍摆动具有波动性质，如式（12）所述。不同波长λ下的平均巡航速度和平均功率如图7所示。可以看出，巡航速度并不随波长单调变化，而在λ≈1.25L附近达到极大值；而消耗的功率却先减小后增大，在λ≈0.85L附近达到极小值。不难发现，波长越长柔性尾鳍越接近刚性摆动，而波长越短则波动性质越明显，鳍面变形越剧烈。不论是刚性摆动还是鳍面剧烈变化的波动摆动，尾鳍对流体的扰动都比较剧烈，消耗功率虽然较大但推进速度反而得不到相应提升。需要注意的是，这里的Reynolds数并不很高但也不很低，惯性效应的影响依然强烈，纯粹的波动推进并不像低Reynolds数下高效。另外，速度极大值与功率极小值对应的波长间稍有差别，这提示在实际使用柔性尾鳍时需要根据需求来选择合适的摆动方式。例如，在需要快速运动时选择波长比尾鳍稍长，而需要长时间巡航时则选择稍短的波长。

图6 不同Re数下的瞬时速度Fig.6 Instantaneous speed with different Reynolds number

图7 柔性双尾鳍平均巡航速度、消耗的平均功率随波长的变化（Re=10，T=0.5，A=0.32）Fig.7 Variation of the propulsion speed and power with the wave length for flexible double-fin（Re=10，T=0.5，A=0.32）

不同的摆动参数具有不同的推进性能，根据需求选择恰当的推进参数是一个重要问题。推进速度和消耗功率正是评价推进性能的两个重要参数，图8是双尾鳍各种摆动下的速度-功率曲线。在相同的速度下，消耗功率越低则推进性能越优秀。从图中可以看出，柔性摆动在所有情况下均优于刚性摆动，在本文参数下，柔性摆动的波长大约是尾鳍长度的1．25倍时推进性能是最优的；当推进速度较低时，不同尾鳍摆动参数对应的功率差别不大，调整摆动频率相对更优；当推进速度较高时，功率的差别也变明显，增加摆动幅度比增加频率所需能量更低。比较强的限制：鳍面绕根部纯转动。自然界中确实存在很多叉形尾鳍的鱼类，这类鱼游动时，并不是单纯依靠尾鳍摆动，身体后半部分也参与摆动推进。对尾鳍来说，其运动至少同时包含平动和转动两部分。自然界同样也存在翼或鳍仅转动的生物，如昆虫和某些淡水鱼类，这类生物的翼或鳍均是饱满的完整形状，后部并无叉形存在，也是一种相对较优的方式。

图8 双尾鳍功率-速度图Fig.8 Diagram of propulsion speed and power for double fin

2.3.3 尾鳍形状

在讨论尾鳍形状的影响时，两种尾鳍的鳍面面积相同。图9给出了摆动频率f＝2时刚、柔性双尾鳍的推进速度和消耗功率与摆动幅度的关系，柔性尾鳍的波长数λ＝1.5L，图中s1代表半椭圆形尾鳍，s2表示深叉形尾鳍。可以看出，两种尾鳍尽管形状不同，但变化趋势是一致的，而且消耗功率也是相当的，但更饱满的半椭圆尾鳍推进速度显著高于叉形尾鳍，柔性叉形尾鳍的推进速度甚至比刚性半椭圆尾鳍还低。速度-功率曲线更清楚的表明叉形尾鳍的推进能力非常有限。需要注意的是，这里对尾鳍的运动方式做了

图9 尾鳍形状对推进速度、功率的影响Fig.9 Effect of the fin shape on the propulsion speed and power

3 结 论

本文联合应用浸没边界法和格子Boltzmann方法，数值模拟了三维仿生航行器的自推进游动，结果表明：

（1）对称布置且反对称摆动的双尾鳍能显著消除侧向力，避免摆动推进的本体横向晃动问题；双尾鳍之间的相互作用还能提高推进速度，推力高于两个单独尾鳍的简单加和。

（2）具有波动性质的柔性尾鳍，相对刚性尾鳍更优，能显著提高推进速度而不需要额外的能量消耗；本文参数范围内，最优的摆动波长大约为1．25倍尾鳍长度；增加摆动频率和幅度均能提高推进速度，但消耗功率也同步增长。当需要的推进速度较低时，提高摆动频率而降低摆动幅度将降低消耗功率；而要求较高速度巡游时，则提高摆幅优于增加摆动频率。

（3）当尾鳍单纯摆动推进时，完整的、饱满的鳍面形状不论在推力还是效率方面均具有明显的优势。

［1］LIGHTHILL M J．Aquatic animal propulsion of high hydromechanical efficiency［J］．Journal of Fluid Mechanics，1970，44：265-301．

［2］WU T Y T．Hydromechanics of swimming propulsion．Part 1：swimming of 2-Dimensional flexible plate at variable forward speeds in an inviscid fluid［J］．Journal of Fluid Mechanics，1971，46：337-355．

［3］STAMHUIS E J，VIDELER J J．Quantitative flow-analysis around aquatic animals using laser sheet particle image velocimetry［J］．Journal of Experimental Biology，1995，198（2）：283-294．

［4］LAUDER G V，MADDEN P G A，MITTAL R，et al．Locomotion with flexible propulsors：I．experimental analysis of pectoral fin swimming in sunfish［J］．Bioinspiration&Biomimetics，2006，1（4）：S25-S34．

［5］DRUCKER E G，LAUDER G V．Locomotor forces on a swimming fish：three-dimensional vortex wake dynamics quantified using digital particle image velocimetry［J］．Journal of Experimental Biology，1999，202（18）：2393-2412．

［6］WALKER J A．Dynamics of pectoral fin rowing in a fish with an extreme rowing stroke：the three spine stickleback（Gasterosteus aculeatus）［J］．Journal of Experimental Biology，2004，207（11）：1925-1939．

［7］JING J，YIN X Z，LU X Y．Observation and hydrodynamic analysis on fast-start of yellow catfish（Pelteobagrus fulvidraco）［J］．Progress in Natural Science，2005，15（1）：34-40．

［8］DONG G J，LU X Y．Numerical analysis on the propulsive performance and vortex shedding of fish-like travelling wavy plate［J］．International Journal for Numerical Methods in Fluids，2005，48（12）：1351-1373．

［9］YANG S B，HAN X Y，BIAN W J，et al．Simulation of swimming of fish flapping pectoral fins［J］．Computer Aided Engineering，2006，S1：109-112．（in Chinese）

杨少波，韩小云，卞文杰，等．胸鳍摆动式鱼类的泳动仿真［J］．计算机辅助工程，2006，S1：109-112．

［10］HU T J，SHEN L C，GONG P L．CFD validation of the optimal arrangement of the propulsive dorsal fin of gymnarchus niloticus［J］．Journal of Bionic Engineering，2006，3（3）：139-146．

［11］YU J Z，CHEN E K，WANG S，et al．Research evolution and analysis of biomimetic robot Fish［J］．Control Theory & Applications，2003，4：485-491．（in Chinese）

喻俊志，陈尔奎，王硕，等．仿生机器鱼研究的进展与分析［J］．控制理论与应用，2003，4：485-491．

［12］JIANG X S．An overview of the prospects of robot technologies［J］．Robot，1996，5：285-291．（in Chinese）

蒋新松．未来机器人技术发展方向的探讨［J］．机器人，1996，5：285-291．

［13］BARRETT D，GROSENBAUGH M，TRIANTAFYLLOU M．The optimal control of a flexible hull robotic undersea vehicle propelled by an oscillating foil［C］．Symposium on Autonomous Underwater Vehicle Technology，1996：1-9．

［14］MORGANSEN K A，DUIDAM V，MASON R J，et al．Nonlinear control methods for planar carangiform robot fish locomotion［C］．IEEE International Conference on Robotics and Automation，2001，134：427-434．

［15］IIJIMA D，YU W W，YOKOI H，et al．Obstacle avoidance learning for a multi-agent linked robot in the real world［C］．IEEE International Conference on Robotics and Automation，2001：523-528．

［16］PESKIN C S．The immersed boundary method［J］．ACTA Numerica，2002，11：1-39．

［17］GOLDSTEIN D，HANDLER R，SIROVICH L．Modeling a noslip flow boundary with an external force-field［J］．Journal of Computational Physics，1993，105（2）：354-366．

［18］QIN F H，HUANG W X，SUNG H J．Simulation of small swimmer motions driven by tail／flagellum beating［J］．Computers&Fluids，2012，55：109-117．

［19］GROVES N C，HUANG T T，CHANG M S，Geometric characteristics of DARPA SUBOFF models（DTRC model Nos．5470 and 5471）［R］．David Taylor Research Center Ship Hydrodynamics Department，DTRC／SHD-1298-01，1989．

［20］WU J，SHU C．An improved immersed boundary－Lattice Boltzmann method for simulating three-dimensional incompressible flows［J］．Journal of Computational Physics，2010，229（13）：5022-5042．

［21］GUO Z L，ZHENG C G，SHI B C．Discrete lattice effects on the forcing term in the lattice Boltzmann method［J］．Physical Review E，2002，65（4）：046308．

［22］REN A L，LI G W，ZOU J F．Numerical study of uniform flow over sphere at intermediate Reynolds numbers［J］．Journal of Zhejiang University（Engineering Science），2004，38（5）：644-648．（in Chinese）

任安禄，李广望，邹建峰．中等雷诺数圆球绕流的数值研究［J］．浙江大学学报（工学版），2004，38（5）：644-648．

［23］TANEDA S．Experimental investigation of the wake behind a sphere at low Reynolds numbers［J］．Journal of the Physical Society of Japan，1956，11（10）：1104-1108．

［24］ZHU Q，WOLFGANG M J，YUE D K P，et al．Three-dimensional flow structures and vorticity control in fish-like swimming［J］．Journal of Fluid Mechanics，2002，468：1-28．

Proposion performance of three-dimensional biomimetic underwater vehicle

ZHANG Zhiwei1，YI Miaorong1，JING Jun2，QIN Fenghua1，YANG Jiming1
（1.The University of Science and Technology of China，Hefei 230027，China；2.China Ship Development and Design Center，Wuhan 430064，China）

A numercial code for 3-dimensional fluid flow around swimming bodies were developed．The Immersed Boundary method（IBM）was applied to characterize the moving and deformable fluid-body interface in terms of a momentum forcing so that bodies′motion and fluid flow were uncoupled．The fluid flow was solved by Lattice Boltzmann method（LBM）which was well suited to be parallelized and the body motion was devided into beating which was pre-specified and swimming which was calculatied according to the resultant forces and moments．Then，the self-propulsion of a biomimetic unmanned underwater vehicle（UUV）with multiple fins was simulated，and the effects of fins′properties and of beating parameters on the propulsion performance were discussed in detail．It was shown that the lateral force generated by symmetric double fins almost vanished，and the trust was enhanced where the vehicle cruise speed was larger than twice the speed by single fin．UUV propelled by flexible fins swam much faster than that by rigid ones．Under the condition of present work，the optimized wavelength of the flexible fin is about 1．25 times the fin length，and the vehicle swam faster with lager beating amplitude or with higher frequency．The propulsion performance of Semi-oval-shaped caudal fin was better than that of deeply forked tail fin when the vehicle paraded with low speed．

biomimetic underwater vehicle；double fin；three-dimensional；propulsion performance

V211.3

Adoi:10.7638／kqdlxxb-2013.0022

0258-1825（2014）05-0634-07

2013-02-28；

2013-06-11

国家自然科学基金（11272310）；中国舰船研究设计中心B类研发基金（YFB11-04-35）

张智伟（1989-），男，硕士研究生，主要从事计算流体力学工作．E-mail：zzhiwei＠mail．ustc．edu．cn

秦丰华（1975-），男，博士，副教授，主要从事仿生学、微流体力学等领域工作．E-mail：qfh＠ustc．edu．cn

张智伟，易淼荣，敬军，等．多尾鳍仿生航行器推进性能的三维数值研究［J］．空气动力学学报，2014，32（5）：634-640．

10．7638／kqdlxxb-2013．0022．ZHANG Z W，YI M R，JING J，et al．Proposion performance of three-dimensional biomimetic underwater vehicle［J］．ACTA Aerodynamica Sinica，2014，32（5）：634-640．