基于双向流固耦合仿真的新月形尾鳍水动力学特性研究
葛飞飞, 沈 灿, 谢 鸥
(苏州科技大学 机械工程学院, 江苏 苏州 215009)
随着地球上陆地资源逐渐枯竭,人类对海洋资源的开发已经迫在眉睫。 在复杂的海洋流场环境下,传统的螺旋桨推进水下机器人的稳定性和工作效率都不高,各种推进效率高的仿生机器鱼成为研究人员的重点研发对象[1-3]。
根据鱼类的外形特征和游动方式不同,可将鱼类分为两种:身体/尾鳍(BCF)推进模式和中央鳍/对鳍(MPF)推进模式[4-5]。 自然界中约80%的鱼类采用BCF 推进模式,其具有游动速度快、推进效率高等特点,目前已成为研究者进行仿生工程研究的重要对象。 BCF 推进模式主要依靠鱼体的后半部分和尾鳍摆动产生推进力,尾鳍在鱼类推进过程中发挥着重要作用。
研究表明鱼类尾鳍的刚度、形状和摆动相位等会对其水动力参数产生显著影响。 王志东等[6]通过数值计算,研究了金枪鱼游动及其尾鳍摆动的二维模型,讨论了刚性和柔性尾鳍的不同水动力性能。 Luo 等[7-8]提出一种双向流固求解器对刚度非均匀分布的尾鳍进行了仿真分析,结果表明刚度非均匀分布的尾鳍能有效模拟真实鱼类的尾鳍变形特征。 章永华等[9-10]利用计算流体动力学原理,给出了尾鳍表面压力分布和无量纲阻力系数变化情况,结合尾鳍不同切面涡结构,揭示了通过在尾鳍表面设置漏空区域调节推进力的规律。
本文旨在研究新月形仿生机器鱼尾鳍的结构参数和运动参数对其水动力参数的影响。 基于双向流固耦合仿真技术,建立了新月形仿生机器鱼尾鳍摆动模型,重点讨论了新月形尾鳍在不同运动参数、不同刚度、不同厚度以及不同面积下的水动力学特性,为仿生机器鱼尾鳍设计提供指导。
1 数值计算
1.1 仿真建模
建立如图1(a)所示长方体的计算区域,左侧为速度入口,右侧为压力出口,来流速度设置为0.5 m/s,且尾鳍的展长为300 mm,尾鳍弦长和尾柄长度共计为150 mm。 壁面及尾鳍表面设置为无滑移壁面条件,采用六面体结构化网格对计算区域进行划分,如图1(b)所示,并对尾鳍周围的网格进行局部加密,采用动网格技术处理尾鳍的动边界问题。

图1 仿真模型
基于仿真模型的坐标系XYZ,定义无量纲推力系数Cx、无量纲侧向力系数Cy及其相应的无量纲平均推力系数和无量纲平均侧向力系数如下:
其中,Fx(t),Fy(t)分别表示推进力和侧向力,ρ 表示流体密度,V 表示来流速度,S 表示尾鳍的迎水面面积,T 表示摆尾周期,t 表示时间。
尾鳍按照正弦规律进行拍动,其运动学方程如下
其中,α(t)指不同时刻的拍动角度;α0指初始时刻角度偏移,本文为设置为0;A 为摆角幅度;f 为摆动频率;α1为初始时刻相位偏移,其值设置为0。 在仿真计算中,摆角幅度设置为10°、20°和30°。
1.2 控制方程
在双向流固耦合数值计算中,流体域的求解需满足质量守恒、动量守恒、和能量守恒三大定律,相关方程如下
式中,i,j=1,2,3;ρ 为流体密度;P 为压强;μ 为动力黏度;α 为热扩散系数。 本文数值计算中湍流模型选择RNG k-ε 模型,该湍流模型具有良好的分离流计算性能,其k 方程和ε 方程如下k 方程:
ε 方程:
其中,C1、C2、σk、σε均为经验常数。
固体域求解涉及的方程如下
耦合交界面处的数据传递所满足的方程如下
其中,下标f 代表流体域参数,下标s 代表固体域参数。
2 仿真结果分析
2.1 尾鳍摆角幅度对水动力参数的影响
图2 所示为尾鳍摆角幅度对水动力学参数的影响关系。 尾鳍的材料选择PE(聚乙烯),其杨氏模量和泊松比分别为5E8 Pa 和0.42。 尾鳍的运动频率设置为f=1 Hz,表面积设置为S=260 cm2,摆角幅度分别设置为10°、20°和30°。
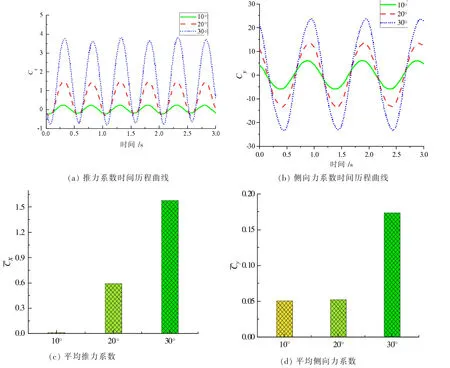
图2 尾鳍摆角幅度对水动力参数的影响关系
由图2(a)和图2(b)可知,推力系数曲线和侧向力系数曲线均呈周期性波动,且推力系数曲线的波动频率是侧向力系数曲线的2 倍。 随着摆角幅度增大,推进力系数曲线和侧向力系数曲线的波动幅值均呈增大趋势变化。进一步,由图2(c)和图2(d)可知,随着摆角幅度的增大,平均推力系数呈快速增大趋势变化,而平均侧向力系数在摆角幅度小于20°时变化很小,达到30°时明显的增大。此结论表明,增大尾鳍摆角幅度可有效提高推进力,同时也带来了游动的不稳定性。
2.2 尾鳍摆动频率对水动力参数的影响
图3 所示为尾鳍摆动频率对水动力参数的影响关系。 尾鳍的材料选择PE,摆角幅度为30°,表面积S=260 cm2,摆动频率分别为0.5、0.8 和1 Hz。
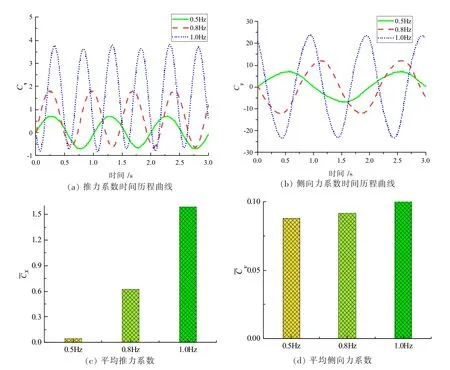
图3 尾鳍摆动频率对水动力参数的影响关系
由图3(a)和图3(b)可知,推力系数曲线和侧向力系数曲线的幅值随尾鳍摆动频率呈增大趋势变化。 同理,由图3(c)和图3(d)可知,平均推力系数和平均侧向力系数也随频率呈增大趋势变化。说明增大摆动频率可提高推进力,同时也增大了侧向力。
2.3 尾鳍厚度对水动力参数的影响关系
图4 为尾鳍厚度对水动力参数的影响关系。选取等厚度和连续变厚度两种尾鳍进行仿真分析,其中连续变厚度是指从尾柄到尾鳍后缘,尾鳍的厚度逐渐减小,从而使尾鳍的刚度也连续变小。尾鳍的材料选择PE和结构钢,其中结构钢的杨氏模量和泊松比分别为2E11 Pa 和0.3。 尾鳍的摆角幅度为30°,表面积S=260 cm2,摆动频率f=1 Hz。

图4 尾鳍厚度对水动力参数的影响关系
选取等厚度和连续变厚度两种尾鳍进行仿真分析,其中连续变厚度是指从尾柄到尾鳍后缘,尾鳍的厚度逐渐减小,从而使尾鳍的刚度也连续变小。 由图4(a)和图4(b)可知,变厚度PE 尾鳍的推力系数曲线幅值明显大于其它三种尾鳍,同时,变厚度尾鳍的侧向力系数曲线的幅值比等厚度尾鳍大。 对于同种材料,由图4(c)可知,变厚度尾鳍的平均推力系数要大于等厚度尾鳍,且PE 尾鳍的平均推力系数更大。 相反,变厚度尾鳍的平均侧向力系数比等厚度尾鳍小(见图4(d))。 以上结果表明,变厚度柔性尾鳍具有更好的推进性能,此结论符合真实鱼类尾鳍结构的特征。
2.4 尾鳍刚度对水动力参数的影响
图5 所示为尾鳍刚度对水动力参数的影响关系。本文选取三种不同的尾鳍材料:PE、PC(聚碳酸酯)和结构钢,其中聚碳酸酯的杨氏模量和泊松比分别为2.32E9 Pa 和0.39。 尾鳍运动频率为f=1 Hz,表面积S=260 cm2,摆角幅度为30°。

图5 尾鳍刚度对水动力参数的影响关系
由图5(a)和图5(b)可知,PE 尾鳍的推力系数曲线和侧向力系数曲线的幅值明显大于PC 和结构钢尾鳍。 进一步,由图5(c)和图5(d)可知,PE 尾鳍产生的推进力优于PC 和结构钢尾鳍,而PC 尾鳍产生的侧向力明显大于其他两种尾鳍。 以上结果表明,柔性尾鳍(PE 尾鳍)的推进性能更好。
图6 所示为结构钢尾鳍和PE 尾鳍在一个摆尾周期内的压力云图。 对比分析两种尾鳍产生的压力云图可以看出,PE 尾鳍上下两面所形成的正压或者负压与结构钢尾鳍相比,前者均大于后者。 在t=0.25T 和t=0.75T这两个时刻时,PE 尾鳍相较于结构钢尾鳍,前者摆动幅度与尾柄处变形大于后者,两种尾鳍表面所形成的负压以及尾部脱落的涡也是前者较大。 上述结果表明柔性尾鳍(PE 尾鳍)的流程压力变化更大。
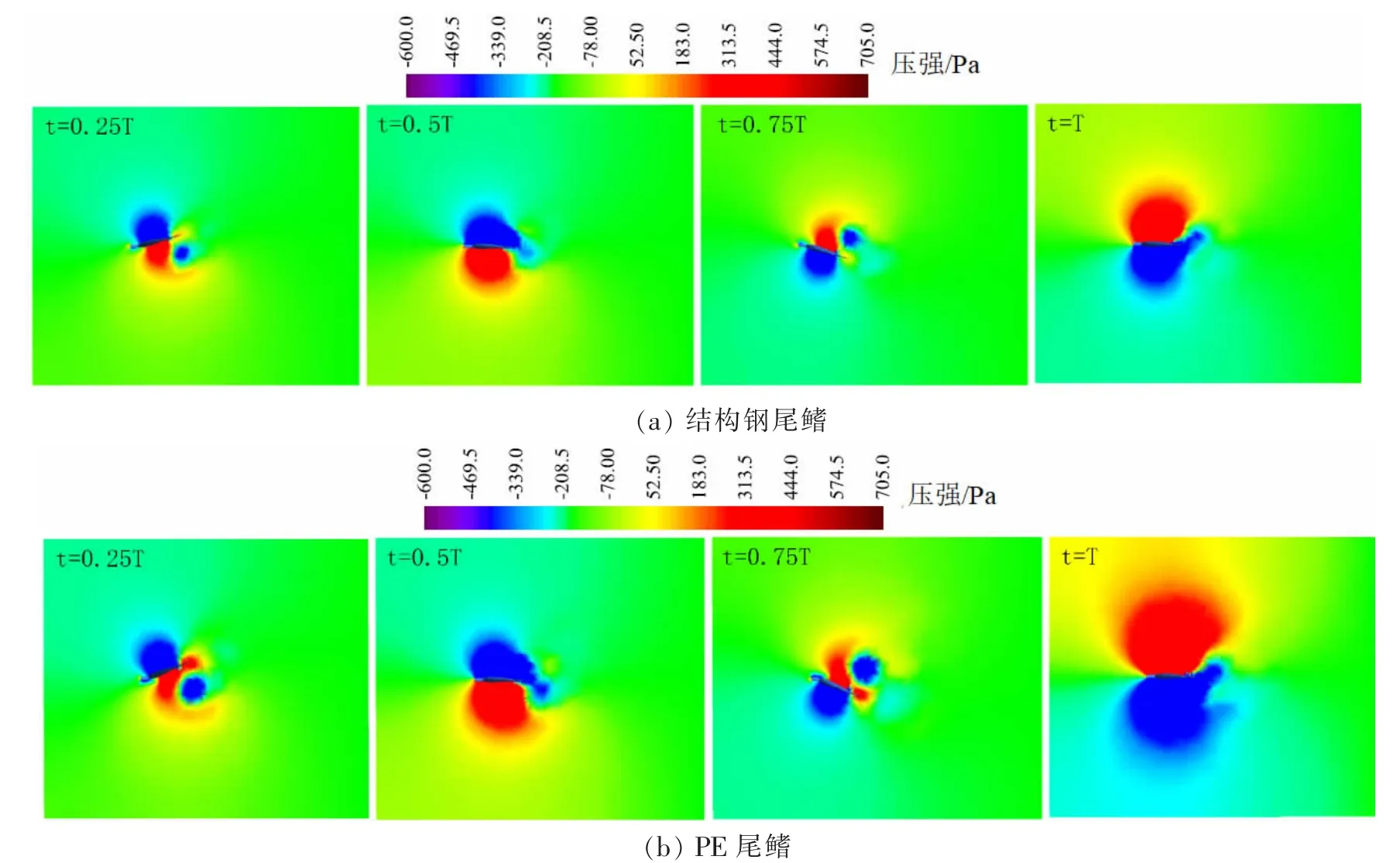
图6 压力云图
2.5 尾鳍面积对推进性能的影响
进一步,本文研究了尾鳍面积对推进性能的影响关系。 如图7 所示,保持尾鳍的翼展不变,从尾鳍后缘增加弦长中心线方向的长度从而获得不同的尾鳍面积。 本文对4 种不同面积的尾鳍进行了仿真计算,尾鳍面积分别设置为S1=180 cm2,S2=220 cm2,S3=260 cm2,S4=300 cm2。

图7 尾鳍面积变化示意图
图8(a)和图8(b)所示分别为尾鳍在0.5 Hz 和1 Hz 的摆动频率下,3 种不同材料尾鳍(PE、PC 和结构钢)的平均推力系数随面积变化的曲线,且尾鳍摆角幅度设置为30°,尾鳍面积设置为S=260 cm2。
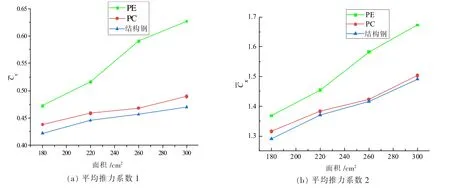
图8 尾鳍面积对推进性能的影响
由图8(a)和图8(b)可知,不论摆动频率为0.5 Hz 还是为1 Hz,3 种不同材料尾鳍的平均推力系数均随尾鳍面积呈单调递增趋势变化, 而且对于给定的四种面积,PE 尾鳍的平均推力系数明显大于其它两种尾鳍,而PC 尾鳍的平均推力系数略大于结构钢尾鳍。同时从图8可以看出,对于同种材料的尾鳍,频率越大,尾鳍产生的推进力越大。 以上结果表明,尾鳍面积越大、摆动频率越高的柔性尾鳍产生的推进力越大。
3 结论
本文从数值计算角度出发,采用双向流固耦合计算方法,研究了新月形仿生机器鱼尾鳍的水动力学特性。得到如下结论:(1)增大尾鳍摆角幅度可有效提高推进力,同时也带来了游动的不稳定性;(2)增大尾鳍的摆动频率可提高推进力,同时也增大了侧向力;(3)柔性尾鳍(PE 尾鳍)的推进性能相较于刚性材料尾鳍更好;(4)变厚度柔性尾鳍相较与等厚度柔性尾鳍而言,具有更好的推进性能,符合真实鱼类尾鳍结构特征;(5)尾鳍面积越大、摆动频率越高的柔性尾鳍产生的推进力越大。

