目标函数误差估算及网格自适应处理

杨夏勰，周春华

（1．南京航空航天大学 空气动力学系，江苏 南京 210016；2．上海飞机设计研究院飞控部，上海 201210）

目标函数误差估算及网格自适应处理

杨夏勰1，2，周春华1

（1．南京航空航天大学 空气动力学系，江苏 南京 210016；2．上海飞机设计研究院飞控部，上海 201210）

发展了一种基于目标函数误差估算的网格自适应准则，进而通过网格自适应处理提高目标函数计算的效率和准确性。首先描述了目标函数的误差估算及修正的方法，该方法通过伴随方程将原方程的残值误差与目标函数联系起来。然后，基于误差估算建立网格自适应准则，以减少目标函数修正后的剩余误差，提高目标函数计算结果的准确性，并将方法进一步发展至多目标问题。最后将该准则应用于Euler方程控制的NACA0012翼型无粘可压流动的网格自适应模拟。数值计算成功地捕获了与升力、阻力和力矩等目标函数相关的特征流动区域，计算出符合指定精度要求的目标函数值，验证了本文所发展的方法。

误差估算；目标函数修正；伴随方程；网格自适应处理

0 引 言

网格自适应处理是提高流动数值模拟效率和准确性的有效手段之一。如何建立可靠的自适应准则是网格自适应处理的关键问题之一。通常采用的自适应准则可分为两类：（1）物理量的梯度；（2）离散解的误差估算值。前者不可避免地会遗漏部分信息，在解决多变量问题时存在一定困难；而且在变量大梯度区域进行连续的网格加密也不能保证总体误差一定同时下降。后者通常是从方程的解出发，计算比较困难。对复杂非线性问题，如Navier-Stokes方程，难以提出严格的误差估算器。

另外一种思路是：不对流动方程数值解的误差进行估算，而直接对工程应用中感兴趣的积分输出量（即目标函数，如飞行器设计中的升力、阻力等气动力参数）进行误差估算。基于这种误差估算的网格自适应处理可提高指定输出量的准确性。以往的基于误差估算的自适应是针对流动方程的解本身。提高整个流场的精度也能提高目标函数的精度，但相比而言不是直接的，效率上要低一些。而基于目标函数误差估算的方法则完全以提高目标函数的准确性为目标，对目标函数敏感区域的网格将被优先加密，针对性更强，更适合于工程设计中的应用。近年来，在双曲型问题、不可压N-S方程和可压Euler方程中运用伴随方法对目标函数进行误差估算的研究已经取得了一些进展［1-4］。在许多工程计算中，目标函数的误差是设计人员最优先考虑的因素，而采用伴随方法的意义就在于伴随解可以看作是目标函数关于流动解线性化的影响。在误差分析中，通常用残值误差来衡量数值近似解与原始偏微分方程精确解之间的误差程度，而残值误差又与流动解相对应。因此，伴随解加权了残值误差对目标函数的影响［5-6］。在那些伴随变量很小的区域，较大的残值误差对目标函数的影响很小，网格就不需要加密；相反，在伴随变量较大的区域，即使很小的残值误差对目标函数的影响也可能很大，所以就需要局部网格加密。基于这种误差估算所发展的自适应方法先在有限元法中得到发展［7］，最近在有限体积法中也有应用［3］。

本文以Pierce和Giles［8-9］及Venditti和Darm of al提出的方法［10］为基础，发展了一种目标函数的误差估算和修正技术以及相应的网格自适应准则；减少了计算量，提高了目标函数的准确性，并进一步将之推广到多目标问题。首先给出了基于伴随方程的误差估算及修正过程。在这个过程中并不需要求解细网格上的流动解，只计算细网格上的目标函数值和残值误差，以及粗网格上的伴随解。然后给出了自适应方法，其目的是通过局部加密粗网格以降低剩余误差从而提高目标函数的计算精度。上一次加密形成的细网格作为当前迭代的粗网格，这个过程反复进行直到收敛。收敛的定义是局部误差达到一个期望值。最后，本文针对二维无粘可压流问题进行了数值实验，目标函数选择航空工程应用中最感兴趣的升力、阻力和力矩等系数。计算结果验证了所发展方法在提高目标输出量准确性方面的可靠性。这种自适应准则更加适合工程应用，其重要性是不言而喻的。

1 目标函数的误差估算及修正过程

首先，简单讨论基于伴随方程的目标函数的误差估算和修正［11-12］。考虑两套不同的网格：粗网格ΩH和细网格Ωh。记ΩH、Ωh上的目标函数值分别为fH（uH）、fh（Uh），其中UH、Uh分别代表粗、细网格上偏微分方程的离散解。直接在细网格上求解偏微分方程获得fh（Uh）的时间代价肯定很大。通过对fH（UH）修正而近似获得fh（Uh）是值得期待的。

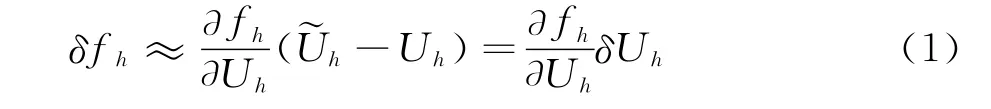
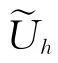
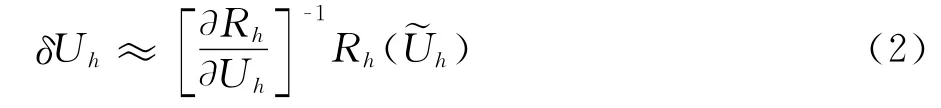
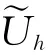
其中Ψh是下列细网格上伴随方程的离散解：

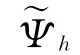
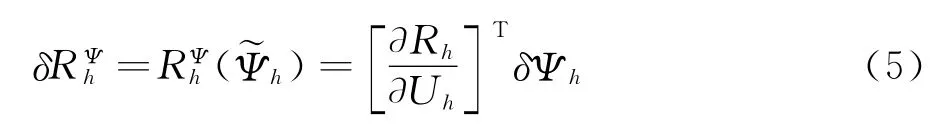
最后由式（3）和式（5）获得目标函数的误差：

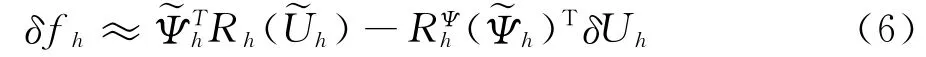
2 网格自适应准则

这一节我们给出一种网格自适应方案来完善上一节给出的目标函数的修正。网格自适应处理的目标是减少式（6）中的剩余误差，即减少目标函数修正后的剩余误差。

2.1 修正后的剩余误差

由式（6）可得，目标函数的误差可以表示成可计算修正项与剩余误差项之和。剩余误差可以写成不同的形式。式（6）中剩余误差是伴随方程残值的误差与原方程解的误差的内积；它也可以表示成伴随解的误差与原方程残值的误差的内积［13］。因此，目标函数误差也可写成下列形式：

网格自适应的目标就是减少式（6）和式（8）中两种形式的剩余误差，以提高修正后目标函数的精确度。显然，自适应参数应包含两种形式的剩余误差。

2.2 自适应准则和参数

我们希望通过网格自适应处理，减少计算域内的自适应参数的值，即降低目标函数修正后的剩余误差。记粗网格单元k内的细网格节点集为l（k），k的自适应参数εk可以定义为：

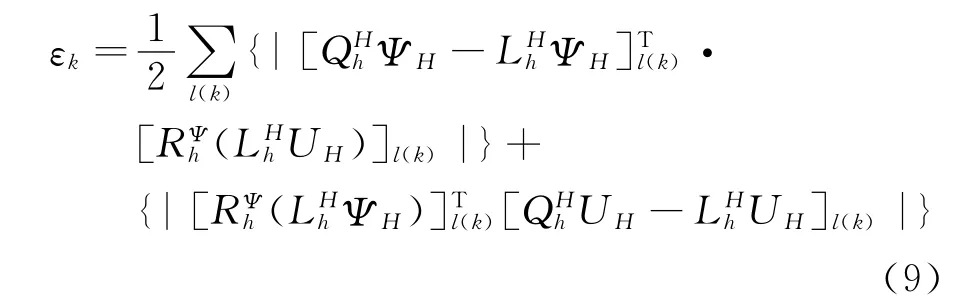
2.3 多目标的网格自适应处理

上述的误差估算与网格自适应都是对单个目标函数值进行的，这种方法也可用于同时处理多个目标函数。每一次求解流动方程后，根据不同的目标函数分别求解对应的伴随方程，从而获得对应的自适应参数。这样，每个网格就有多个剩余误差，即每个目标函数对应一组剩余误差和自适应参数。当有一个剩余误差大于目标误差时，该单元就加密；即只有当所有剩余误差都小于对应的目标误差时，该单元才不需要加密。同时处理多个目标函数的优势在于只需要求解一轮流动控制方程。从后面的数值实验可以看到，多目标函数的精确度与单目标几乎一样。

3 数值方法

本节简单介绍Euler方程和伴随方程的数值求解方法。

3.1 Euler方程求解

空间离散采用有限体积median-dual格点格式［14］，控制体形状如图1所示。控制体上的积分形式的Euler方程为：

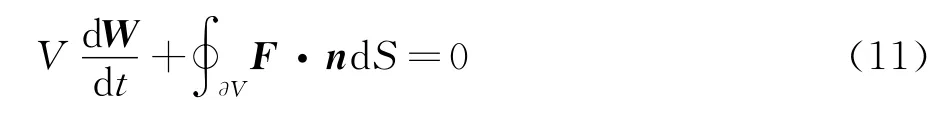
其中V为控制体的体积，W表示守恒变量，F为对流通量矢，∂V表示控制体的边界，n是边界的单位外法向矢量。对流通量离散采用中心格式近似，人工粘性项由拉普拉斯算子和双调和算子混合构成，时间推进采用五步龙格库塔格式。

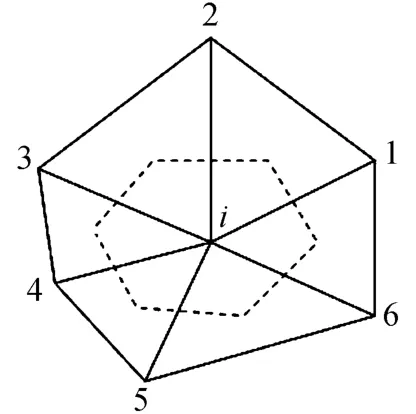
图1 节点i的控制体Fig.1 Control volume of node i

3.2 伴随方程求解

如第一、二节所述，为了进行目标函数的修正及网格自适应参数的计算，获得流动方程的解后就需要求解如下粗网格上的伴随方程：

其中Ψ表示粗网格上的伴随解，R表示Euler方程的残值，f表示目标函数。

伴随方程的数值解法与Euler方程类似，可以采用龙格库塔时间推进的方法来获得伴随解。

本文选择工程领域比较感兴趣的升力系数、阻力系数和俯仰力矩系数为目标函数。∂R／∂W、∂f／∂W的计算可参考有关气动外形优化的文献［14］；限于篇幅，其计算这里不再详述。

3.3 插值算子

为了获得粗网格上的流动解和伴随解在细网格上的映射，采用多项式插值函数作为三角形单元上的插值算子。对于二次插值，多项式可以表示为：

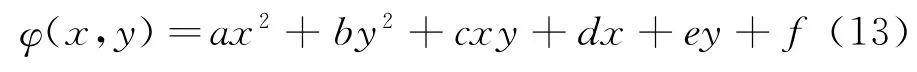
这里，a～f是待定系数。为了求得六个未知系数，需要在粗网格上的六个节点建立六个方程。这里，取图2所示的六个粗网格节点。待定系数确定后，将细网格上节点i的坐标（xi，yi）代入（13），即可获得i点上的任意变量的值φ（xi，yi）。

图2 粗网格节点：1-6，细网格节点：PFig.2 Coarse-mesh nodes：1-6，fine-mesh node：P

4 数值模拟及讨论

我们对NACA0012翼型无粘可压绕流进行数值模拟，验证所发展的误差修正和网格自适应处理方法的可靠性和有效性。

4.1 M∞=0.95，α=0°，目标函数为阻力系数

该流场中，翼型紧靠前缘处有脱体激波，后缘处有两道附体激波且其下游还有一弱正激波。图3和图4分别给出了期望误差e0＝0.01和e0＝0．0005时的自适应网格和计算结果。两种情况都是自适应加密两次后，所有单元满足误差要求ηk＜1，对应网格节点分别为1774和4802。从图3（a）和图4（a）中我们可以看到，自适应网格中后缘斜激波和下游的正激波处网格未被加密，说明这两处激波对阻力计算的影响不大。图3（b）和图4（b）给出了多层均匀网格的结果、自适应网格的结果以及修正后的自适应结果；可以看出，满足精度要求的自适应解经修正后非常接近外插值，而且网格规模很小。外插值是根据Richardson法获得的，选取的三个外插点是最后三层均匀加密网格上的阻力系数值。对比不同期望误差的结果图可以看出，期望误差越小，网格加密越多，获得的目标函数值越趋近于外插值。

表1给出了自适应网格和均匀加密三次的网格上节点数目、误差估算值和计算时间的对比。可以看出，自适应网格上目标函数的总体误差估算值和计算时间都远远小于均匀网格。

表1 自适应网格与均匀网格上的计算Table 1 Computations on adapted and uniform grids

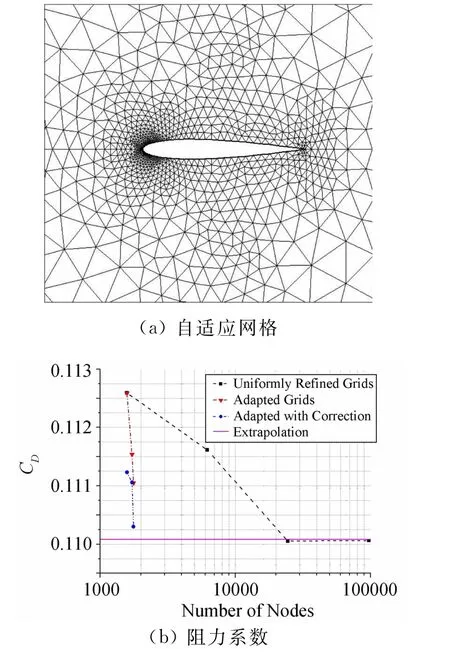
图3 M∞=0.95，α=0°，e0=0.01时的自适应网格和阻力系数Fig.3 Adapted grid and drag coefficients for M∞=0.95，α=0°，e0=0.01

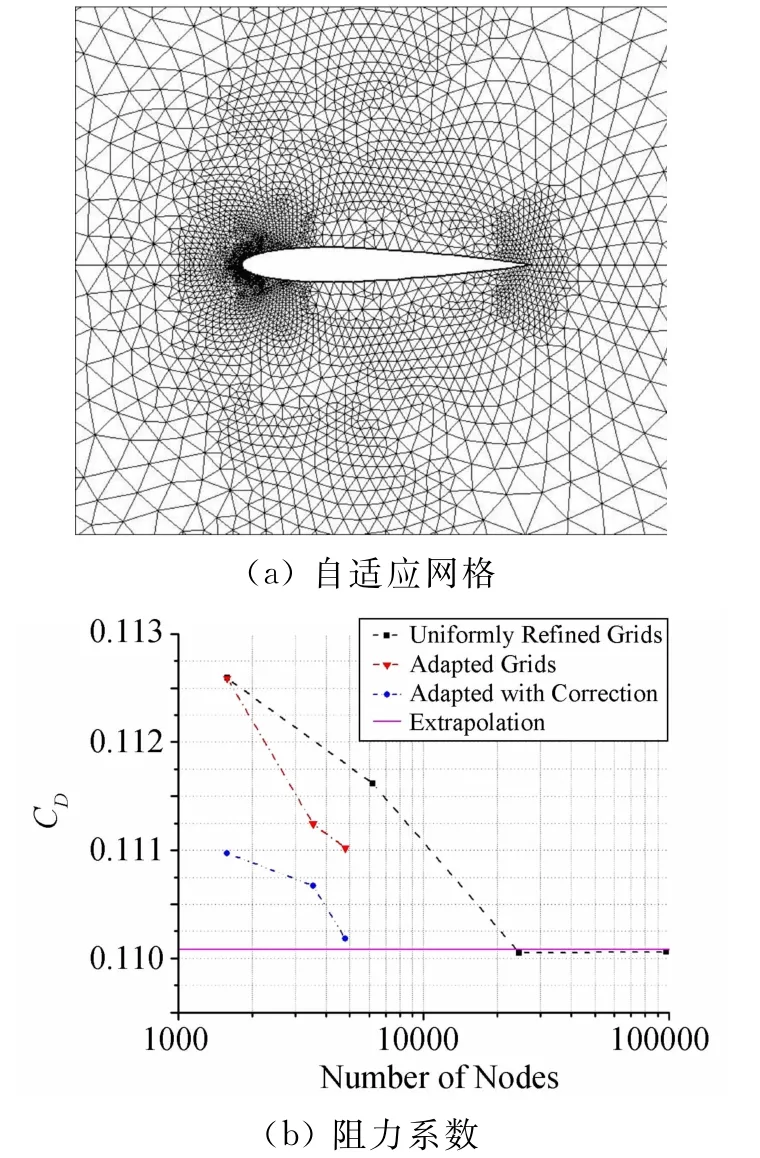
图4 M∞=0.95，α=0°，e0=0.0005时的自适应网格和阻力系数Fig.4 Adapted grid and drag coefficients for M∞=0.95，α=0°，e0=0.0005

4.2 M∞=0.8，α=1.25°，目标函数为力矩系数

图5给出了期望误差e0＝0．01时的自适应网格和计算结果。自适应加密四次后，所有单元当地误差满足ηk＜1，最终网格节点数为3504。外插值同样是根据均匀加密网格上的结果获得。从网格加密图中可以看出，翼型前后缘和上激波对力矩系数的误差影响较大。通过所采用的自适应准则及误差修正后，目标函数值能较好地趋近外插值。参照文献［15］，图5（b）也给出了基于压强梯度加密的力矩系数结果。通过对比可以看到，采用本文方法所得到的结果值更加接近于外插值，目标函数值更加准确。

4.3 M∞=3，α=0°，双翼型，目标函数为下翼型的阻力系数

从图中翼型的安放位置可以看出，上游翼型的激波会影响下游翼型。图6给出了期望误差e0＝0．001时的自适应结果。自适应加密三次结束，网格节点数为4766。从网格加密图中可以看到，下翼型网格加密主要集中在前缘和前缘斜激波；上翼型网格加密集中在前缘及下表面的斜激波。说明这些区域对于目标函数的误差影响比较大。两个翼型的尾激波都没有加密，说明这些区域的流动对目标函数的影响较小。

4.4 M∞=0.8，α=1.25°，目标函数为升力系数和阻力系数

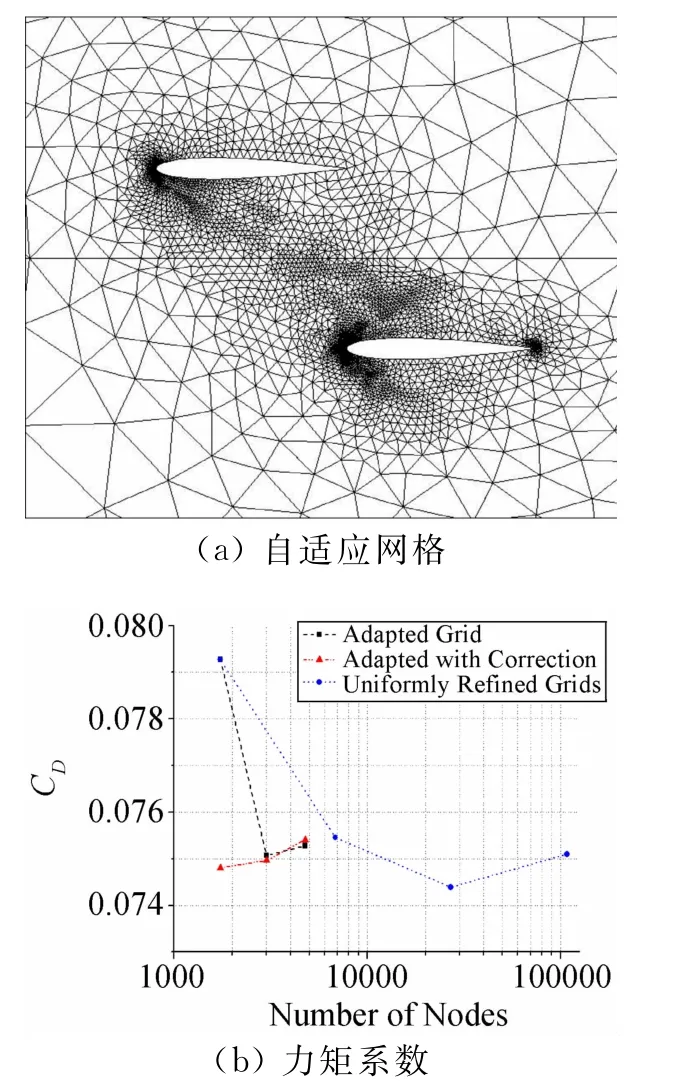
图6 M∞=3，α=0°，e0=0.001时的自适应网格和阻力系数Fig.6 Adapted grid and drag coefficients for M∞=3，α=0°，e0=0.001

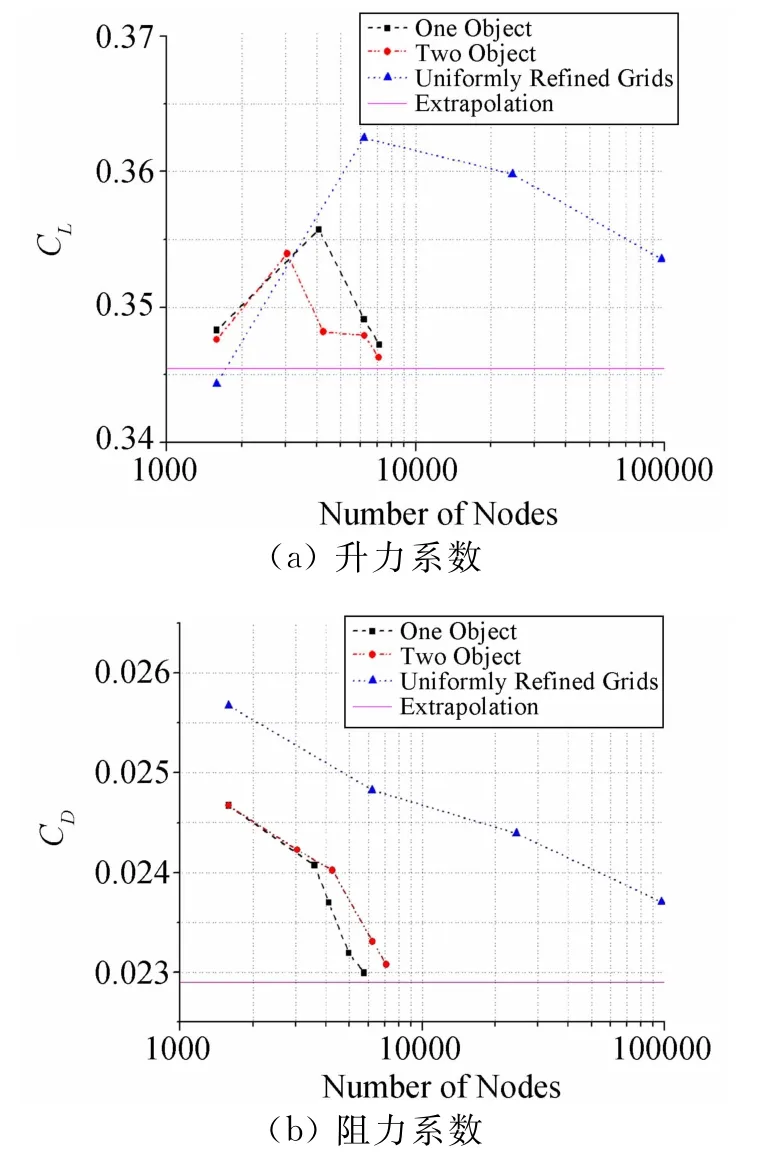
图7 M∞=0.8，α=1.25°时的升力系数和阻力系数Fig.7 Lift and drag coefficients for M∞=0.8，α=1.25°

这一小节给出了双目标函数的网格自适应处理结果，并且与单目标情形进行了比较。图7（a）给出了目标函数为升力系数、阻力系数和同时为升力系数及阻力系数的网格自适应计算结果。期望误差分别为ecl＝2．5%CL，ecd＝0．001。双目标函数加密四次后自适应结束，网格节点为7102。单目标函数升力系数加密三次结束，网格节点7003；阻力系数加密四次结束，网格节点5751。图中可以看到，双目标函数的计算结果与单目标函数几乎一样，同时处理两个目标函数也能保证相同的计算精度。但是在程序运行上，双目标函数少解了一轮求解流动控制方程，大大减少了计算时间。图8给出了双目标函数的网格加密图，在翼型前后缘、上下激波处都有适当的加密，表面这些区域对升力系数、阻力系数这两个目标函数的计算精度有较大的影响。

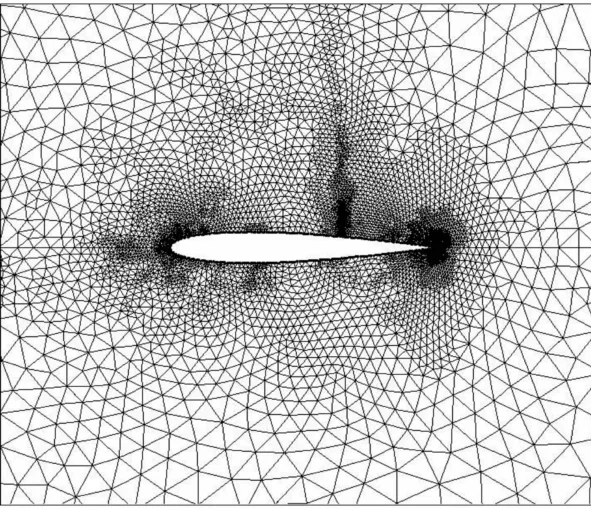
图8 M∞=0.8，α=1.25°双目标自适应网格Fig.8 Adapted grid with two objects for M∞=0.8，α=1.25°

5 总结与展望

本文基于目标函数的误差估算及修正技术，发展了一种网格自适应处理方法，以提高升力系数、阻力系数和力矩系数等指定积分输出量（即目标函数）的准确性。对NACA0012翼型无粘可压流的数值实验表明：自适应参数很好地捕获了那些对目标函数误差影响较大的区域，通过对这些区域的网格加密，提高了目标函数值的准确性。在所给出的算例中，目标函数都达到了要求的精度，网格自适应处理因而具有自动终止的特点；而且满足精度要求的自适应解经修正后非常接近均匀网格结果的外插值。本文还将单目标函数的网格自适应方法扩展到双目标函数的情形。数值实验结果表明：双目标情形下，计算精度依然获得很好的满足，但计算时间大大减少。在未来的工作中，我们将对随时间变化的流动问题做进一步的研究和分析。时间相关的模拟中总体误差可以分解为空间误差、时间误差，以及每个物理时间步内虚拟时间迭代不完全收敛带来的误差（针对通常采用的双时间步格式）。如果将时间域与空间域分开单独考虑，这三种误差的伴随方程与定常问题应该是相似的，处理起来或许不太困难。如果将空间自适应与时间自适应耦合起来，尚有不少问题有待解决。

［1］PARASCHIVOIU M，PATERA A．A posteriori finite element bounds for linear-functional outputs of elliptic partial differential equations［J］．Comput.Methods.Appl.Mech.Engrg.，1997，150：289-312．

［2］RICHARD P D．Heuristic a posteriori estimation of error due to dissipation in finite volume schemes and application to mesh adaptation［J］.Journal of Computational Physics，2008，227：2845-2863．

［3］MANI K，MAVRIPLIS D J．Error estimation and adaptation for functional outputs in time-dependent flow problems［J］．Journal of Computational Physics，2010，229：415-440．

［4］BECKER R，RANNACHER R．A posteriori error control in finite element methods［J］．Tech.Rep.University at Heidelberg，1994．

［5］PARK M A．Adjoint-based three-dimensional error prediction and grid adaptation［R］．AIAA 2002-3286，2002．

［6］SULI E．A posteriori error analysis and adaptivity for finite element approximations of hyperbolic problem［A］．Lecture Notes in Computational Science and Engineering［C］．Heidelbeig：Springer，1998：123-194．

［7］GILES M B，LARSON M G，LEVENSTAM M，et al．Adaptive error control for finite element approximations of the lift and drag in a viscous flow［R］．Technical Report，NA 97／06，1997．

［8］PIERCE N A，GILES M B．Adjoint recovery of super-convergent functional from PDE approximations［J］．SIMA Rev．，2000，42（2）：247-264．

［9］GILES M B，PIERCE N A．Adjoint equations in CFD：duality，boundary conditions and solution behavior［R］．AIAA 97-114，1997．

［10］VENDITTI D，DARMOFAL D．Adjoint error estimation and grid adaptation for functional outputs：application to quasi-onedimensional flow［J］．Journal of Computational Physics，2000，164：204-227．

［11］BALASUBRAM R，NEWMAN J C．Comparison of adjointbased and feature-based grid adaptation for functional outputs［J］．Numer.Meth.Fluid，2007，53：1541-1569．

［12］BALASUBRAM R．Error estimation and grid adaptation for functional outputs using discrete-adjoint sensitivity analysis［D］．Mississippi State University，2002．

［13］GILES M B，PIERCE N A．An Introduction to the adjoint approach to design［J］．Flow Turbulence and Combustion，2000，65：393-415．

［14］AMOIGNON O．Adjoint-based aerodynamic shape optimization［R］．［IT Licentiate Theses］．Tech．Report，2003-012，2003．

［15］YANG Z H，ZHOU L．Output-based error estimation and grid adaptive mesh refinement［J］．Aeronautical Computing Technique，2011，41（3）：14-16．（in Chinese）

杨振虎，周磊．基于误差估计的伴随网格自适应方法［J］．航空计算技术，2011，41（3）：14-16．

Output-based error estimation and grid adaptation

YANG Xiaxie1，2，ZHOU Chunhua1
（1.Department of Aerodynamics，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China；2.Department of Flight Control，Shanghai Aircraft Design and Research Institute，Shanghai 201210，China）

A mesh-adaptation criterion using output-based error estimation is developed to improve the accuracy of the output and the efficiency of computations．At first，the procedure of output-based error estimation and correction are described．Primal residual error and prescribed functional are related to each other by the adjoint method．The discrete adjoint solution is a weighting function，which weights the primal residual error．The error estimation and correction needn′t to compute the flow and adjoint solution on the fine mesh，which will be obtained by prolongation operation．Then，a strategy for grid adaptation is developed to reduce the remaining error after the functional correction and improve the accuracy of computations．Furthermore，the mesh adaptation method is extended to multi-object problems．The adaptation parameter is the remaining error，which contains both primal residual error and adjoint residual error．The governing equations are two-dimensional Euler equations．They are solved by using finite volume approximation and five-step Rungge-Kutta temporal discretization．The adjoint is a discrete equation and its solution procedure is similar to that of governing equations．Finally，the strategy is applied to the simulation of inviscid compressible flows around the NACA0012 airfoil．Numerical experiments have successfully captured the features which are associated with the prescribed functional，produced integral outputs with desired accuracy，and finally validated the method developed in this article．

error estimation；functional correction；adjoint；mesh adaptation

O335；V211.3

Adoi:10.7638／kqdlxxb-2012.0189

0258-1825（2014）05-0688-06

2012-11-13；

2013-03-09

国家自然科学基金（11072113）；江苏高校优势学科建设工程资助项目

杨夏勰（1987-），女，助理工程师，研究方向：网格自适应处理．E-mail：kathryn711＠126．com周春华（1965-），男，教授，博士生导师，研究方向：计算流体力学，数值分析等．E-mail：chzhou＠nuaa．edu．cn

杨夏勰，周春华．目标函数误差估算及网格自适应处理［J］．空气动力学学报，2014，32（5）：688-693．

10．7638／kqdlxxb-2012．0189． YANG X X，ZHOU C H．Output-based error estimation and grid adaptation［J］．ACTA Aerodynamica Sinica，2014，32（5）：688-693．