观三线 抓特点 辨八角

赵连杰

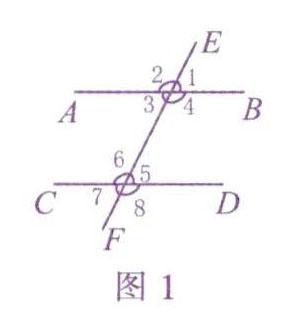
两条直线被第三条直线所截.构成了八个角，我们习惯上称之为“三线.八角”.

如图l所示，其中没有公共顶点的角可分为三类，即同位角、内错角、同旁内角，它们是进一步学习平行线的判定和性质的重要基础，是学好本章的关键所在.但因这三个概念近似，同学们辨别起来有很大困难，经常出现这样那样的错误.现对辨别这三个概念的步骤说明如下，希望对同学们有所启示，

第一步：确定截线与被截线

辨别“三线八角”的关键是确定哪两条直线被哪一条直线所截，为此首先要分清两条直线和第三条直线，为了直观简便，可以将两条直线称为被截线，将第三条直线称为截线，截线是被截两条直线的桥梁.确定它们的方法为：待確定的两个角分别有一条边在同一条直线上，那么这条直线就是截线，两个角另外两条边所在的两条直线就是被截线，或者说，截线是同位角、内错角或同旁内角中两个角的一边所在的公共直线，两条被截线是同位角、内错角或同旁内角中两个角的另一条边所在直线.

第二步：抓住每个概念的特征

1.同位角要抓住一个“同”字，即“位置相同”，其意思是两个角都在截线的同旁和两条被截线的同方向（同上或同下，同左或同右）.

2.内错角要抓住“内”字和“错”字，即夹在两条被截线之间和位于截线的两旁，形同“Z”.

3.同旁内角要抓住“同”字和“内”字，即夹在两条被截线之间和位于截线的同旁，形同“U”.

第三步：准确得出结论

结合图形，根据第一步的方法确定截线和被截线后，根据第二步中各个概念的特点（主要就是看要判断的角与前面确定的截线和被截线的位置关系），给出结论，对于比较复杂的图形，要善于将图形分解，即根据自己所思考的问题，抽出只与所考察的角有关的直线或线段，去掉那些与问题无关的直线或线段（也就是留下第一步确定的相关的两条被截线和一条截线），从而得到正确的结论.

几个应该特别注意的事项：

1.三类角反映的是角与角之间的位置关系而不是数量关系，因此，不论被截的两条直线是否平行，都存在上述三类角.

2.对于比较复杂的图形，可以用不同颜色的笔将所找到的截线和被截线描出来，然后再辨别是哪一类角.

3.注意与前边学过的对顶角、邻补角的区别，这三类角没有公共顶点.

例l 如图2所示.∠B和∠FAC是哪类角？∠B和∠C呢？

解析：8 ∠B的两边分别在直线AB，BC上，∠FAC的两边分别在直线AB，AC上，所以AB为截线，BC，AC为被截线，∠和∠FAC都在截线AB的同旁和被截的两直线BC，AC的同方向（上方），由此便知∠B和∠FAC为同位角.

∠B的两边分别在直线AB，BC上，∠C的两边分别在直线BC，AC上，所以BC为截线，AB，AC为被截线，∠B和∠C都在截线BC的同旁和被截的两直线AB，AC之间，由此便知∠B和∠C为同旁内角，

练一练

1.如图3所示，下列说法错误的是（  ）.

A.∠l与∠A是同旁内角

B.∠3与∠A是同位角

C. ∠2与∠3是同位角

D.∠3与∠B是内错角

2.下列四个图形中，∠1与∠2为同位角的是（  ）.

参考答案：1.B 2.D