把握相交与平行

孔凡哲

“相交线与平行线”是图形与几何的基本内容.在本章中，我们将在已有知识与经验的基础上，继续研究两条直线的位置关系，在学习中，我们不仅要了解补角、余角、对顶角以及它们的性质，而且要掌握平行线的特征以及判别两直线平行的条件，同时，我们将进一步探索相交与平行的秘密，积累几何活动经验，培养几何直观，提高推理能力。

一、生活中的平行线

我们的生活中处处可见相交线和平行线，诸如，棋盘上的横线和竖线，道路上的斑马线，文具盒的相邻两边，操场上的双杠等，

其实，生活中处处离不开平行线.窗户上下边框是平行的，保证玻璃窗能顺利被推拉：拉紧的电线之间是相互平行的，这样既美观又能保证安全，

二、全面理解平行的含义

教科书中把“在平面内，两条不相交的直线”叫作平行线，这里的不相交是指永远不相交，这里的表述其实是说，在平面内，两条（不重合的）直线只有两种位置关系，其中一种是相交，即两条直线仅有一个公共点，还有一种是平行，即两条直线没有任何交点.两条直线会不会有两个或者两个以上的公共点呢？如果有，两条直线一定重合！（两点确定唯一的一条直线）

对于两条直线之间的平行关系，其实有多种理解方式：

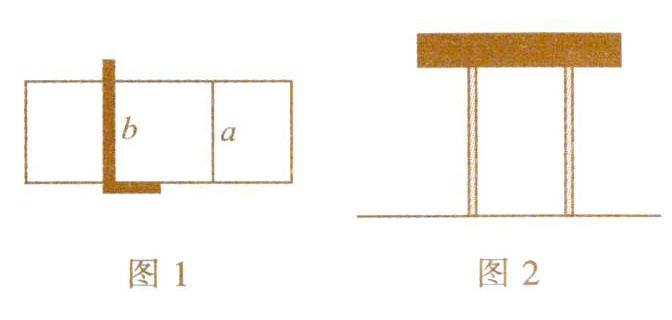
（1）木工师傅虽然不一定学过数学，却能画平行线，方法是通过“两条垂直于同一直线的直线互相平行”的操作活动，如图1所示，

其中的道理就在于，在同一平面内，只要两条直线同时垂直于同一条直线，这样的两条直线就是相互平行的.

（2）两条直线总是有相同的距离，这两条直线是平行的，例如，图2中的两根柱子都是直立的，其长度是一样的，这时，横着的木条平行于地面上对应的直线.

三、在解决问题的活动中积累几何活动经验

例1如下页图3所示，要在长方形木板上截一个平行四边形，使它的一组对边在长方形的边缘上，另一组对边中的一条为AB.只有一个圆规和一把没有刻度的直尺.你能解决问题吗？

分析：同位角相等，两直线平行.过直线外一点C作已知直线的平行线，相当于过点C作∠ECD等于已知的∠CAB.

解：以点A为圆心，以任意长为半径画弧，交AB于点日，交AC于点G;再以点C为圆心，以同样长（AH）为半径画弧，交CE于点P：再以点P为圆心，以线段GH的长为半径画弧，交前面所画的弧于点D;连接CD并延长交长方形的边于点F.这样得到线段CF平行于AB于是，我们就得到了符合题意的平行四边形ABFC（如图4）.

进一步的讨论：

过直线外一点，还能有哪些方法可以画出与这條直线相互平行的直线呢？

敏敏同学认为：利用判定方法1“两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行”，需要没有刻度的直尺和三角尺.首先把三角尺的斜边放在直线a上，将直尺的一边靠在三角尺的一条直角边上;然后按住直尺不动，将三角尺紧靠直尺移动，使得三角尺的斜边过已知点;最后沿着三角尺的斜边画一条直线b，则b∥a.如图5所示，

亮亮同学认为：利用判定方法2“如果内错角相等，那么两直线平行”，需要圆规和没有刻度的直尺.首先过点P画任意一条直线b与直线a交于点A;其次以点A为圆心，以任意长为半径画弧，交直线6于点日，交直线a于点G;再以点P为圆心，以相同长度（AH）为半径画弧，交直线b于点C;然后以点C为圆心，以线段GH的长为半径画弧，交前面所画弧于点D;最后连接PD并延长得到与直线口平行的直线c.如图6所示，

小小同学认为：利用“平行线之间距离处处相等”，需要三角尺和圆规.首先，将三角尺的一条短直角边放在直线口上，移动三角尺的另一长直角边，使其过点P，沿着三角尺的长直角边画直线与直线a交于点A;然后继续移动三角尺，使其过直线a上任意点B，再次沿着长直角边画直线a的垂线;再以点B为圆心，以线段PA的长为半径画弧，与垂线交于点C;最后连接点P，C并延长得到直线b，它是与直线a互相平行的直线，如图7所示，

乐乐同学认为：只要一张纸就能找到这条平行线.先折出直线a的过点P的垂线m.再折出垂直于直线m的另一条直线b即可，两个交点处的角都是直角，由“同位角相等，两直线平行”，可得直线b是与直线a相互平行的直线.如图8所示.

对于上面四位同学的不同思路，你认为谁的思路更好呢？

四、探究图形性质，培养几何直观

1.（与同学一起合作完成）将两把直尺交叉放在一起（如下页图9），一位同学按住交叉处，另一位同学转动其中一把直尺，观察随着直尺的转动，两把直尺的夹角之间的关系.

可以发现，相邻的角相加等于1800.相对的两个角，一个角随着另一个角的增大（减小）而增大（减小），对顶角相等.

2.一位同学在白纸上，固定三角尺ABC的AC边，并延长AC.另一位同学将三角尺CDE的直角顶点与三角尺ABC的直角顶点重合，并延长DC，如图10. ∠DCP与∠ACF就是一组对顶角.你能说出其中的原理吗？

请同学们自己思考.

五、发展空间观念，培养推理能力

例2如图11所示，要把角钢弯成120°的钢架，则在角钢上截去的缺口是____°.

分析：这道题主要考查了同学们的空间想象能力，

解：因为把角钢弯成120°的钢架，在截之前的角是平角180°，所以缺口的角等于180°-120°=60°.故答案为60.

例3 （2019年甘肃）如图12，将一块含有30°角的三角尺的顶点放在直尺的一边上，若∠1=48°，则∠2的度数为（  ）.

A.48°

B.78°

C.92°

D.102°

分析：如图13所示，直接利用已知角的度数结合平行线的性质得出答案.此题主要考查了平行线的性质，正确得出∠3的度数是解题关键.

解：如图13所示，将一块含有30°角的三角尺的顶点放在直尺的一边上，∠1=48°，∠ 2=∠3=180°-48°-30°=102°，故应选D.

1.（2019年济宁）如图14，直线。，6被直线c，d所截，若∠1=∠2，∠3=125°，则∠4的度数是（  ）.

A.65°

B.60°

C.55°

D.75°

2.（2019年衡阳）如图15，已知AB∥CD，AF交CD于点E，且BE⊥AF，∠BED=40°，则∠A的度数是（  ）.

A.40°

B.50°

C.80°

D.90°

3.如图16，若直线a//b，∠1=45°，∠2=30°.则∠FPE=____

_____________________.

参考答案：1.C 2.B 3.75。