隐式重启动Arnoldi迭代法在双液层流动稳定性的应用
莫东鸣,徐 敏
(重庆工业职业技术学院 机械工程学院,重庆 401120)
隐式重启动Arnoldi迭代法在双液层流动稳定性的应用
莫东鸣,徐 敏
(重庆工业职业技术学院 机械工程学院,重庆 401120)
通过引入微小扰动量,建立了描述两不相溶混的上部为固壁的环形腔内双层流体的热毛细对流的线性扰动方程。针对此复广义特征值问题,采用隐式重启动Arnoldi迭代法,在单液层流动稳定性计算中,对程序的正确性进行了验证, 结果证明该方法可应用于流体流动线性稳定性分析及节能计算。
隐式重启动Arnoldi迭代法;双液层;稳定性
0 引 言
流体动力系统的稳定性,是一个古老而现在仍非常活跃的研究领域,稳定性分析涉及到基本定态解何时被破坏,如何被破坏,以及后续的发展等。稳定性分析在工程、气象、海洋、大气物理、地球物理学中都有许多应用[1]。不少工程技术如节能技术问题已经得益于这方面的研究成果。
我们可以通过某种方法,比如相似性原理、渐近线方法求得微分方程的解,但这个解所代表的流场、温度场能否在实际中实现,在对其做稳定性分析之前是无法回答的。如果所得的解在所考虑的参数空间上是不稳定的,那么这个解实际上根本无法实现,因为所求得的解只代表了一种未受扰动情况下的流场、温度场。而工程实际中不可避免地会出现各种形式的扰动,如果系统能使各种扰动随时间衰减下去,至少不增大,即系统是渐进稳定的或稳定的,那么系统所特有的流场、温度场才可能保持下去;否则,系统所特有的状态——基本定态解,将随时间变化,从一种运动形式变为另一种运动形式,比如从定常运动变为时相关运动,因而所求得的微分方程基本定态解将毫无工程意义。
在晶体材料生长过程中,最常使用的制备方法为提拉法,为了抑制熔体的蒸发和超过临界温度之后出现热流体波对晶体质量的破坏,可以在熔体上方施加一层不相溶混的液体,此种生长晶体的方法称为液封提拉法。由于增加了液封层,使得熔体流动稳定性的研究变得复杂。在文章[2],我们已求得了具有液封环形液池内热对流的基态解,如果对求得的这个解的稳定性分析的结果能够表明在很大的控制参数(Marangoni数) 范围内解是稳定的,那么说明,这个解在很大程度上能够保持下去,即这种被削弱了的运动形式能够维持下去,那就说明通过液封削弱热毛细对流的方法在理论上是可行的;反之,如果稳定性分析的结果是:无论多小的控制参数,解都是不稳定的。由此可见,对所关心的热物理系统的基本定态解做稳定性分析,显得非常必要和特别重要。在晶体生长过程中,大量理论分析和实验研究都重视熔区对流的稳定性对生长晶体的质量将带来直接的影响。遗憾的是对具有液封的环形双液层的热毛细对流的稳定性分析还未见文献报导。本文对之做稳定性分析无疑可以弥补这方面理论的不足,同时可望对工程实际有直接的指导意义,为有关参数的选择提供重要依据。
求解稳定性方程最后可以化为求解一个特征值问题,在实际工程中所求特征值通常有些特殊的性质,例如,为了稳定性分析要求k个实部最大的特征值,或在复平面上靠近某个点的特征值。通常,随着子空间维数m的增大,Ritz对会逼近特征对。但实际计算中,m可能要非常大时,Ritz对才满足精度要求,可以通过重启动来解决这一问题。当在一个子空间中用投影类方法求解矩阵的特征值问题时,若该子空间中含有所求特征向量的信息越丰富,则收敛速度越快,这就是选择“重新启动”方式的原则之一。当期望对特征向量有更多的了解时,就用特征向量的线性组合更新启动向量,重新启动Arnoldi分解。基本思路是当Krylov子空间维数达到一设定值时,如果Ritz对仍不收敛,就重新构造“启动矢量”。用新的矢量来重新计算Arnoldi分解[1]。
由 1992年Soresen提出的隐式重启动方法,被公认为是最有效的重开始技术之一。它是一种基于隐式QR位移分解的简便和稳定的方法,不用显示计算Arnoldi分解。IRAM算法的优势在于:把一个大型的稀疏矩阵(带状矩阵,阶数为n)正交投影为一个远小于其矩阵阶数的小上Hessenberg矩阵(阶数为k),这一过程体现了空间节省的优点;通过求此小矩阵的特征值与特征向量,再经过重启动迭代技术,收敛得到近似于原矩阵的特定特征值,这一过程体现了空间节省、提高收敛精度、缩短收敛时间的优点[3]。
目前,IRAM因其合适求解大型矩阵特征值问题,且有精度高、计算时间短的优点,在相近领域如电力的动力系统稳定性分析、核科学中子输运特性等研究中得以应用,但在晶体材料生产过程中的流动稳定性分析研究中还未见报道。
1 物理模型及求解方法
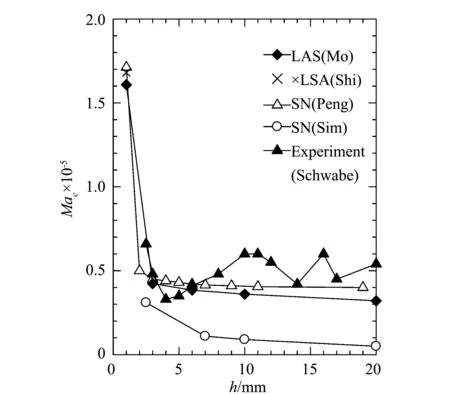
环形腔中盛载两不相容混的熔体5cSt silicone oil 与 HT-70,物性参数同文献[4]。双层液体施以水平温度梯度,上固壁温度Tc,下固壁温度Th(Tc 在模型中引入如下假设:(1)熔体和液封均为不可压缩的牛顿流体,满足Boussinesq近似;(2)流速较低,流动为轴对称二维层流;(3)两相界面平整无变形,在液液界面和自由表面均考虑热毛细力的作用,固-液界面满足无滑移条件;(4)液池顶部和底部边界均绝热;(5)表面张力是温度的线性函数。 图1 物理模型 对控制方程进行无量纲化,时间、长度、速度、温度和压力无量纲尺寸如下: (ro-ri)2/v1,ro-ri,v1/(ro-ri),ρ1v2/(ro-ri)2,则无量纲方程可写为: ▽·Vi=0, (1) (2) (3) 式中:ρi,ai,βi和vi分别为i(i=1, 2)层液体的密度,热导率,热扩散系数和动力粘度;Vi代表无量纲速度矢量;Θi(Ti-Tc)/(Th-Tc)为无因次温度;Pi为无量纲压力;τ为无量纲时间;ez为垂直方向的速度矢量;Pr=v1/a1为熔体的普朗特数。 在Z=H1=h1/(ro-ri)的液液界面边界条件为: (4) 式中:R与Z为无量纲坐标;Ma是Marangoni数,其定义式为Ma=γ2-1(Th-Tc)(ro-ri)/(μ1a1);μ为动力粘度;κ为导热率;γT=-∂γ/∂T是界面张力梯度。 径向与纵向速度用无量纲流函数ψ定义如下: (5) (6) 把方程(6) 代入方程 (1-4) 并消去非线性项,则获得线性扰动方程。于是,方程可化简为一个广义特征值问题: (7) 式中:A、B为具有复元素的复矩阵;n为节点数;x为特征向量,包含所取节点上的未知速度、温度和压力值的特征向量。求解方程(7)的特征值,当特征值λ为零时,可得到临界 Marangoni数Mac。至此,将稳定性分析问题转化成为一个复广义特征值问题。 稳定性分析的根本任务是要在参数Pr,m,μ,α,γT等取定后,确定特征值第一次跨过虚轴所对应的Marangoni数,通过一连续增加Ma的过程,实现临界Marangoni数的确定。即在μ*,κ*,ρ*,ν*,α*,Pr等取定后,取一足够小的Ma0作为初值,令Ma=Ma0。计算系统实部最大特征值λmax,视其实部Real(λmax) 是否大于0,并增加Ma重新计算;如此记录特征值,在最大特征值为零的交界处便可以得到临界Marangoni数。 显然,我们并不计算全部特征值,而是计算所关心的主导特征值。由于上述矩阵为带状矩阵,所以选用IRAM法。ARPACK软件包是基于隐式重启动Arnoldi方法的Fortran77子程序的集合。该软件使用n·O(k)+O(k2)的存储开销计算满足用户要求的k个特征值,这包括具有最大实部、最大虚部或最大模的特征值。因为低存储和计算需求,这个技术适合大规模特征问题[5-6]。 为了检验程序的正确性和网格的收敛性,在环形单液层与环形双液层系统分别做了相关验证。在环形单液层系统中,在与文献[7-8]相同的条件及计算网格下进行了线性稳定性计算,计算结果与文献的结果非常接近,说明程序是正确的。具体结果分析如下。 对于ro=40 mm和ri=40 mm,在微重力情况下的环形浅液池进行了线性稳定性分析,物性值取与文献[8]完全相同。Shi等人在二维数值模拟中,取网格(122-542)R×(16-28)Z,在三维数值模拟中,取网格(82-202)R×(123-603)θ×16Z,故在线性稳定性分析计算中取网格300R×60Z。图2为文中线性稳定性分析临界Marangoni数结果与三维数值模拟、实验、其它线性稳定性分析结果的对比。以1 mm厚度为例,Shi等人的三维数值模拟的Mac=1.68×105,mc=27,Emakov等人的线性稳定性分析Mac=1.68×105,mc=28,本文线性稳定性分析计算Mac=1.608×105,mc=28, 相对误差为4.29%,计算结果与他们的数值模拟与理论结果非常接近,说明程序是正确的。 图2 单液层微重力情况下发生热流体波的临界Marangoni数 图3给出了1 mm厚度下,Mac=1.61×105,线性稳定性分析确定的自由表面热流体波形态比较结果,此时热流体波运动方向与温度梯度方向间夹角约为58°,如图3(a)所示。Shi等人的线性稳定性分析结果和三维数值模拟结果分别如图3(b)和(c)所示,可以看出波数相同,传播角相近,从而说明程序在计算特征向量时也是可靠的。 图3 首先通过引入微小扰动量,建立了描述两不相溶混的上部为固壁的环形腔与有自由表面的环形池内双层流体的热毛细对流的线性扰动方程。在此基础上,用有限差分方法离散线性扰动方程,经离散化处理,得到了离散化方程组及边界条件,该方程组构成了一个复广义特征值问题;针对问题的特点采用隐式重启动Arnoldi迭代法,以保持矩阵的带型结构,通过编程计算求解;在单液层系统中对程序的正确性及网格的独立性都进行了验证,程序证明利用IRAM解决环形池内流体系统稳定性具有适合大型带状矩阵特征值问题、计算快速、可求解多重特征值的优点。后续可在单液层稳定性分析的基础上进行双液层流动稳定性问题的计算。 [1] P.G.德拉津,W.H.雷德,周祖巍,等.流体动力稳定性[M].宇航出版社,1990. [2] Li Y R, Zhang W J, Peng L. Thermal convection in an annular two-layer system under combined action of buoyancy and thermocapillary forces [J]. J. Supercond. Nov. Magn., 2010, 23: 1219-1223. [3] G.W.斯图尔特. 矩阵计算引论[M].上海科学技术出版社,1980. [4] 曹志浩. 矩阵特征值问题[M]. 上海科学技术出版社,1980. [5] Lehoucq RB. Implicitly Restarted Arnoldi Methods and Subspace Iteration[J]. SIAM Journal on Matrix Analysis and Applications, 2001,23(2):551-562. [6] Lehoucq RB. Sorensen D C, Vu etal P A. ARPACK:Fortran subroutines for solving large scale engenvalue problems[R]. Release 2.1. [7] Peng L, Li Y R, Shi W Y, .Three-dimensional thermocapillary-buoyancy flow of silicone oil in a differentially heated annular pool [J]. Int.J.Heat Mass Transfer, 2007, 50(5-6):872-880. [8] Shi W Y, Ermakov M K, Imaishi N.Effect of pool rotation on thermocapillary convection in shallow annular pool of silicone oil[J]. J.Crystal Growth, 2006(294):474-485. [9] 石万元,李友荣,M.K.Ermakov,今石宣之.环形液层内热毛细对流的线性稳定性分析[J].工程热物理学报,2008,29(7): 1218-1220. Application of Implicit Restarted Arnoldi Method on Flow Stability of Two-layer Liquid System MO Dong-ming,XU Min (Department of Mechanical Engineering, Chongqing Industry Polytechnic College, Chongqing 401120, China) By introducing a small disturbance quantity, the linear perturbation equation described thermocapillary flow in a two-layer system with upper rigid wall was set up. For the generalized eigenvalue problem, the Arnoldi restart implicit iteration method was adopted. This method was verified in a single layer system in the correctness of the program, the results proved that it can be applied to linear stability analysis and energy saving calculation. Implicit restarted; Arnoldi method;Two-layer; Lquid system; Flow stability 10.3969/j.issn.1009-3230.2015.03.003 2014-02-10 2015-02-27 重庆市教委科学技术研究项目(自然科学类)(KJ132104);第二批重庆市高等学校青年骨干教师资助计划(自然科学类);重庆工业职业技术学院科研项目(GZY201313) 莫东鸣(1982-),女,广西南宁人,博士,讲师,重庆大学动力工程与工程热物理专业,从事晶体材料制备中热物理问题的研究。 TP137.7 B 1009-3230(2015)03-0013-05
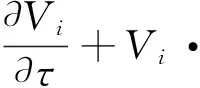


2 程序正确性验证

3 结束语

