T型模具变歧管半径流道的流变学设计

麻向军

(华南理工大学 聚合物成型加工工程教育部重点实验室∥聚合物新型成型装备国家工程研究中心，广东 广州 510640)

热塑性塑料片材、流涎膜挤出成型采用平缝型挤出模具，其流道设计的关键问题包括熔体沿流道宽度方向出口流率要均匀一致、熔体流经整个流道的压力降要适中以及熔体在流道中的停留时间尽可能短[1- 2]。T型挤出模具结构简单、制造成本低，特别是流道宽度较大时，T型模具的流道长度较衣架式模具小，更适合于宽幅片材和流涎膜挤出成型。现有T型模具的流道设计只能以等歧管半径和等厚度阻流区流道的熔体出口流率均匀性指数UI作为设计校核依据[1]，如式(1)所示：

(1)

式中，n为熔体的幂律指数，h为阻流区厚度，L为阻流区长度，R为歧管半径，W为流道宽度的一半。

从式(1)可以看出，UI<1，工程中通常以UI≥0.95作为设计依据。受模具长度的限制，通常采用增加歧管半径和减小阻流区厚度的方法提高熔体出口流率的均匀性。但是，增加歧管半径会显著增加熔体(特别是靠近流道末端的熔体)的停留时间，容易造成熔体的热降解；减小阻流区厚度会显著增加挤出压力，增大挤出难度，降低挤出产量。工程上亦采用将阻流区设计为厚度不同的两个区域的方式来降低熔体停留时间和挤出压力[3]，但由于缺乏设计理论的指导，通常需要加装阻流棒或/和采用柔性模唇并在试模时通过局部调节来提高熔体出口流率的均匀性[4- 5]，这不仅使模具结构变得复杂，而且增加了模具制造成本。设计不良的流道即使调节阻流棒和柔性模唇也难以使熔体出口流率的均匀性达到理想状态，而且容易造成熔体滞留[6- 7]。麻向军[8]采用等歧管半径和两个不同厚度阻流区的流道结构，基于熔体出口流率均匀的条件推导了阻流区分界曲线的解析式。本研究在分析T型模具中熔体在流道中的流动特点的基础上，提出了采用变歧管半径和两个不同厚度阻流区的流道结构，并在满足熔体出口流率沿流道宽度方向均匀的条件下，根据流变学理论对流道结构和尺寸进行理论设计，最后进行了设计实例研究。

1 流道几何形状的流变学设计

1.1 几何模型

采用变歧管半径和两个阻流区的流道结构如图1所示，由入口区、歧管、阻流Ⅰ区、阻流Ⅱ区、松弛区和成型区组成。熔体进入歧管后，沿歧管向流道两侧流动的同时，一部分熔体进入阻流Ⅰ区并沿挤出方向流动，因此，歧管中熔体的体积流率逐渐减小。如采用等半径的歧管，歧管中熔体的流速下降较快，停留时间迅速增加。为此，将歧管截面尺寸沿流道两侧逐渐减小以提高熔体的流速，从而降低歧管中熔体的停留时间。另一方面，熔体沿歧管向流道两侧流动时压力逐渐下降，即熔体在阻流Ⅰ区入口处的压力逐渐下降，特别是采用变半径的歧管时熔体压力下降更大，如采用等厚度阻流区，则熔体出口流率沿流道两侧降低，为了提高熔体出口流率的均匀性，必须提高熔体流经阻流区的压力降，这会造成挤出压力显著增加。为此，将阻流区设计为厚度不同的两个区域，通过改变两个阻流区的相对长度沿流道两侧的变化，使熔体流经阻流区的压力降沿流道两侧降低，以提高熔体出口流率的均匀性。图1为阻流Ⅰ区厚度较大、阻流Ⅱ区厚度较小的流道结构示意图，阻流Ⅰ区在流道对称面位置与歧管之间、阻流Ⅱ区在流道末端与松弛区之间留有适当间距以方便模具制造。在满足出口流率沿流道两侧均匀的条件下，可通过对歧管尺寸和阻流区厚度的设计，进而对两个阻流区的分界曲线进行设计。

图1 变歧管半径的T型挤出模具流道示意图

1.2 阻流Ⅰ区和阻流Ⅱ区分界曲线的理论推导

考虑到流道在宽度方向的对称性，取流道的一半进行分析，如图2所示。图中r为x处的歧管半径;h1和h2分别为阻流Ⅰ区和阻流Ⅱ区的厚度;LD为阻流区的总长度;yC和yE分别为阻流区分界曲线在流道对称面和流道末端处的坐标，数值上分别等于阻流Ⅰ区在流道对称面和流道末端的长度。为便于分析，忽略入口区的影响，歧管截面选取圆形。

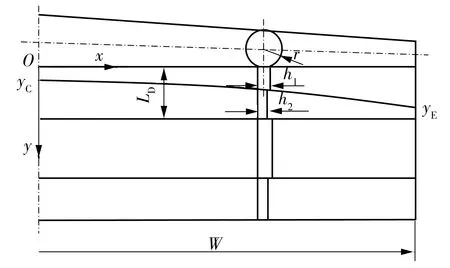
图2 变歧管半径的T型挤出模具流道设计模型

分析塑料熔体在流道中的流动时，可做如下假设[1- 2]：

(1)熔体为不可压缩流体；

(2)熔体流动为充分发展的稳态层流流动，忽略惯性力和体积力；

(3)熔体在歧管中仅沿歧管轴向流动，在阻流Ⅰ区、阻流Ⅱ区、松弛区和成型区中仅沿挤出方向流动，且熔体在歧管中的流动和在阻流Ⅰ区中的流动互不干涉；

(4)忽略歧管中由于歧管半径变化引起的拉伸对熔体流动的影响及流道两侧壁面对熔体流动的影响；

(5)熔体在流动过程中温度不变，熔体黏度对剪切速率的依赖关系采用幂律模型，即

(2)

在以上假设条件下，熔体沿歧管流动时的压力梯度可表示为[9]

(3)

式中：p为歧管中熔体在x处的压力；Q为歧管中熔体在x处的体积流率。

假定熔体在流道入口处的体积流率为2Q0，熔体出口流率沿流道宽度方向均匀时，有

Q=Q0(1-x/W)

(4)

式(4)代入式(3)，有

(5)

在任一位置x处，熔体在阻流Ⅰ区和阻流Ⅱ区中沿挤出方向流动时的压力降可表示为[8]

(6)

式中,ΔpD为阻流区中的压力降，y为阻流Ⅰ区和阻流Ⅱ区分界曲线的坐标。

松弛区和成型区的厚度和长度沿流道宽度方向不变，要求熔体出口流率沿流道宽度方向均匀，则熔体在阻流Ⅱ区出口处的压力沿流道宽度方向不变，即熔体在歧管中沿流动方向的压力梯度与熔体在阻流区中的压力降沿流道宽度方向的梯度相等，有

(7)

由式(5)-(7)可得

(8)

式(8)即为阻流Ⅰ区和阻流Ⅱ区的分界曲线在图2所示坐标系中的微分方程。

1.3 讨论

(1)由式(8)可以看出，阻流Ⅰ区和阻流Ⅱ区的分界曲线与歧管半径沿流道宽度方向的变化、阻流Ⅰ区和阻流Ⅱ区的厚度、流道宽度以及熔体的幂律指数有关，与熔体的稠度和产量无关。流道宽度由产品规格确定，幂律指数是熔体的材料参数，而歧管半径、阻流Ⅰ区和阻流Ⅱ区的厚度均可作为流道的设计参数，根据式(8)对阻流Ⅰ区和阻流Ⅱ区的分界曲线进行设计。

(2)阻流Ⅰ区和阻流Ⅱ区的厚度沿流道宽度方向不变，而歧管半径沿流道宽度方向减小且其末端尺寸不为0时，式(8)难以得到解析式，需要采用数值方法求解并拟合得到阻流Ⅰ区和阻流Ⅱ区的分界曲线。其边界条件为

y|x=W=yE

(9)

yE根据加工条件确定。由式(8)可以看出，y是x的单调增函数；当h1>h2时，阻流Ⅰ区的长度沿流道宽度方向增加；当h1

当歧管半径沿流道宽度方向不变时，可对式(8)直接积分，利用式(9)得到阻流区分界曲线的解析式，与文献[8]中的阻流区分界曲线表达式相同。

(3)熔体由歧管入口沿任一路径流经歧管和阻流区到达阻流Ⅱ区出口处的压力降相等，可用流道对称面处的压力降计算，即

(10)

(4)歧管中的熔体由入口到达任一位置x处的停留时间t可表示为

(11)

当歧管半径沿流道宽度方向减小且末端尺寸不为0时，式(11)需要采用数值方法求解，其边界条件为

t|x=0=0

(12)

2 流道设计实例

2.1 分界曲线的验证

以HDPE片材挤出为例，采用ANSYS Polyflow软件对熔体在流道中的流动进行数值模拟，通过熔体出口无量纲流率(即沿流道宽度方向某一位置单位宽度的体积流率与平均单位宽度的体积流率的比值)对变歧管半径时阻流Ⅰ区和阻流Ⅱ区的分界曲线方程的可靠性进行验证。

采用幂律模型描述HDPE的流变性能，挤出温度为170 ℃时，K=7 083 Pa·s-0.504，n=0.496[10]。片材宽度取2 000 mm，松弛区的长度和厚度分别取45 mm和4 mm，成型区长度和厚度分别取25 mm和1.5 mm，挤出速度取20 mm/s。假定歧管半径线性减小，在流道对称面和末端处的半径分别取15 mm和6 mm，阻流Ⅰ区和阻流Ⅱ区的厚度分别取2 mm和0.9 mm，总长度取40 mm，阻流Ⅰ区在流道末端的长度取34 mm，采用四阶显式Runge-Kutta法[11]求解分界曲线的微分方程，计算得到阻流Ⅰ区在流道对称面处的长度为6.3 mm。

采用样条曲线拟合分界曲线并对流道进行建模，取其宽度方向的一半进行计算。为提高计算精度，采用六面体单元划分流道，流道壁面边界和尺寸突变位置采用较小尺寸的网格，流场求解时速度采用二次插值，压力采用线性插值。

模拟计算得到的熔体压力等值线和出口无量纲流率沿流道宽度的变化如图3所示。由图3可以看出，当熔体离开阻流区时，熔体的压力沿流道宽度方向不变，流道对称面处熔体在阻流区的压力降与理论计算一致。在流道对称面处熔体出口无量纲流率为0.995，沿流道宽度方向熔体出口无量纲流率逐渐增加，距离流道末端约20 mm处熔体出口无量纲流率达到最大值1.016；之后开始下降，仅在流道末端约5 mm的范围内，熔体无量纲出口流率小于1。这是由于理论推导中忽略了流道侧壁对熔体流动的影响，而模拟计算时熔体与侧壁之间为无滑移边界，与实际生产一致。

图3 数值模拟结果

2.2 设计实例

针对2.1节中的片材规格、挤出速度和材料，在保持阻流区长度不变的情况下，采用不同变化规律的歧管半径，利用式(8)对阻流区厚度和分界曲线进行设计，并对流道对称面处熔体在阻流区的压力降和熔体在歧管中的停留时间进行比较。熔体在歧管中的停留时间沿流道宽度方向增加，靠近流道两侧，熔体在歧管中的停留时间远大于熔体离开歧管后的停留时间，为便于比较，选择歧管中距离入口0.95W处的熔体停留时间进行比较。熔体由歧管入口沿任一路径流经歧管和阻流区到达阻流Ⅱ区出口处的压力降沿流道宽度方向不变，且对挤出压力有重要影响，为便于比较，选择流道对称面处熔体在阻流区的压力降进行比较。

采用传统设计方法(即阻流区长度、阻流区厚度及歧管半径均沿流道宽度方向不变)，当阻流区厚度分别为0.9 mm和0.7 mm时，根据式(1)，要使UI≥0.95，歧管半径R必须大于37 mm和30 mm，流道对称面处熔体在阻流区的压力降分别为10.62 MPa和17.51 MPa，歧管中距离入口0.95W处的熔体停留时间分别为429.5 s和282.4 s。由于阻流区的厚度和长度沿流道宽度方向不变，而阻流区入口处的熔体压力沿流道宽度方向减小，因此，要提高熔体出口流率的均匀性，必须使熔体流经歧管的压力降远小于熔体流经阻流区的压力降，减小歧管半径时，必须增大熔体流经阻流区的压力降，造成挤出压力增大，而增加阻流区厚度时，必须增加歧管半径，造成熔体停留时间增加。

采用两个不同厚度的阻流区，当歧管半径沿流道宽度方向不变时，式(8)和式(11)均可得到解析解。仍以上述片材为例，取歧管半径为15 mm，阻流Ⅰ区和阻流Ⅱ区的厚度分别取1.8 mm和1.2 mm，阻流Ⅰ区在流道末端的长度取34 mm，计算得到阻流Ⅰ区在流道对称面处的长度为5.6 mm，流道对称面处熔体在阻流区的压力降为5.52 MPa，歧管中距离入口0.95W处的熔体停留时间为70.6 s。与采用传统设计方法得到的歧管半径为37 mm和 30 mm的流道相比，对称面处熔体流经阻流区的压力降分别下降了48.0%和68.5%，而歧管中距离入口0.95W处的熔体停留时间分别下降了83.6%和75.0%。可以看出，采用两个不同厚度的阻流区时，无论是熔体停留时间还是流道对称面处熔体流经阻流区的压力降都显著下降。

为了进一步降低熔体在歧管中的停留时间，选择歧管半径沿流道宽度方向按幂律减小，即

r=RC-(RC-RE)(x/W)m

(13)

式中，m为歧管半径沿流道宽度方向变化的指数，RC为流道对称面处的歧管半径，RE为流道末端的歧管半径。

取RC=15 mm、RE=6 mm、yE=34 mm,兼顾流道的可制造性，选择两个阻流区的厚度，采用四阶显式Runge-Kutta法求解式(8)可得到阻流Ⅰ区和阻流Ⅱ区的分界曲线坐标，根据式(10)计算对称面处熔体在阻流区的压力降，采用四阶显式Runge-Kutta法求解式(11)可得到歧管中距离入口0.95W处的熔体停留时间，如表1所示。

表1 歧管半径变化规律对熔体停留时间和压力降的影响

从表1可以看出，随着m的增大，熔体的停留时间增加，而流道对称面处熔体在阻流区的压力降减小。由式(13)可知，0≤x/W≤1，流道宽度方向距对称面的距离一定(即固定x)时，歧管半径随着m的增大而增加，而歧管中熔体的体积流率相同，因此，熔体的流速和压力梯度均随m的增大而减小，歧管中熔体停留时间随m的增大而增加，流道对称面处熔体流经阻流区的压力降随m的增大而减小。

与歧管半径不变的流道相比，歧管半径沿流道宽度方向减小时，距离对称面相同位置，歧管中熔体的流速和压力梯度增大，故熔体的停留时间减小，而对称面处熔体流经阻流区的压力降增加。与采用传统方法设计的歧管半径为30 mm的流道相比，当m分别为1、2和3时，对称面处熔体流经阻流区的压力降分别下降了47.1%、56.3%和63.7%，而歧管中距离入口0.95W处的熔体停留时间分别下降了90.7%、87.6和85.6%。由此可以看出，传统的流道设计方法在提高熔体出口流率均匀性时，会引起挤出压力显著增加或熔体停留时间显著增加，而文中提出的流道设计方法可以在较低的挤出压力下，显著降低熔体的停留时间。

3 结论

本研究首先针对T型模具变歧管半径的流道，将阻流区设计为两个厚度不同的区域，基于熔体出口流率均匀的条件，推导了阻流Ⅰ区和阻流Ⅱ区分界曲线的微分方程，对该方程进行数值求解，以用于流道歧管半径、阻流Ⅰ区和阻流Ⅱ区的厚度及其分界曲线的设计。然后采用四阶显式Runge-Kutta法求解阻流Ⅰ区和阻流Ⅱ区分界曲线的微分方程并建立流道几何模型，通过数值模拟对设计的流道进行了验证，结果表明所推导的分界曲线微分方程是可靠的，能够指导T型挤出模具的流道设计。最后通过设计实例，与歧管半径和阻流区厚度不变的流道进行了对比研究，结果表明采用变歧管半径和两个不同厚度阻流区的流道在满足熔体出口流率沿流道宽度方向均匀的条件下，既可以显著降低模具的挤出压力，又能够显著降低熔体在流道中的停留时间。