基于LabVIEW的TDLAS检测系统多参数影响研究

叶玮琳 涂子涵 肖旭鹏 周波 潘易宇 郑志丹 吴涛 吴福培 徐严平 郑传涛

(1.汕头大学 智能制造技术教育部重点实验室∥工学院，广东 汕头 515063;2.汕头大学 分析测试中心，广东 汕头 515063;3.吉林大学 电子科学与工程学院∥集成光电子学国家重点联合实验室吉林大学实验区,吉林 长春 130012)

红外吸收光谱法因具有不受电磁干扰、无化学污染、易于采样、高灵敏度、可小型化等优点[1]，如今被广泛用于空气质量检测、在线气体分析、医学诊断和农业工业排放物监测等领域[2]。可调谐二极管激光吸收光谱(TDLAS)作为红外检测技术中的一种，更适合于对分辨率、灵敏度和准确性要求较高的场合[3- 4]。

然而，在实际应用中表征气体体积分数的二次谐波信号的特征会受不同技术参数的影响。Zhang等[5]针对激光器的调制特性，研究了谐波信号与调制度、调制频率和激光器工作温度的关系，并得出了最佳调制参数。Alorifi等[6]基于LabVIEW的基础，研究了目标气体体积分数与线宽参数对吸收曲线和二次谐波曲线的影响。文献[7]基于实际CO2的TDLAS系统,研究了TDLAS系统的调制参数对谐波信号的影响，并给出了参数选择和优化方法。

完整的红外光电检测系统包含光学、硬件与软件等部分，各部分均会对最终的谐波信号以及气体体积分数检测结果产生影响[5,7]。现有的研究，多数是在实际检测系统的基础上进行研究，缺乏对多参数影响的完整讨论。文中首先研究了激光器输入电压、激光波数、探测器信号等硬件因素之间的关系；然后，通过HITRAN数据库导出吸收强度线型进行拟合[8]；最终基于实际系统将TDLAS仿真程序写入LabVIEW软件中，除去环境与硬件因素的干扰，有针对性地研究激光器的调制因素、滤波器阶数对二次谐波信号的影响。

1 理论分析

1.1 比尔朗伯定律

在红外气体检测中，红外光通过气体时，气体会根据相应吸收谱线的线型函数对光产生吸收作用，透射光与入射光强度会成一定比例关系，即比尔朗伯定律[9]

It=I0exp[-φ(ν,ν0)SPCL]

(1)

其中：It为入射光强；I0为透射光强；φ(v)为气体吸收线型函数；ν为波数，cm-1；ν0为气体吸收峰中心波数，cm-1；S为气体吸收线型强度，cm-2/Pa;P为气体环境压强，Pa；C为气体体积分数，%；L为光程长度，cm。

吸收系数用下式表示为

A(v)=ln[I0(ν)/I(ν)]=φ(ν,ν0)SPCL

(2)

以该吸收线型谱线为基础，可通过线型拟合得到气体关于波数、压强、光程长度以及气体体积分数的线型函数，从而进一步模拟吸收信号。

1.2 谐波检测理论

在TDLAS系统，为实现可调谐激光光谱，需要调制激光器的输入电流，其输出的激光的光强为Ic(t)+ΔIcos(ωt-Δφ)。其中：Ic(t)为激光器输出中心波数对应的光强，ΔI为光强调制波数对应的光强，ω为调制角频率，Δφ为激光器输出光强与光波数的相位差。

调制光经过待测气体吸收后，由探测器检测到的光信号为V(t)，其可表示为正弦调制光转换后得到的信号Assin(ωt+θ)与扫描光转换后得到的信号n(t)之和，其中θ为探测器电信号与锁相放大电路参考光之间的相位差。将探测到的电信号经过锁相放大电路，与幅值为Br的参考信号Vref(t)相乘，再经过低通滤波器，最终输出为直流分量1/2AsBrcosθ。

当θ=0°时低通滤波器输出谐波信号幅值最大；当θ=90°时，低通滤波器输出信号为0，此时低通滤波器输出信号Vlowpass即为一次谐波信号，要提取二次谐波，只需将2倍频的参考信号与输入信号相乘，再经过低通滤波器即可得到。

2 谐波检测仿真

2.1 吸收强度线型仿真

在LabVIEW中重构洛伦兹线型，波数范围为6 046.5～6 047.5 cm-1。6组不同温度和压强下甲烷吸收强度的数据仿真吸收线型、原HITRAN数据库中甲烷的吸收线型以及两种线型的全高与半高全宽的对比如图1所示。

选取吸收线型的全高与半高全宽进行对比，是因为这两项特征在红外吸收谱线中较常见且具有代表性。由图1(a)、1(b)可见，随着气体压强的增大，吸收线型半高全宽值逐渐增大;由图1(c)可见，随着压强的增大，仿真线型与HITRAN数据库线型的半高全宽值逐渐接近。对6组LabVIEW模拟产生的吸收强度数据与对应的HITRAN数据库导出数据进行相关性分析，结果表明，在温度300 K，压强分别为60 795、81 060、101 325、121 590、141 855、162 120 Pa条件下其相关系数分别为0.999 69、0.999 92、0.999 96、0.999 95、0.999 96、0.999 97，即重构数据与数据库真实数据重合度达到了99.9%以上。

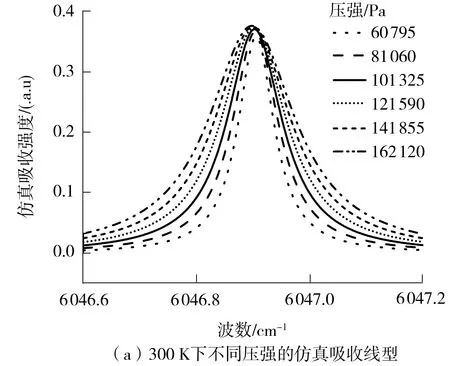
图1 LabVIEW重构线型与HITRAN数据库中相应线型对比

2.2 电流与激光波数的关系

实验使用四川超光通信有限公司生产的型号为SWLD-165310S22-01的DFB激光器，其中心波数为6 046.9 cm-1。通过傅里叶光谱仪采集激光器在不同输入电流下的输出激光的波长，线性拟合得到激光的波数与电流的关系如图2所示。可以看出电流与波数基本成线性相关，其拟合相关度为0.956 07，在后续研究中将两者关系以线性相关作为参考。

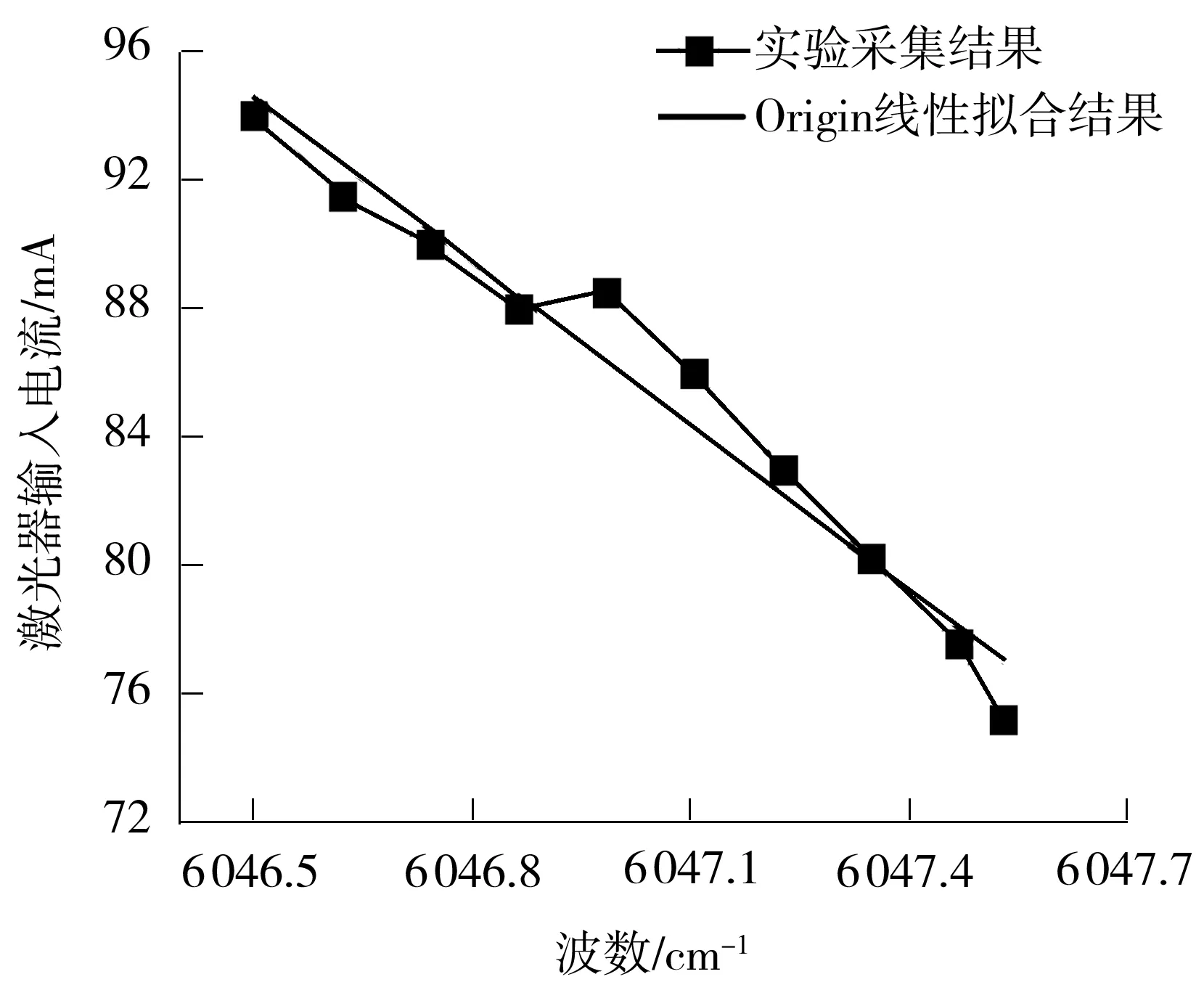
图2 激光器输入电流与波数的关系

2.3 LabVIEW吸收程序

为了满足气体吸收谐波信号的仿真需求，根据前文2.1节和2.2节的结果，使用LabVIEW程序对探测器接收到的信号进行编程仿真。该信号包括背景信号与吸收信号。背景信号基于波长调制由正弦波与锯齿波叠加产生，吸收信号由吸收强度线型仿真与比尔朗伯定律完成，程序结构框图如图3所示。

图3 LabVIEW程序结构框图

2.4 锁相放大电路提取谐波信号

TDLAS技术中，最重要一环即为通过锁相放大方法提取谐波信号。需要将与输入信号中需求信号同频的参考信号与输入信号同时导入乘法器，通过低通滤波器滤除其他信号，输出带有需求信号幅值的直流分量信号[11]，其原理如图4所示。

图4 锁相放大器原理框图

3 不同参数对谐波信号的影响

激光器调制信号及锁相放大对TDLAS检测结果起着至关重要的作用；调制信号由锯齿波与正弦波组成，这两个信号的特征参数为调制度、调制频率、扫描幅度、扫描频率；锁相放大器的性能取决于滤波器阶数。因此本研究将讨论环境因素不变的条件下调制度、调制频率、扫描幅度、扫描频率、滤波器阶数这5个参数对二次谐波信号特征的影响。

3.1 调制度对谐波信号的影响

对于TDLAS系统，二次谐波幅值与待测气体的体积分数呈正比例关系，谐波幅值越大，系统的探测下限越高，探测下限是TDLAS系统性能的首要指标，因而在调制度的调节中首先要保证的是取得谐波最大幅值；增加谐波信号的峰宽值和对称度也能够提高谐波信号的检测精度，因此同样需要考虑。保持其他参数不变的条件下，采集8个不同调制度下的二次谐波信号，所采集的二次谐波信号及其谐波幅值、对称度以及峰宽与调制度的关系如图5所示。

由图5(b)可见，二次谐波信号的谐波幅值在一定调制度下达到最大值，随后继续增大调制度会导致谐波信号幅值下降。

由图5(c)可见，对称度随着调制度的增大先升高后降低；谐波信号在一定调制度下能取得一个对称度最高的波形，但对称度总体在较小范围内波动，调制度对谐波对称度影响并不大。

由图5(d)可见，峰宽随着二次谐波调制度的增加逐渐增大。因此基于文中的测量系统，为了达到较高的测量精度，选择0.010 V的调制度。

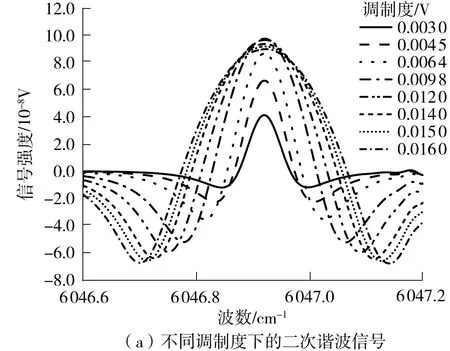
图5 调制度对谐波信号的影响

3.2 调制频率对谐波信号的影响

在调制度、扫描幅度、扫描频率不变的条件下，采集800～2 400 Hz范围内6个不同调制频率下的二次谐波信号，所采集的二次谐波信号及其谐波幅值、对称度以及峰宽与调制频率的关系如图6所示。

图6 调制频率对谐波信号的影响

由图6(b)可见，由于信号中存在1/f噪声，谐波幅值随着调制频率的增大先迅速减小再迅速增大，然后基本趋于稳定；在1 000 Hz处达到最小值，此后进一步增大调制频率，1/f噪声得到抑制，谐波幅值又迅速增大，在调制频率增大至1 400 Hz以后基本趋于稳定、呈小幅下降趋势[7]。

由图6(c)和图6(d)可知，谐波信号的对称度和峰宽随着调制频率的增加变化过程比较复杂、非单调变化。综合图6(c)和6(d)可得，理论上文中的测量系统选择2 200 Hz左右的调制频率最为合适，可以保证谐波信号幅值较大的条件下取得较高的峰宽。

3.3 扫描幅度对谐波信号的影响

在0.044～0.084 V范围内采集不同扫描幅度下的5组二次谐波信号，采集到的谐波信号如图7所示。

由图7可见，当扫描幅度小于0.054 V时，谐波信号不完整，未能覆盖气体吸收峰；当扫描幅度大于0.074 V时，二次谐波信号在较大波数范围内接近于0。扫描幅度对谐波信号的对称性以及峰宽的影响均较小，可认为图中各谐波信号重合，因此对于文中测量系统，选择0.064～0.074 V的扫描幅度，不仅能采集到完整的谐波波形，此时谐波波数中心也处于信号采集的中心点数附近，便于后续观察研究。

3.4 扫描频率对谐波信号的影响

在1～10 Hz范围内选取6个不同的扫描频率，采集二次谐波信号，所采集的二次谐波信号及谐波幅值、对称度以及峰宽与扫描频率的关系如图8所示。

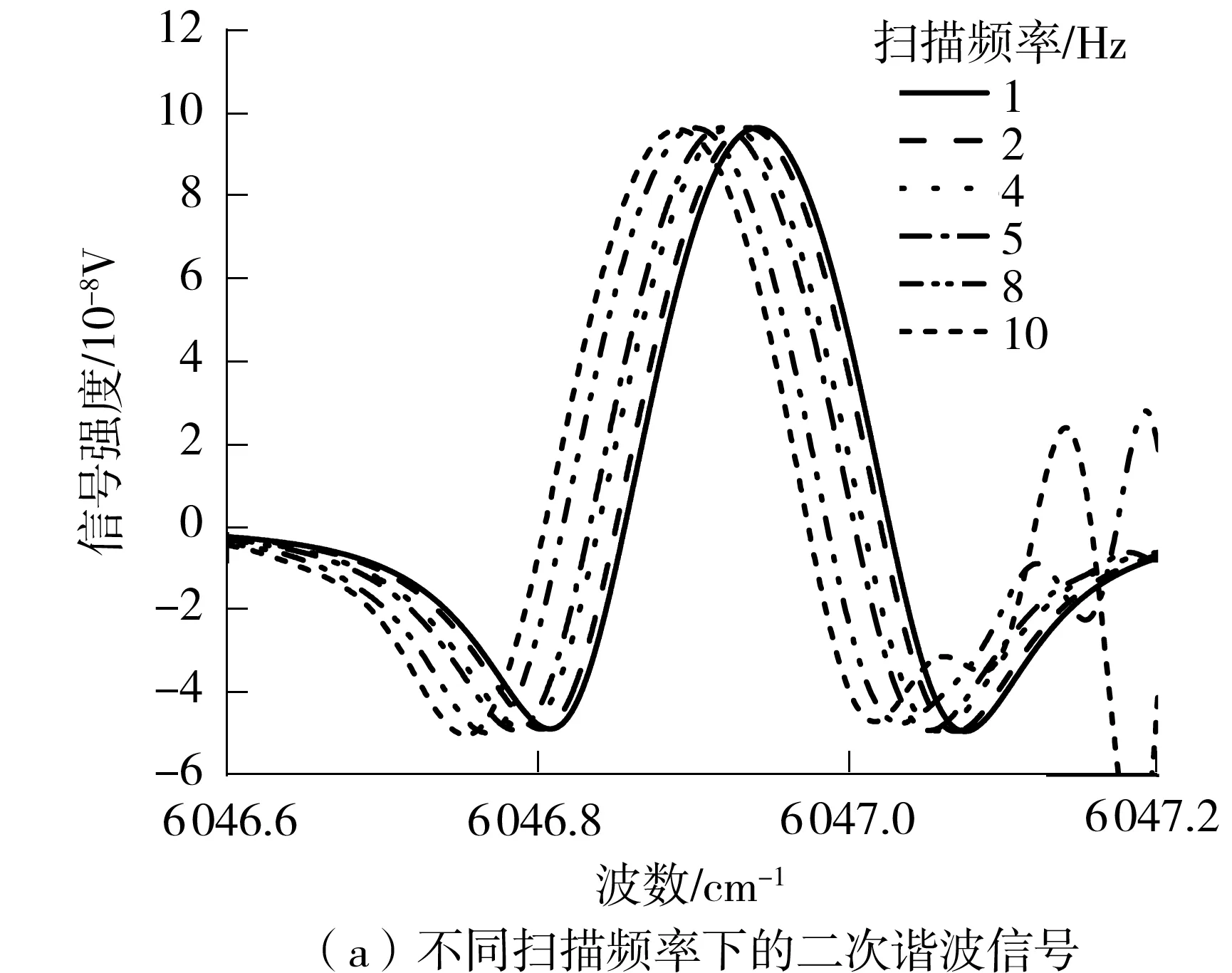
图8 扫描频率对谐波信号的影响

由图8可见，谐波信号幅值随着扫描频率的增加先基本不变，随后下降；对称度与峰宽都是先随着扫描频率的增加而增大，在增加到一个最高点后开始下降，即存在某一扫描频率能够取得最大对称度或峰宽。如果系统需反演压强，则优先选择对称度接近于1的扫描幅度。因此文中的检测系统选择5 Hz作为扫描频率，这样不仅能使得在较高的谐波幅值处有良好的对称度，还能得到较强的峰宽。过大的扫描频率会产生较低的谐波幅值、对称度以及峰宽，还会导致每个周期信号点数减少，降低检测精度并加重激光器工作负担。当扫描频率数值过高时，谐波信号会因残余幅度调制产生失真现象，谐波信号中心波数发生偏移，在检测中应避免这种情况。

3.5 滤波器阶数对谐波信号的影响

在巴特沃斯低通滤波器3-20阶数范围内取8个不同的阶数进行二次谐波采样，其他参数不变，所采集的二次谐波信号及谐波幅值、对称度、峰宽与阶数的关系如图9所示。由于3阶滤波器得到的谐波信号并未完全滤除高频信号，得到的谐波信号没有参考意义，20阶滤波信号受到残余幅度调制影响较大，难以得到峰谷值，因此除去这两组谐波信号、保留剩下的6组。

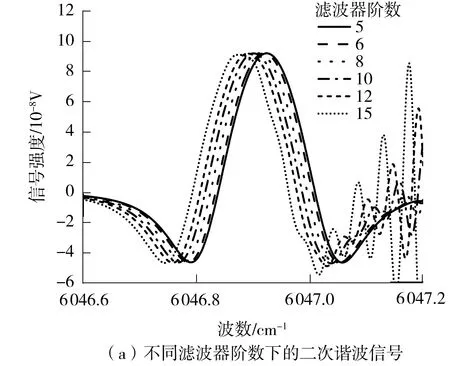
图9 滤波器阶数对谐波信号的影响

由图9可见，谐波信号幅值随阶数增加呈现单调递减的趋势；谐波对称度随滤波器阶数的增加先小幅度增大，向1逼近，随后大幅度下降；峰宽值随阶数的增加先升高后降低。理论上滤波器的阶数越高，滤波器的性能越好，所得到的谐波信号越精确，但是还需根据实际系统选择滤波器的阶数。在滤波器阶数过大的情况下，不仅得到的谐波幅值与对称度较小，还会导致谐波信号中心波数发生偏移。如图9(a)中滤波器阶数超过12后，谐波信号受到残余幅度调制带来的干扰，使得信号峰谷难以辨别，给整个TDLAS系统的检测带来较大的影响，相对于文中测量系统来说，取5阶巴特沃斯低通滤波器可以得到较高的谐波幅值以及对称度，能够得到较高辨识度的谐波信号。

4 谐波优化仿真实验

经上述研究，得出了各参数的优化结果，下面通过优化一组二次谐波曲线来展示优化步骤。

图10(a)为一组未经优化的二次谐波信号，生成此信号的调制度为0.000 5 V、调制频率为1 000 Hz、扫描幅度为0.040 V、扫描频率为10 Hz、低通滤波器阶数为7阶。

图10 优化前后二次谐波的对比

图10(a)中谐波信号幅值较小且不完整，并伴随信号失真现象。为了获得完整的谐波图像，首先改变扫描幅度为0.068 V，使得红外激光完整扫过气体吸收峰，同时选择5 Hz作为扫描频率，使每周期采集信号点数提高，优化后的谐波图像如图10(b)所示；观察图10(b)发现，图中仍然存在部分谐波信号失真问题，此时降低滤波器阶数至5阶以减小谐波失真问题，并提高调制频率至2 200 Hz，得到的谐波图像如图10(c)所示；最后提高调制度至0.010 V，以增加谐波的信号强度与峰宽，优化完成的谐波信号图像如图10(d)所示。

提取图10中谐波的特征值，如表1中所示。分析可得第一、第二次优化主要是增加谐波完整性与消除波形失真现象，第三次优化(即增加调制度)能够有效增大谐波幅值与峰宽。

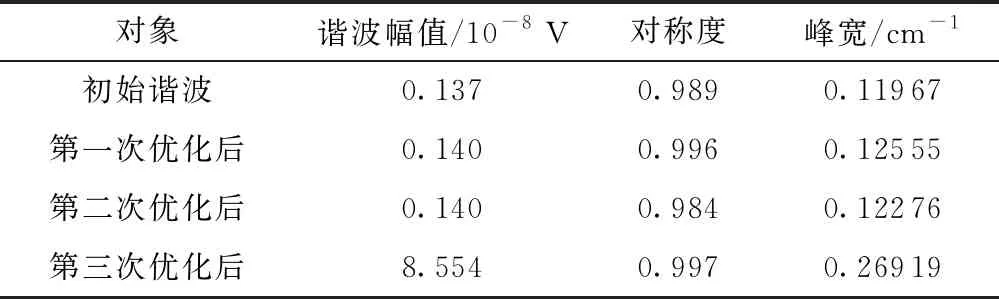
表1 优化前后谐波特征值的对比

5 结语

文中研究了TDLAS系统不同参数对二次谐波的最大幅值、对称度、峰宽的影响。研究表明，对于一般TDLAS检测系统，应优先选择合适的扫描幅度与滤波器阶数，使得谐波波形完整且不失真，以保证检测结果的有效性；然后尽可能增大谐波幅值与峰宽，得出最佳调制度；最后根据系统需求和自身硬件基础，选择合适的调制频率和扫描频率。该研究结论可广泛应用于光谱学TDLAS检测领域，可为研究者们在TDLAS系统的搭建过程中根据需求选择实际技术参数提供依据。