分类思想在中职数学教学中的渗透

俞祥龙

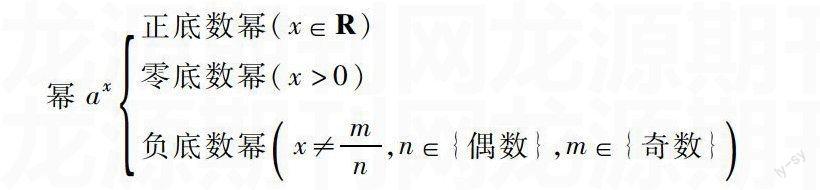
【摘要】数学思想方法隶属于中职教材，融合和隐藏于数学知识体系中.作为常见的分类思想，教师要根据中职生思维特点和认知水平，在教材中挖掘，在概念、判断、推理中揭示，帮助学生领悟和提炼.分类思想在中职数学教学中的渗透遵循循序渐进、逐步渗透、螺旋上升的原则，有助于学生形成良好的认知结构和有助于把这种分类思想迁移到以后的工作生活中去.

【关键词】分类思想 ；理性思维；渗透

数学思想和方法是数学的精髓和灵魂，其中分类思想在社会生活中、小学初中数学中普遍存在，如“物以类聚，人以群分”“合中分，分中合”，实数的分法和趣味题目“树上停着10只鸟，猎人打中了1只，树上还有几只鸟？”等等.分类思想不管是在教学中，还是高教版教材中和中职大纲中都隐性地存在着，所以，我们应结合中职生的思维特点，更多从教材中、教学中把分类思想显性化，提高中职生学习数学的趣味性，培养中职生思维的条理性、逻辑性，甚至为以后工作和生活提供指导，增强迁移能力.

所谓分类思想，就是根据数学本质属性的相同点和不同点，将数学研究对象分为不同种类的一种数学思想，又称逻辑划分.一般按照“明确对象——确定标准——逐类讨论——归纳总结”的思维步骤来分析问题.本文从以下几点分析分类思想在中职数学中的渗透.

1.处理教材，挖掘分类思想

中职高教版数学等数学教材内容一般只显示数学知识，而蕴含于知识中的分类思想方法没有点明或为了避免分类讨论而不采用分类思想方法.概念、性质、法则、公式、定理等知识是数学的外在表现形式，而分类思想等数学思想属于内隱形式，隐藏在数学知识背后.教师应通过处理分析教材，挖掘分类思想，体现数学本质.“授人以鱼不如授人以渔.”很多数学知识，等到学生走上工作岗位就忘记了，而数学思想方法、数学逻辑思维却会自觉不自觉地应用与迁移到工作生活中.分类思想是贯穿整个中职数学的一种重要思想，几乎涉及每个知识点.因此，在中职数学教学中，制定教学目标，既要体现数学知识，又要在适宜时机体现分类数学思想.

比如，中职高教版数学高一教材中，对解绝对值不等式只用了绝对值的几何意义来分析，如|x-1|<2，把x-1 看作整体，其到原点的距离小于2，得-20两种情况讨论；或对左边的式子x-1的正负性讨论，分x-1≤0和x+1>0两种情况讨论，然后把两类的结果合并综合.导致这题错解的原因，就是平时教师根据教材来教，解题方法的唯一性或不注意口诀的前提条件而导致思维的定式.因此，在讲授新课时候，要尊重中职生的思维能力不强、数学基础总体薄弱、高一学生正从感性认识向理性认识转变的特点.对解绝对值不等式，可分三种情况|x|<2，|x|<0，|x|<-2来分析，从而得出：|x|0，|x|

再比如，中职高教版高一教材中，对解一元二次不等式只结合一元二次函数的图像来分析.如ax2+bx+c>0a>0，令fx=ax2+bx+c，根据图像可得不等式的解.虽然数形结合的方法比较容易，但过了一个学期，总有些数学基础中等偏下的同学对原解法理解不深刻或口诀只会生搬硬套而不会解了.因此，建议在教学中一题多解、扩散思维，对一元二次式因式分解后再对两个式子的正负性进行讨论分析，一方面可以比较两种方法的优劣，另一方面可以渗透分类思想.

从这两个例子可以看出，教师在教学工作中教好教材，更要用好教材，挖掘和提炼数学思想方法，并在教学中渗透分类等思想方法，有助于培养中职学生数学兴趣和提升思维的缜密性、深刻性.

2.形成概念，体验分类思想

数学概念是人脑对现实对象的数量关系和空间形式的本质特征的一种反映形式，即一种数学的思维形式.数学思想方法是数学知识的重要组成部分，基于数学内容又高于数学内容的一种隐性知识，往往以隐藏的形式渗透在概念发生、发展、形成过程.下面就举几个概念中体现分类思想的例子：

中职高教版数学教材对实数指数“幂”概念形成过程很简单，“幂”这个概念最早是在乘方运算中提出来的，即相同因数连乘积的运算叫作乘方，结果称为幂.幂的两个要素为指数与底数.底数的取值范围由任意实数随着指数的拓广最后限定为正数；指数为正整数时也称个数，指数从正整数推广到整数，有理数再到实数.最后，幂随着指数的变化为确保幂的存在而对底数进行限定才形成实数指数幂.通过以上分析可知，幂形成的两个要素为底数和指数，而这两种实数都可以从范围来分，也可以从正负性来分.而教材上没有实数指数幂形成过程的说明，也没有幂的分类图，所以，建议为了对“幂”这个概念有一个整体的认识，可以从两个角度四个方面去划分幂，为了更好地突出幂的应用广泛性和引入幂函数的需要，根据指数的范围给出如下的一个分类图（根据指数的范围）：

当然，若从指数正负性来划分：实数指数幂可以分为正指数幂、负指数幂和零指数幂.若底数从实数范围划分，实数指数幂也可以分为有理数底数幂和无理数底数幂.若底数从正负性划分，则可以得到：

幂ax正底数幂（x∈R）

零底数幂（x>0）

负底数幂x≠m[]n，n∈{偶数}，m∈{奇数}

以上两种角度四种方法的分类，都要根据一个确定的、统一的标准来分，分的标准就是概念的要素，多个要素可以确定多个分类.通过分类，可以使概念系统完整，从而达成这个概念体系，在概念的形成中和体系的搭建中渗透分类思想.

3.探究原理，揭示分类思想

中职数学教科书由于篇幅限制和中职学生的学习特点，往往只有公式、定理的简略的推导过程或现成的结论，因而要引导和鼓励学生探究原理和揭示原理背后的思想方法.

数学原理是对数学概念之间稳定不变的关系的描述，数学概念是数学原理的基础.如高教版中职拓展教材中直接给出两个计数原理，没有对原理进行探究分析.计数原理的基础涉及两个基本概念：加法和乘法.本校学生在本区内数学基础是中等以下的，很多学生对分步完成乘法原理的理解只是停留在公式套用的层次上，原因在于一方面对分步完成还是分类完成分不清，另一方面对分步完成为什么用乘法原理的理解没有本质的认识.现举例分析：

例1 甲地到乙地有2条路可以走，分别记作a和b；乙地到丙地有3条路可以走，分别记作c，d，e，那么从甲地经过乙地到丙地共有几种走法？

分析 若甲地到乙地选择a，则有ac，ad，ae共三种走法；若甲地到乙地选择b，则有bc，bd，be共三种走法，总计3+3=2×3=6种方法.

例2 在例1基础上现增加从丙地到丁地有4条路，分别记作f，g，h，j，问从甲地经过乙地和丙地最后到达丁地共有几种走法？

分析 从例1可知甲地到丙地有2×3=6种，若最后一阶段从丙地到丁地选择了f，则甲地到丁地有6种，同理若选择了g，h，j也分别有6种，所以共计6+6+6+6=6×4=2×3×4=24种走法.

从以上两个例子分析可以看出：分步完成乘法原理的分析用到了分类思想，对每个阶段出现的路进行分类讨论；分步完成乘法原理的基础是分类完成加法原理，就如乘法运算是指将相同的数加起来的快捷方式，乘法的基础是加法一样.因此，对分步完成用乘法原理的不深刻理解源于对乘法运算的含义理解的肤浅，而这个最简单、最常见的乘法原理却蕴含着分类的思想，在探究原理的过程中，揭示分类的思想.

4.解决问题，领悟分类思想

例3 已知x∈R， n∈N*，求数列xn的和：Sn=x+x2+x3+…+xn.

分析 由于x的任意性，本题未指明数列为等比数列，所以要考虑该数列是等比数列和不是等比数列两种情况，而其中等比数列又要分公比為1和不为1的两种情况.总之，分类讨论时要考虑分x=1，x=0，x≠0且x≠1共三种情况分析求解.

例4 已知A={1，2}，B={xmx=1，m∈R}，BA，求m的取值范围.

分析 B是A的子集，B要分空集和非空集共两种情况.其中B为非空集时，要考虑B为单元素集合和双元素集合，排除双元素集合，又有B=1，B=2共两种情况.

例5 有5名同学排成一行拍照，甲同学不排在最左边，乙同学不在最右边，问有几种排法？

分析 先考虑甲同学.如果甲同学在最右边，余下的4名同学的排列不受限制，一次有A44种排法；如果甲同学不在最右边，则只能排在中间3个位置，此时乙同学也只有3个位置可以选择，因此有A13A13A33种排法.所以，共有A44+A13A13A33=78种.

解决以上数学问题，实质是变换命题形式和分类思想的反复运用.比如，例1的步骤：明确对象（集合B）——确定分类标准（集合B元素的个数）——逐类讨论（空集，单元素集，双元素集）——归纳总结（所有的情况合并得出m）.对所求的m不能统一进行研究，变换命题的形式分析集合B，然后再分类，最后得出m的值.此类数学问题的每一步转换，都遵循着分类思想方法“总——分——总”的规律.通过这类数学问题的解决，会避免分类中重复和遗漏的现象，学生能够领悟分类的魅力.

5.整合知识，提炼分类思想

数学思想方法隶属于中职教材，融合和隐藏于数学知识体系中.因此，根据中职生思维特点和认知水平，当教学中涉及分类思想时要在整合数学知识过程中提炼分类数学思想，引导学生从分类数学思想的高度去总结、归纳、深化.对于最常见的分类思想，可从生活现象中的分类迁移到数学中的分类，遵循循序渐进、逐步渗透、螺旋上升的原则，适时归纳一些常见的分类思想方法和分类的一般步骤，从而有助于学生形成良好的认知结构和有助于把这种分类思想迁移到以后的工作生活中去，真正达到我们教数学，学生学数学的目的——学好数学知识点，更要培育理性精神和掌握数学思想方法.