谈小学数学挑战性练习的设计与教学
何月丰
[摘 要]积极、深刻地思考是学生思维活动发生的前提。具有挑战性的练习是诱发学生积极、深刻思考的重要载体。设计挑战性练习时,可以将给学生铺垫的台阶移除,可以将分散的小问题整合,可以将显性的条件隐蔽,可以将正面的问题反问。挑战性练习教学时,问题呈现要清晰明了,过程控制要科学合理,反馈顺序要梳理到位。
[关键词]数学 思维 思考 练习设计 挑战性
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2015)14-007
培根说:数学是思维的体操。可见数学是锻炼人的思维最好的载体。思维的锻炼依赖于思维活动的发生。其中,引发“思考”是驱动思维活动产生的前提。因此,在数学教学中,诱发学生积极主动、深刻地思考是锻炼学生思维的有效途径。
维果茨基的“最近发展区”理论揭示:教学应着眼于学生的最近发展区,为学生提供带有难度的内容,调动学生的积极性,发挥其潜能。“带有难度的内容”对学生而言是具有一定挑战性的。面对具有挑战性的内容,就需要学生积极主动地、深刻地思考,发挥潜能,实现“跳一跳摘桃子”。
将上述两者结合不难发现,在数学教学中,设计具有一定挑战性的问题(包括练习),是诱发学生主动深刻思考、锻炼思维的有效策略。
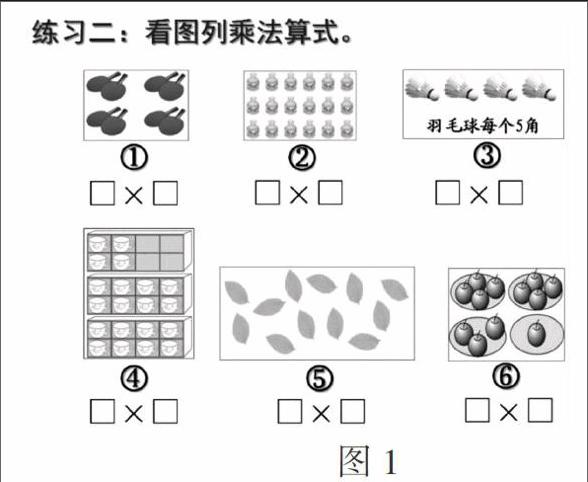
练习是小学数学教学的重要组成部分,它主要承载着“巩固和熟练所学”的功能。基于这个目的进行的练习是必要的,但若仅为此而练,学生难免就会陷入“机械解题”的泥潭。例如二年级的“乘法的初步认识”,教材在这一课的练习中,为学生提供写乘法算式的材料一般都是“成品”,即“相同加数是几”和“有几个相同加数”都是可以直观看出来的。一直做这样的练习,学生到后来“站着就能摘到桃子”,不能充分激发学生思考的兴奋度,学生也就难以产生深刻的思维活动。因此,在这一课练习的后续环节,我们设计了一个具有挑战性的练习(如图1)。
在这个挑战性练习中,“相同加数是几”和“有几个相同加数”变得不再直观,需要学生通过积极深刻的思考,借助分一分、圈一圈等方法来解决。学生在这样具有个性化的思维活动中,不仅创造出了“相同加数”及其数量,还进一步加深了对乘法本质意义的理解,思维能力得到了有效提升。
可见,在小学数学练习教学中,除了扎实必要的基础性练习之外,设计一定的挑战性练习,可以诱发学生积极主动、深刻地思考,提升学生练习时思维的参与度。
一、挑战性练习的设计策略
挑战性练习的设计,一般途径有两条:一是对教材原有习题进行改编,二是基于教学需要进行创编。不管是改编还是创编,其设计策略,可从以下几方面入手。
1.移除台阶——从平稳拾级到用力攀登
挑战性练习,需要学生“跳一跳摘桃子”,因此在设计练习时,就需要考虑移除层层铺垫的小问题(台阶),让学生直面具有挑战性的问题,在“用力攀登”中锻炼思维能力。
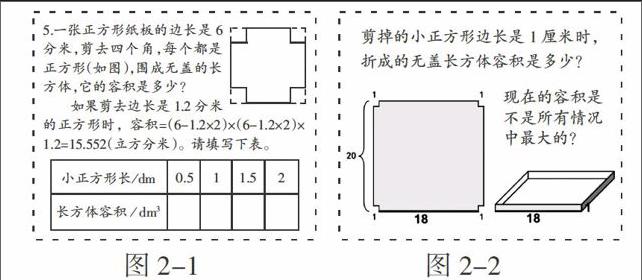
如图2-1是浙教版五年级下册“练一练十三”中的一道习题。
这个题目有两个目的,一是让学生理解将一张正方形纸四个角都剪掉一个小正方形后,折成无盖长方体的容积计算方法;二是让学生在进一步熟练这样的计算的过程中,发现容积大小的变化。因为这里涉及从平面到立体的转化,学生必须要通过思考厘清其中的变化,找到需要的条件。然而这些可以让学生积极思考的地方,题目都为学生搭好了台阶——给出具体的计算样例,学生只要按照步骤计算即可,过程成了机械的程序操作,思考度明显淡化。
基于这样的理解,我们对这个练习进行了改编设计(如图2-2)。
第一,先让学生自己独立思考:将一张正方形纸4个角都剪掉1个边长为1厘米的小正方形后,能折成什么?进一步思考折成的无盖长方体容积的计算方法,这里学生需要将其与原来的正方形纸进行对比,努力寻找需要的条件,思维将得到挑战和锻炼。
第二,在上述基础之上,继续追问:“现在折成的无盖长方体的容积是不是所有情况中最大的?”面对这个问题,学生需要经历猜想、验证、观察等过程,在熟练计算方法的过程中锻炼了思维能力。
如此设计,移除了为学生解决问题而层层铺设的台阶,让学生不能平稳地拾级而上,需要跳一跳或者自己寻找台阶,在接受挑战的同时提升思维能力。
2.抓大放小——从点对点练习到大问题引领
一般的练习,往往是点对点的,即一个问题练习一个知识点。综合问题,一般是分成几步或若干小题的练习,综合在一起形成一个大问题,给学生更为开阔的思考空间,提高问题的思维挑战性。
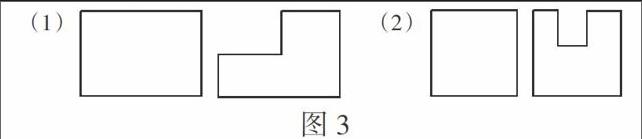
如图3是人教版三年级上册练习十八中的一道习题。
原题将“周长一样”和“周长变长”两种情况以两个小题的形式呈现,一个小题解决一种情况,并都以两图对比的形式呈现,练习呈现“点对点”的特征。学生在解决问题的过程中,思维是直线式的,通过观察基本能得出结论,思考兴奋度得不到充分激发。
基于这样的想法,我们将原题进行修改:
在一张正方形纸上剪去一个小正方形,剩下图形的周长与原来正方形的周长比较,会发生怎样的变化?
如此设计,就将原题中的两个小题合并到了一个问题,以大问题的形式引领学生展开思考,增加了思维的挑战性。学生在解决问题的过程中需要想一想、剪一剪,在对比、观察中学生的思维能力就能得到更好的锻炼。
3.化显为隐——从直观利用到自主寻找
一般的数学问题,都比较“规范”——现实情境经过了提炼和加工,条件在变得充分且必要的同时,也显得直观。学生只要依据提供信息就能找到方法和答案。挑战性练习,需要改变问题的呈现形式,将显性的条件隐性化,逼迫学生通过思考,自主寻找与练习相关的知识和方法来解决问题。
例如四年级“积的变化规律”,一般的练习是给出一个已知算式,然后根据已知算式运用积的变化规律填空,如“已知A×B=150,那么(A×2)×B=( )。”这样的练习是需要的,但只是这样的练习显然思考力不够,因此,在后续的练习课中,我们设计了一组“口算”练习(如图4)。
教学时,课件依次出示口算题,要求学生快速口算。有了“快速口算”这个要求作为驱动,学生就会自主地思考因数与因数之间的变化,并依据这样的变化得出积,这就是对“积的变化规律”的创造性运用。
在这里,我们对“因数变化”进行了隐性化处理,突破了“规范”,而学生的思考力就在这样的“非常规”中得到锻炼。
4.正反交融——从正向运用到逆向思考
运用所学知识正向解题是练习的基本模式,挑战性练习可以改变这样的模式,尝试从反面切入,让学生在逆向思考中锻炼思维能力,加深对知识本质的理解。
例如“负数”一课的练习,一般是给出一个具体的负数让学生解释其实际意义,如银行卡上出现的负数,学生会解释为“表示取出”。我们认为,这样给出一个存在的负数让学生依据生活经验来解释,思维冲击不够,难以体现创造性。对此,我们设计了反向的运用练习。
下面几种生活中的情况,有没有可能也要用到负数来记录的呢?银行卡里的钱;某地的海拔高度;小强的身高;风的速度。
先让学生独立思考,然后小组交流。下面是某个小组的交流情况:
●钱不可能是负的,用完了就是0。
●取钱就有可能是负的;
●海拔有可能是负的,有些地方比海平面要低;
●身高不可能是负的,人生下来就有高度了;
●风速不可能是负的,最多没有风,那是0。
在学生小组充分交流的基础上开展全班交流:
●钱可能是负的——两种情况:取钱、透支;
●有些盆地比海平面低,海拔就是负的;
●冰岛三分之二的面积在海平面下面,他们的国家要修筑堤坝的;
●人老了会变矮,就是负的;
●把昨天的风速作为标准,今天比昨天快就是正的,比昨天慢就是负的。
从小组交流到全班交流,学生的思维得到了充分的激发和锻炼,在进行这样思考和对话过程,学生对负数本质的把握也越来越深刻。
二、挑战性练习的教学策略
习题价值的最大化,依赖于有效的运用,挑战性练习也是如此。在进行挑战性练习具体教学时,我们需要做好以下几点。
1.问题呈现要清晰明了
学生对挑战性练习的题意的理解,相比于一般的基础性运用练习,难度会大一点。这就要求教师在呈现挑战性练习时,要做到清晰明了——明确条件是什么和问题是什么,防止学生不明题意或产生歧义,进而影响练习的效果。
第一,练习在呈现时可“动静结合”。即条件和问题可以一条一条出示,让学生逐条理解,提高清晰度。
第二,练习在呈现时可“适度支撑”。即在呈现练习本身信息的基础之上,可适度提供一定形式的支撑(如文字配图形,图形配文字),帮助学生更好地理解题意,明确方向。当然,这里需要强调适度,例如上例中的“在一张正方形纸上剪去一个小正方形,剩下图形的周长与原来正方形的周长比较,会发生怎样的变化?”可以出示正方形图片“支撑”,帮助学生理解,但不能演示小正方形的剪法,否则就是过度“支撑”,会降低思考性。
2.过程调控要科学合理
挑战性练习,学生在明了题意之后,往往不能立刻解决,并且解答的过程也会相对较长,这就需要教师在学生解答过程进行科学合理的调控。
第一,一般建议学生读题后先不要急着动笔,而是要先想一想,如“题目让我做什么”,“我可以怎么做”,等等。
第二,在学生独立解答过程中,教师要观察学生的解答情况,适当给予个别指导,或针对一个大家都碰到的困难,适时给予提醒,还可根据实际安排小组讨论。
3.反馈顺序要梳理到位
具有挑战性的练习,学生的解答过程更为丰富,生成的材料更为多样。面对多样的生成材料,有序合理的反馈可以进一步提升练习的价值,提升学生的认识。
第一,练习前要想清楚学生可能会生成怎样的材料。这些材料哪些是要反馈的,哪些是不要反馈的,哪些需要重点反馈,哪些可以简单反馈。
第二,练习的反馈应适度有别于新知探究的反馈。新知探究的反馈重在呈现知识的形成过程,需要正面、反面的例子,往往会面面俱到。练习的反馈一般不需要面面俱到,只要找到典型即可。
第三,在学生解答过程中,要收集学生的实际解答情况,并与自己的预设进行对比,如果出现与预设不符的,可利用 “借鸡生蛋”,或通过学生的方法进行转变等呈现方式。
著名特级教师孙四周说:“上帝没有给我翅膀,我却用自己的思考飞翔。”思考的力量让他在数学教育领域取得了辉煌的业绩。同样,我们也应该在小学数学教学中让思考多飞一会儿,让学生借助思考来飞翔。
(责编 金 铃)

