渗透数学对应思想 夯实数学思维基础
吕健威
[摘 要]小学数学的不少内容都有知识上的对应关系存在,因此,教师可以利用对应思想来指导学与教。认识和利用数学对应思想,要由浅入深、由具体到抽象,逐步形成自己的数学思想方法。课堂教学中,教师要把培养学生的对应思想作为数学教学的基本要求,最终达到发展智力、培养多种思维能力的目标。
[关键词]对应思想 渗透 思维方式 夯实
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2015)14-042
数学中的对应是指人的思维对两个集合间联系的把握,“一一对应”的意思就是在这两个集合中存在一个对一个形成一种相呼应的状态。教学实践证明,要找到解决问题的切入点,关键要找到谁对应谁,即对应的联系点,问题将迎刃而解。数学对应思想是一种重要的数学思维方式,在数学中处处存在并被运用。培养学生的数学对应思想是基本的教学要求,对提高学生的计算、分析、解题、作图等能力有重要作用,为学生数学思维的形成奠定基础。
一、数形对应思想的渗透
在小学数学教学中重视数形对应思想的渗透,不仅能化难为易,帮助学生理解数学概念和掌握数学技能,而且能潜移默化地使学生养成数形对应的习惯,为进一步理解和发展数学对应思想打下基础。
1.在用图解法解应用题中渗透对应思想
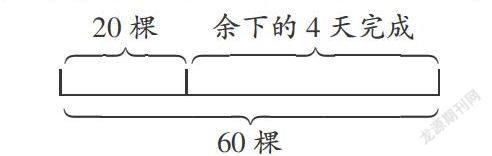
线段图能准确、明了地展示题中的数量关系,因此,用对应思想分析线段图中的信息,能正确、快速地解决问题。如:“学校计划植树60棵,今天已植树20棵,余下的在4天完成,余下的平均每天植树多少棵?”
“60棵”“20棵”和问题都不对应,而“余下的棵数”与问题对应。在找到已知与问题的基础上,首先要找对应,让学生根据问题找到与问题相对应的条件,这样就能把复杂问题简单化,同时让学生掌握分析问题、解决问题的方法。
2.在几何概念中渗透对应思想
在三角形中,有什么样的底,对应什么样的高,这就是底与高的“一一对应”。
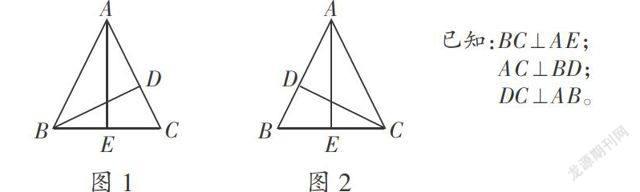
问题:如下图,求出三角形的面积(单位:厘米)。
用BC×AE÷2或AC×BD÷2求三角形的面积是对的,而BC×BD÷2是错的,原因是BC底边与BD不对应,只有找准对应才能列对式子。语文知识上的“底”和“高”的意思跟数学概念上“底”与“高”的含义是有所区别的,运用对应思想会进一步加深对概念的理解。
二、函数对应思想的渗透
如果对于任意的x的值,有完全确定的y的值与之对应,那么称y为x的函数。这里可以看出,函数思想的本质是对应。因此,教师在指导学生学习数学时,要心中有函数思想,可以利用一些具体的例子,找准哪个量不变,让某个量“动”起来,或者一个量变化,另一个量也随之变化,引导学生看出运算结果是随着哪一个量的变化而变化的,进而从中找出对应关系。
1.在比的知识中渗透对应思想
比的前项和比的后项是两种相关联的量,实质上就是函数关系(多元函数情况)。例如,在解决“按比例分配”的问题中,一般来说,已知比的总数量,学生比较容易解决,已知部分数量(或相差量),学生比较难解决,而找准已知数量与比中的哪个项相对应是关键。如“男生人数和女生人数的比是5∶6”,即男生人数对应5,女生人数对应6;如果男生有20人,那么比的前项5对应男生20人,女生人数就是20÷5×6=24(人);如果全班有44人,那么44人对应的是比的前项与比的后项的和,即女生人数是44×6/5+6=24(人)。对应找对了,问题就会轻松解决,也增加了解决问题的乐趣。
2.在四则运算中渗透对应思想
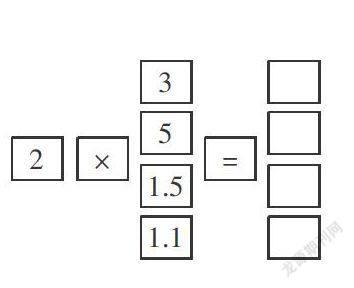
小学数学课本中有填数图、韦恩图等内容,并将函数概念渗透在许多例题与练习中。例如,人教版数学五年级上册第6页练习(如右图):当一个因数固定不变时,积随着另一个因数的变化而变化。类似的题就计算而言没什么难度,关键是教师在教学这些习题时,要心中有函数思想,可以利用一些能移动的卡片,引导学生从片卡的变化中找出数量对应关系。
3.在几何公式中渗透对应思想
小学数学中几何图形的面积公式和体积公式,以函数的观点来看,实际上就是用解析法来表示变量之间的函数关系。如长方体的体积V=abh,其体积随着长、宽、高的变化而变化;圆的面积S=πr2,其面积随着半径的变化而变化;一个长方形的面积一定时,一条边随着另一条边的变化而变化……这些公式渗透了幂函数和多元函数的思想。
三、空间对应思想的渗透
1.在“拳头”与“月份”中渗透对应思想
课堂教学中,教师可引导学生将熟知的事物和某个数学知识产生联系,实现事物与知识的对应及对新知的认知和理解。如拳头的凸凹位与月份名称有着对应的巧合,有的教师没有强调这个关键处,使学生误以为拳头含有月份名,造成理解障碍。教师应告诉学生,借助拳头的凸凹位记大月、小月的知识是一种记忆方法,其中拳头的凸凹位与大月、小月是一种对应关系。如随便一只手握紧拳头且手心向下,数手指与手掌相连的那个关节,从食指起,食指凸出的关节为一月,食指与中指间凹进去的部位为二月,中指凸出的关节为三月,中指与无名指凹进去的部位为四月……重复数这只手从食指起,食指凸出的关节为八月,无名指凸出的关节为12月。凸对应大月,有31天;凹进去的部位对应小月,有30天;2月为特殊月,平年的二月有28天,闰年的二月有29天。
2.在数对知识中渗透对应思想
小学数学空间对应的内容比较欠缺。事实上,教师排座位,在黑板上列一个座位表,下面的学生根据座位表找到自己的座位,这就是空间对应。例如,教学“用数对确定位置”的例1(多媒体出示图表)时,学生根据小红在教室的第3列、第1行用数对(3,1)表示,初步建立与座位示意图的对应关系;在同样的规则下,再次通过小荣坐在教室的第5列、第2行怎样用数对表示和给出数对确定位置的活动,加深学生对数对和座位示意图列与行的一一对应关系。这样教学既有利于学生直观体会直角坐标系的思想,又通过方格纸研究几何图形的有关特点和性质,获得几何活动经验,发展几何观念,逐步培养了学生推理的意识和能力。
根据学习《数学课程标准》所得及多年的实践体会,小学数学的不少内容都有知识上的对应关系存在,所以教师应该利用对应思想来指导学与教。教师首先认识和利用数学对应思想,引导学生从数与实物、线、图形、数量关系、空间等各元素之间产生的元素和元素的对应关系开始,由浅入深、由具体到抽象,逐步形成自己的数学对应思想与具有自觉用数学对应思想的思维品质,最终达到多种思维齐发展和夯实学生数学思维的目的。
(责编 蓝 天)

