谈对应思想及其在数学教学中的渗透
龚焕淼

[摘 要]小学数学中蕴涵着丰富的数学思想方法,对应思想是其中之一。运用对应思想实际上就是寻找可以对应的联结点,找到一条通向已经解决的问题的途径。根据小学生的学习特点,教师在教学中应以具体数学知识为载体,重视对应思想的渗透,引导学生领会对应思想,揭示其内在的本质与联系,从而提高学生解决问题的能力,发展他们的数学思维。
[关键词]小学数学 对应思想 渗透
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2015)14-044
小学数学教学内容中有两条线索:一条是显性的知识线索,如概念、公式、性质等;另一条是隐性的数学思想方法线索,它蕴涵、渗透在知识体系之中,是一条无形的线索。小学生由于能力、心理发展等方面的限制,往往只注意数学知识的学习,而忽视联结这些知识的思想与方法。因此,数学教学中,教师要在抓住知识线索这条明线的同时,还要紧紧抓住隐含在数学体系中的思想方法的这条隐性线索,为学生未来的发展奠定良好基础。
一、对应思想的内涵
对应思想是人们的思维对两个集合元素之间联系的一种思想方法。也就是说,一个系统中的某一项在性质、作用、位置上跟另一个系统中的某一项相当,形成一种相呼应的状态,其本质是一一对应。
渗透对应思想的核心是使学生感悟到寻找对应关系的方法,以对应的观点对所要解决的问题进行转换,其关键在于找到可以对应的联结点,找到一条通向已经解决的问题的途径,这是对应思想的精髓所在。也就是说,当遇到较为复杂或隐蔽的问题时,通过对应的方法找出对应的关系,化抽象为直观、化难为易、化繁为简、化隐蔽为明晰,从而使问题得以顺利解决。对应作为一种重要的数学思想方法,隐藏在整个教材之中,许多具体的数学方法都来源于此,是应用最普遍的数学思想方法之一。
二、对应思想在数学教学中的渗透
1.在知识形成中充分感悟——引导学生体验对应
著名儿童心理学家皮亚杰的认知发展理论表明,6岁的孩子已经有了对应的意识。虽然小学低段数学知识比较浅显,但也蕴含着丰富的思想方法,所以教师在小学一年级时就可以渗透对应思想来指导学生的学习。只有让学生从小接触对应思想,才能在以后的数学学习和应用中熟练运用对应思想,提高学生解决问题的能力。
对应思想蕴含于生活之中,如一个学生对应一个学号、一支铅笔或一本书对应一个抽象的数字“1”等。对应思想也蕴含于数学知识的形成过程中,如“看图写算式”“多位数乘一位数”中利用数形对应理解数与式的概念、利用数轴渗透点与数集的对应把数轴上的点和数建立一一对应的关系等,都是渗透对应思想的好素材。在学习这些数学知识时,教师要尽可能提炼出蕴含其中的对应思想,在知识产生、形成过程中,让学生充分体验。
例如,教学一年级“比一比”时,为让学生通过操作初步建立起“同样多”的概念,教师引导时有以下两种策略:一是数数;二是进行配对,即用一一对应的方法比较物体的多少。如小兔搬砖,一只小兔搬一块砖,即一只小兔对应一块砖,正好都对应上,没有多余的,所以小兔和砖就是“同样多”。配对时可上下一一对齐,再用虚线相连来强化对应。在这个过程中,学生初步感知了对应这一思想在数学学习中的运用。
在接下来“比大小、比多少”的练习中,对应思想也有所体现。如下面这道练习题:
教学时,教师可借助多媒体先出示7个三角形,让学生数一数,再在三角形后面紧跟着出示10个小圆形,然后出示问题,让学生思考好后说说自己的想法。这时,学生当然采用先数数再计算的方法。在此基础上,教师把右边的10个小圆形移到三角形下面,使10个小圆形通过移动逐渐与三角形一一对应起来,并显示对应的小圆点,然后让学生说说画面有什么变化、这样排列有什么好处。通过对比,让学生感受到两种物品对应起来一眼就能看出多多少、少多少。同时,教师还可以让学生借助圆片和三角形,让学生像这样对应起来摆一摆、说一说。通过以上教学环节,使对应的方法真正被学生接受,在以后遇到类似的问题时,就自然会用一一对应思想来思考和解决问题。
2.在实践中加强探究——引导学生初步运用对应
通过一定的体验学习,学生已对对应思想有了一个初步的感知和认识,在接下来的学习中,教师要找准契机,引导学生初步运用对应思想,逐步培养学生用对应思想解决问题的能力。
例如,“面积和体积”的教学是先通过转化,将未知图形变换为已知图形,引导学生观察转化前后两种不同图形之间的对应关系,从中建立起不同图形之间的对应关系,再通过已知图形面积、体积的计算方法,推导出未知图形面积、体积的计算方法,使学生在观察、比较、对应、推导中找到解决新问题的思路。
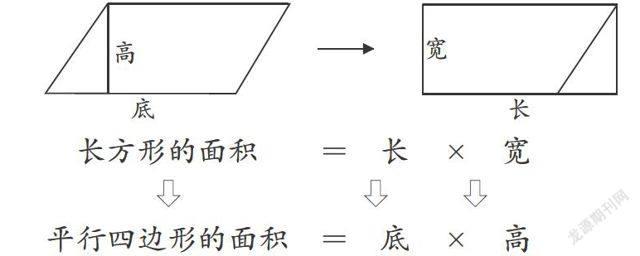
又如,在平行四边形面积公式推导过程中,对应思想也深深蕴含其中,即把平行四边形转化成长方形后,转化前后的两种图形在多处体现了对应关系。如下:
如上图所示,长方形面积与平行四边形面积相对应,长方形的长与平行四边形的底相对应,长方形的宽与平行四边形的高相对应。在此对应的基础上,平行四边形的面积计算公式才得以推导出来。
而在探究三角形的面积、梯形的面积和组合图形的面积时,都是以长方形面积计算为基础,以图形内在的对应联结点为线索,以未知向已知转化为基本方法开展学习。此外,利用长方形面积计算方法推导圆面积计算公式、利用长方体体积公式推导圆柱体积公式等,无不体现着对应思想。
3.在问题解决中及时提炼——引导学生灵活应用对应
到了小学高段后,学生已对对应思想形成了一定的认识基础,但只有进一步的运用,才能将所学知识内化为学生自己的东西。教师可让学生用掌握的对应思想去分析与解决问题,使学生从数学思想方法的高度把握知识的本质,让对应思想在学生心里扎根,逐渐转化为学生内在的一种能力。
例如,在“植树问题”教学中,教师可用对应思想统领整节课,充分地创设各种问题情境,利用点(种树棵数)与段(间隔)的一一对应,让学生在观察、比较、类推中,深刻地理解种树的棵数与间隔数之间的关系,从而建立解决“植树问题”的一般模型。
小学数学中蕴藏着各种可运用对应思想进行解答的内容,教师应重视在平时的教学中,以具体数学知识为载体,有意识、有针对性地进行教学,引导学生领会蕴含其中的数学思想方法,揭示它们的本质与内在联系。若干年后,数学知识可能被遗忘,但相应的数学思想方法会一直伴随着学生,使其一生受益。
(责编 杜 华)

