基于初、高中衔接的“二次函数”教学

☉江苏省徐州市第五中学 王运思

基于初、高中衔接的“二次函数”教学

☉江苏省徐州市第五中学 王运思

函数是初等数学主要学习内容之一，它贯穿了整个中学阶段的数学学习.初中数学主要学习一次函数（正比例函数）、反比例函数和二次函数，其中二次函数是初、高中函数学习的一个重要衔接点，因此做好二次函数的初、高中衔接教学至关重要.初中阶段对二次函数的要求，还是立足于用代数方法来研究，比如配方、结合顶点式描述函数图像的某些特征（开口方向、顶点坐标、对称轴、最值）等；再比如待定系数法，通过解方程组的形式来求二次函数的解析式.少量涉及了数形结合内容，如通过画图像找增减性、开口方向、最大或最小值，以及通过图像了解二次函数与坐标轴的交点及一元二次方程的根之间的关系等.可见初中对二次函数的要求相对较低，而高中的函数立足于“集合说”，函数的概念更为抽象，对函数的研究更为深入和广泛.进入高中后，对二次函数的学习要求明显较高，对二次函数的研究更侧重于数形结合，通过图像来研究性质，要求“数化形”及“形化数”的能力较强.那么，究竟该如何衔接好初、高中二次函数的教学，让学生进入高中以后，能够很快适应高中的大容量、快节奏教学方式？为此，笔者进行了一些思考与尝试，现举例说明如下.

一、函数图像的平移

例1把二次函数y=x2+bx+c的图像向上平移2个单位，再向左平移4个单位，得到函数y=x2的图像，求b、c的值.

解法2：把二次函数y=x2+bx+c的图像向上平移2个单位，再向左平移4个单位，得到函数y=x2的图像，等价于把二次函数y=x2的图像向下平移2个单位，再向右平移4个单位，得到函数y=x2+bx+c的图像.

由于把二次函数y=x2的图像向下平移2个单位，再向右平移4个单位，得到函数y=（x-4）2-2的图像，即y=x2-8x+14的图像，则函数y=x2-8x+14与函数y=x2+bx+c表示同一个函数，则b=-8，c=14.

总结：这两种解法反映了两种不同的思维方式，解法1是直接利用条件进行正向的思维来解决的，其运算量相对较大，解法2则是利用逆向思维，将原来的问题进行等价转化，计算量减小，难度大大降低.“正难则反”是高中数学解题的一种技巧.

二、分类讨论

例2说说二次函数y=-2x2-4x+6的图像的相关性质.

（1）它有最值吗？求出它的最值.

（2）当-4≤x≤-2时，求出函数的最值.

（4）通过前面三问，你能得出什么结论？

分析：此处设计是先复习基础知识，既可以通过配方化为顶点式，说明图像的性质，也可以画出函数图像，通过图像来说性质.（1）、（2）、（3）三问分别是整个定义域、单调区间及不单调区间三种情况，让学生感受数形结合的思想，即讨论二次函数的性质，常常要借助于图像来进行研究.而第四问，则是对上述结论作个总结.让学生再次感受分类讨论思想和数形结合思想，而这正是高中数学最常用的两种思想.

解：（1）y=-2x2-4x+6=-2（x2+2x）+6=-2（x+1）2+8.

由-2＜0，得函数有最大值8.

（2）当-4≤x≤-2时，函数的图像为对称轴左边的一段（如图1），通过图像可以发现，函数值是随着自变量的增大而增大的（即是单调递增的）.

当x=-4时，y有最小值-10；当x=-2时，y有最大值6.

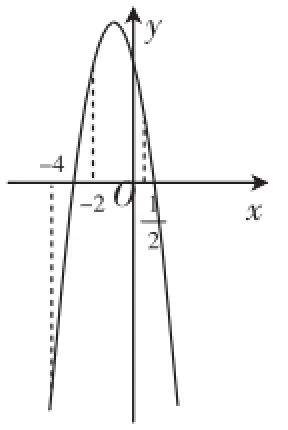
图1

延伸：已知（-5，y1）、（-4，y2）、（-1-，y3）、（-1，y4）、（-1+，y5）、（3，y6）是函数图像上的六点，试比较y1、y2、y3、y4、y5、y6的大小（.用“＜”连接）

例3已知函数y=x2，-2≤x≤a，其中a＞-2，求该函数的最大值与最小值，并求出函数取最大值和最小值时所对应的自变量x的值.

分析：根据函数图像的最高点确定最大值，根据最低点确定最小值，根据最高点、最低点以及连续状况确定y的范围.本例中函数自变量的范围是一个变化的范围，图像就是一个变化的曲线，我们需要对a的取值进行讨论，来确定函数图像的最高点与最低点.

解：（1）当-2＜a＜0时，由图2可知：当x=-2时，函数取得最大值4；当x=a时，函数取得最小值a2.

（2）当0≤a＜2时，由图3可知：当x=-2时，函数取得最大值4；当x=0时，函数取得最小值0.

（3）当a≥2时，由图4可知：当x=a时，函数取得最大值a2；当x=0时，函数取得最小值0.

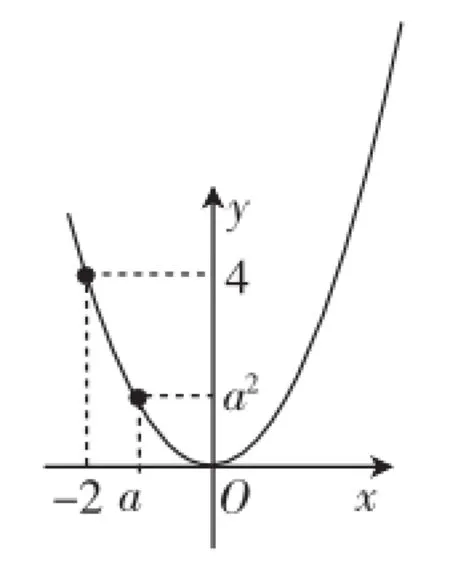
图2

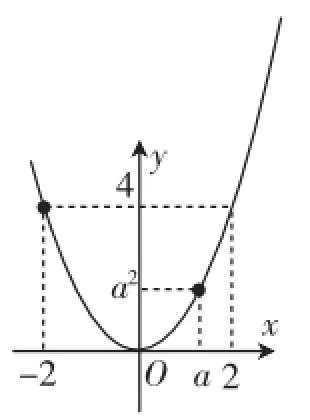
图3

图4

变式：已知函数y=4x2-4ax+a2-2a+2，当0≤x≤2时，函数取得最小值3，求a的值.

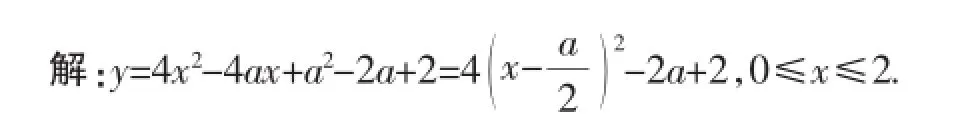
总结：高中阶段对于二次函数的研究，自变量的取值往往都不是取遍所有的实数，而是在部分实数范围内来研究.在本例中，利用了分类讨论的思想，对a的所有可能情形进行讨论.在解决这一类问题时，通常需要借助于函数图像来直观地解决问题.以开口向上的二次函数为例，根据对称轴与x的范围之间的关系来划分，区间上的二次函数图像有四种情况，如图5.

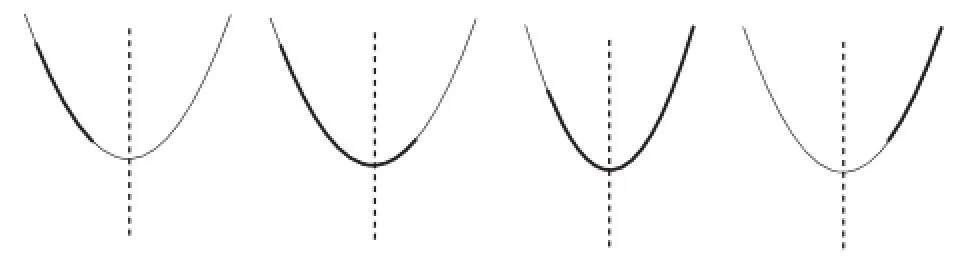
图5

总之，二次函数在初、高中的数学教学中，具有重要地位，只有做好衔接工作，才能使学生的函数学习顺畅，才能更好地进行后续的学习.