突破外形干扰建构适用模型——由一道考题的分析说起

☉江苏省如皋市石庄镇初级中学 孙来扣

突破外形干扰建构适用模型
——由一道考题的分析说起

☉江苏省如皋市石庄镇初级中学 孙来扣

数学模型，生成于学生的数学认知活动之中，是学生化解新的数学问题的重要工具.在初中阶段，很多数学问题的解决都需要借助已有的数学模型，如相似问题中的“K形图”、二次函数的几种常用解析式等.这些数学模型是学生的数学认知活动的规律总结，在一定范围内具有普遍性和适用性.因此，在教学中，一线老师对模型教学十分关注，他们努力将模型建构在学生获得“四基”的过程之中，让学生不断经历用已有数学模型解决新的数学问题的过程.然而，在模型应用过程中，很多学生记住了数学模型的外表——“形”，而忽视了模型的内核——“型”（即“内在的知识结构”），在很多新的问题的化解中选择了一些看似适用却不能用的模型，导致无法求解.近期的模拟考试中，就遇到了这样一道题，其解答状况令人担忧.现结合这道试题的考情分析，谈谈笔者对模型教学的思考，希望对您有帮助.

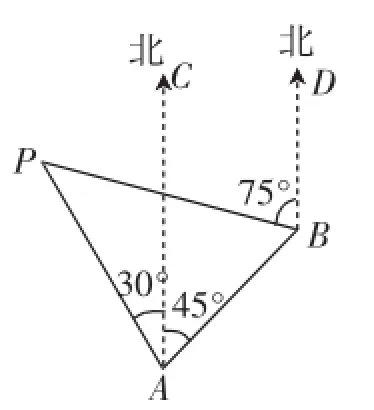
图1

一、原题简析

原题如图1，一货轮在A处，测得灯塔P在货轮的北偏西30°的方向上，随后货轮以30海里/小时的速度沿北偏东45°的方向航行，40分钟后到达B处，此时测得灯塔P在货轮的北偏西75°的方向上.求此时货轮距离灯塔P的距离PB（结果保留根号）.

简析：这是一道锐角三角函数的应用题，主要考查方位角、解直角三角形、锐角三角函数的定义、等腰三角形的性质和勾股定理等知识.根据学生的现有认识水平，原图中的具有公共边的两个三角形在解答本题时并不适用，需要打破原来的三角形的分割方法，重新建构“具有公共边的两个直角三角形”.因此，找出建构有效的数学模型的有效途径，是学生化解本题的关键.

正解：如图2，过点A作AE⊥PB于点E.

根据“30海里/小时”和“40分钟后到达”，可得AB= 20海里.

由AC∥BD，可得∠DBA=180°-∠CAB=135°.显然，∠PBA=60°.

图2

在Rt△APE中，∠EAP=∠EPA= 45°，根据“等腰三角形的性质”，易得PE=AE=10海里.

图3

二、考情分析

考情简述：在这次测试中，能完整给出“正解”过程的同学并不多.试卷批阅结束后，笔者对学生的解答状况进行了详细分析，并与部分解答出错的同学进行了交流.通过分析与交流，发现绝大多数出错的同学是“设AC与PB相交于点G”（如图3），然后想利用图中的△PAG和△BAG来解决问题.但由于这两个三角形不是直角三角形，他们求解时发现锐角三角函数并不能发挥作用.于是，他们“分别作出了△PAG和△BAG的边AG上的高PE和BF”，构造出了一个含有30°和一个含有45°的直角三角形.看似熟悉的直角三角形，却让他们的求解陷入了“困境”，围绕这样两个三角形做了很多“文章”，但最终都无功而返.显然，围绕原图作出的这些分析并没有给这道问题的解答“敞开大门”，反而让接下来的求解之路越走越窄，最终得不到正确的答案也就无法避免了.

原因分析：在锐角三角函数的教学中，学生已经建构了一些解题模型.如图4，这是“有一条公共边的两个叠合的直角三角形”模型；如图5，这是“有一条公共边的两个叠合的直角三角形”模型.图5中，AD为△ABC的边BC上的高，恰好是Rt△ABD和Rt△ACD的公共边，通过AD可以将两个直角三角形关联起来.上面的试题出现“大面积”无解，正是这一模型的“误导”.出错学生均误认为图1中△PAB是图5中的△ABC绕点A进行的旋转，AD恰好旋转到了图1中的竖直位置上的AC处.看似没有关联的图形，经过学生脑海中的一转，配上了图1中数据30°与45°被AC的“准确”分割，学生不重新分割三角形，直接顺着AC求解也就不足为奇了.

图4

图5

三、模型教学的几点思考

从上面的分析我们不难发现，学生在应用解题模型化解数学问题时，主要关注的还是“形”，只注重模型的外表，而忽略了模型的内在知识关联，让模型的应用仅停留在“临摹”的层次上.要想学生在问题解决的过程中突破模型的外形迷惑，我们可以从以下几个方面做些努力.

1.模型教学立足“四基”，强化关联

“数学模型，运用符号或数学公式，予以模拟表示”，它生成于学生的数学认知活动中，是学生经历探究活动归纳总结出的用以化解数学问题的工具，具有较强的延续性和适用性.在初中阶段，数学模型比较简单，综合程度不高.很多数学模型是由一个或几个数学知识整合而成，提取与应用这些模型所涉及的知识与技能并不复杂，这些模型主要指向简单的数学问题或实际问题.基于上述特点，在初中阶段，我们应将模型教学蕴含在学生获得基础知识、基本技能、基本数学思想及基本活动经验的过程之中，让模型建构在“四基”之上，以知识获得为起点，以模型生成为中间目标，以坚实的认知基础成就有效的数学模型.由于初中阶段的数学模型是基础模型，为了凸显出数学模型在问题解决中的作用，我们应将这些基础模型进行有效关联，将关联较大的数学模型链接成串，形成有效的“模型链”.在学生解决问题时，提取和应用数学模型也就会出现“牵一发而动全身”的“链接效应”.以垂径定理为例，我们由圆的轴对称性获得了垂径定理，产生了“垂径定理直角三角形”，此时可以链接上“勾股定理”模型，在勾股定理模型之上，再链接上方程模型，这样就形成了一个以“勾股定理”模型为桥梁的“模型链”.提取这一模型解题，学生自然会思前想后，在模型的选择和应用上敞开思路，得到正解.再以上面的试题为例，图4是“有公共边的两个直角三角形”模型，我们可以将其与勾股定理、方程、常用三角函数关联，形成一个“模型链”.这样一来，化解此题自然就有多条路径了，自然就不会出现“只读图形，而忽略了文字、符号之间的联系”的情形了.显见，数学模型链的生成，能让学生从多个角度思考数学问题，能帮助学生有效突破一些外在表象的迷惑，为学生获得有效的解题途径提供了多种可能.

2.模型建构反复尝试，力求适用

反复尝试，是数学模型建构的必经之路.任何数学问题或生活问题的解决，都不是一蹴而就的.理清问题的情境需要反复尝试，一字、一词、一句、一符、一图都需要学生反复揣摩，方能捕捉到有用的问题解决的信息；明晰问题的指向和解题所需知识的需求反复尝试，问题解决必须先摸清问题的来路，当我们能顺着问题的“来路”继续走下去，才会让解题变得顺畅；分析解题思路和解题方法需要反复尝试，走得通，再走走，走不通，回头再来，实在不行，换个角度再看看，问题解决本应如此；形成解题模型还是要反复尝试，初中阶段的数学问题和实际问题有一定的综合性，还是需要模型组合的，加之数学模型隐藏在学生的认知网络中，并不会随时随地出现，因此，必要的反复尝试将会让学生找到最佳的解题模型，让他们在适用的基础上“定下心来，就这么做了”.图3是学生选择的适用于解决“原题”的有效模型，然而思维定势让他们没能继续沿着这一模型走下去，造成这一结果的原因是多方面的.对原图的盲从，让他们的思维始终定格在模型的“外形”上，从问题分析开始，“熟悉感”让他们走上了一条“无法求解”的道路；在问题解决时，反复在同一条路上尝试，让他们心生烦躁，懊恼自不必说，甚至开始怀疑老师与自己共同努力建构的数学模型有“问题”.应该说，学生产生这样的想法并不意外，在测试后就有学生表达了自己的想法，笔者通过一个手势进行了指点，学生立即明白了，并大为感叹：我怎么没敢这么想呢？早知道我也试一下了.看来，还是尝试的力度不够，在教学中，应鼓励学生反复尝试，只有不断试误，才能发现问题解决的最佳路径，才能获得最适用的问题解决的数学模型.

3.模型应用关注本质，及时抽象

对初中阶段的学生来说，能够想到用数学模型去解决新的数学问题，是一件不简单的事情.当学生出现这样的解题行为时，我们应予以鼓励并加以引导，让他们经历“抽象问题情境，建构解题模型”的过程，让他们充分感知数学模型与“四基”间的联系，学会从本质上应用模型.细细分析试题的解答状况，慢慢解读学生的求解历程，一个问题自然而然就呈现在眼前：为什么想不到图2中的辅助线AE呢？“设AC与PB相交于点G”看似应用了图3这一模型，实则是没能理清图3的真正内涵，关注外在的“形”，而忽略了内在的“神”.图3是“有公共边的两个直角三角形”模型，公共边是模型的一个条件，两个三角形也是一个重要条件，这些都是学生的关注点，出错的学生对此关注尤为到位.要注意的是，这个模型中的一个更为重要的条件是“直角三角形”，如果将这个条件忽略了，接下来的求解自然就会缺少“直角三角形”的支撑.在现阶段，直接利用图1求三角形中的边和线，显然是十分困难的.所以很多学生无法给出正确的解题过程也就在意料之中了.这就告诉我们，在今后解决数学问题或实际问题时，应关注问题与数学模型的本质之间的内在关联，将问题情境中的条件与数学模型的核心条件认真比对，确保从问题情境中抽象出的解题模型与已有的数学模型高度相似.当两者之间有明显差别时，我们应对解题模型进行必要的调整，一方面，再回问题情境重建解题模型，直到完全匹配才能结束探究.另外，我们也可以适度修正解题模型，通过添加辅助条件等方式实现模型间的匹配.总之，解题模型的建构应以适用为终极目标.

四、结束语

数学模型与学生的数学探究活动息息相关，它们在新知探究过程中生成，在解题训练中得到巩固与提升.在问题解决过程中，能不能建构出有效的数学模型非常重要.毋庸置疑，模型“外形”特征对学生提取与应用合适的模型解题干扰很大.为此，新知教学中，我们应为模型建构准备充足条件，储备模型生成必需的基础知识和基本技能；复习巩固时，应突出模型间的关联与融合，形成有效的模型链，让模型应用“牵一发而动全身”；解题训练时，我们设置不同变式模型应用训练，不断强化学生对核心模型的应用体验……总之，数学模型的应用不应为外形所干扰.能想到用模型解题是一种进步，能选择适用的数学模型说明学生的数学思维又向前迈出了一步，而真正说明学生数学思维卓有成效的是用适用的模型化解新的数学问题.在这条路上，我们还要做很多事，比如找到模型教学的最佳时点，找到不同模型之间的衔接点等.期待您能参与到模型教学的研究中来，同时，也恳请您能对本文中的不足提出宝贵的意见和建议.

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2.高俊元.一组旨在改变学生学习方式的中考题［J］.中学数学杂志（初中版），2006（1）.

3.丁银杰.“锐角三角函数”课本习题拓展探究［J］.初中生世界（九年级），2014（2）.

4.印冬建.突出核心主线追求有效教学——谈初中数学有效备课的做法与思考［J］.中学数学（下），2014（1）.