从“学不得法”谈从条件寻找思维起点
——以一道试题的一题多解为例
☉江苏省海门市货隆初级中学 陈宏亮
从“学不得法”谈从条件寻找思维起点
——以一道试题的一题多解为例
☉江苏省海门市货隆初级中学 陈宏亮
笔者任教的农村初中有部分学生平时学习很努力,学习习惯也很好,练习时准确率也很高,但是到考试时就是不尽如人意.这部分学生学习表现为记忆力较好,擅长文科,其学习特征是机械、呆板,理解慢,知识点总是死记硬背.因此他们基础非常扎实,但遇到综合性的题目就无从下手.我们总是评价他们“学不得法”,其实,这是学生思维能力欠缺的一种表现.“课程标准”指出,数学课程内容要反映社会的需要、数学的特点,要符合学生的认知规律,它不仅包括数学的结果,也包括数学结果的形成过程.同时要求教师教学时应该以学生的认知发展水平和已有的经验为基础.这一要求就决定了教师的教学应该注重发展学生的思维能力.本文笔者尝试在课堂教学中利用综合题的条件分析逐渐培养学生从条件寻找思维起点的能力,进而提高学生的思维能力.
一、例题教学过程
1.教学背景
例题是笔者所在学校初三中考一模的第27题,此题是纯几何证明(计算)题,分值为12分,班级平均得分只有1.3分,高分也只有6分.考试结束后通过与学生的交流以及对题目进行分析,发现知识点运用灵活性较大,学生的思维障碍在于做第一问时无法准确添加辅助线,而部分同学进行“尝试性”添辅助线,尝试很多次也无法解决,时间花了很多,但是效果不佳,因此笔者决定把例题的第一问作为突破口,引导学生从不同条件中寻找问题解决的思维切入点,达到一题多解的效果,训练学生这方面的能力.
2.例题展示
在△ABC中,AC=BC,∠ACB=120°,点D在AB边上,∠EDF=60°.
(1)当点D为AB的中点且∠EDF的两边分别交线段AC、BC于点E、F时,如图1,求证:DE=DF.
(2)当点D不是AB的中点,且AD∶AB=1∶3时,
①若∠EDF的两边分别交线段AC、BC于点E、F,如图2,求DE∶DF;
②若∠EDF的边DE交线段AC于点E、边DF交BC的延长线于点F,如图3,直接写出DE∶DF的值.
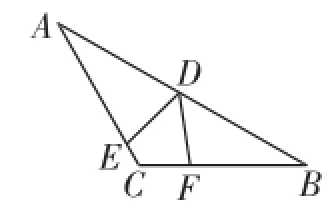
图1

图2

图3
3.例题分析
几何证明(计算)是根据一定的规则或标准,由公理和定理推导出某些命题的过程.其过程分为分析、证明、整理三个过程.分析:分析图形的切入点及所证(求).证明:作出辅助线,综合运用定理、模型等方法,找出已知和未知的联系,或推翻否定命题不成立的假设.整理:规范作答.分析过程是问题解决的重中之重,因此思维的切入点的选择至关重要,思维起点有很多种,例如:从问题目标的特征选择;从问题结论和解法选择;从观察和实验中寻找等.而问题条件构成了问题分析的背景,通过对背景的分析还原出问题的初始形态,因此问题的条件分析是一个重要的思维起点,从这一入口进入问题的证明(计算)过程,最终得出相关结论,到达思维的终点.
问题(1)的分析如下所示.
思维起点1:在△ABC中,AC=BC,∠ACB=120°以及D为AB的中点.
分析过程:由已知条件得到∠A=∠B=30°,引导学生考虑到三角函数,但是本题中没有直角三角形,因此需要构造,如何构造?观察结论要证得DE=DF,需要相等


