追求逻辑连贯的数学教学——以“多边形内角和”教学为例

☉江苏省徐州高级中学 刘 华

追求逻辑连贯的数学教学
——以“多边形内角和”教学为例

☉江苏省徐州高级中学 刘 华

我们知道，初中平面几何内容主要来源于《几何原本》，前后知识的逻辑连贯是其特色.笔者最近观摩了一次同课异构教学活动，开课课题是“多边形内角和”，本文记录两种不同风格的教学设计，并给出解读和反思，与同行研讨.

一、两种教学设计

（一）第一种教学设计

教学环节1：创设情境，引入新课.

问题1：某个多边形所有的角加起来等于它的外角和，那么该多边形是几边形？小明仅用几分钟就解决了问题，你能吗？

问题2：用四块大小、形状完全相同的四边形可拼成一块无空隙的纸板，你知道为什么吗？

设计意图：这样一开始设疑，学生很容易发问，这个多边形是几边形呢？用四块大小、形状完全相同的四边形可拼成一块无空隙的纸板，为什么会产生这种效果呢？从而可调动学生的学习兴趣和注意力，创设恰当的教学情境.

教学环节2：合作交流，探索新知.

（1）问题：三角形的内角和等于多少度？外角和等于多少度？长方形的内角和等于多少度？正方形的内角和等于多少度？

（2）问题：任意四边形的内角和等于多少度呢？你是怎样得到的？你有几种方法？

（3）学生思考并分组讨论，教师深入小组参与活动，指导倾听学生交流.

（4）学生分组选代表展示小组的探索成果，师生共同进行评判，对学生找到的不同的方法及时给予肯定.

设计意图：学生可能找到以下几种方法：“量”——先测量四边形四个内角的度数，然后求四个内角的和；“拼”——把四边形的四个内角剪下来，然后拼在一起形成一个周角；“分”——通过添加辅助线的方法，把四边形割成三角形.

教师在学生展示完后提问：在“量”“拼”“分”这几种方法中，哪种方法简单又相对准确？我们刚才找到了几种作辅助线的方法，它们的共同点是什么？

教学环节3：自主探究，得出结论.

（1）问题：用刚才类似的方法，你能算出五边形、六边形、七边形的内角和吗？

（2）问题：依次类推，n边形的内角和等于多少度呢？

设计意图：让学生自己归纳总结，得出n边形内角和公式为（n-2）·180.

教学环节4：应用新知，尝试练习.

（1）想一想：如果一个四边形的对角互补，那么另一组对角有什么关系？为什么？

（2）算一算：四边形、五边形、六边形以及n边形的外角和呢？

教学环节5：归纳总结，形成体系.

从以下几方面引导学生进行小结.

（1）现在你能解决情境中的两个问题吗？

（2）这节课你学习了哪些知识和方法？你有什么收获？

（二）第二种教学设计

教学环节1：回顾旧知，猜想新知.

提问：回顾三角形的内角和和外角和，猜想多边形的内角和与外角和.

预设与引导：三角形的内角和等于180°，外角和等于360°.如图1，可以通过作平行线，平移∠1、∠2、∠3到三角形的一个顶点处，得到一个周角，说明∠1＋∠2＋∠3＝360°.例如过点C作CD∥AB.

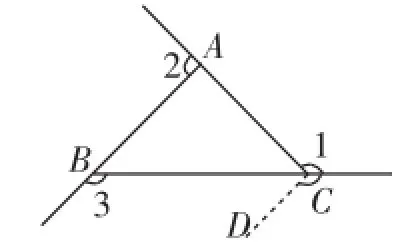
图1

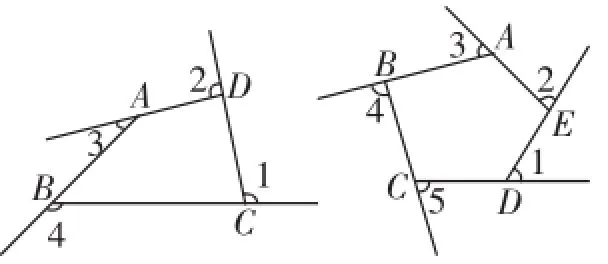
图2

当边数增加时（如图2），多边形的内角个数、外角个数随之增加，多边形的内角和和外角和会随之发生变化吗？

（同学们自己思考、探究、猜想、伴以小组讨论）

教学环节2：全班交流研究的方法和成果.

（1）先研究内角和，后研究外角和.

以四边形为例.

怎样研究？——作辅助线，将原多边形分成若干个三角形（如图3）.

图3

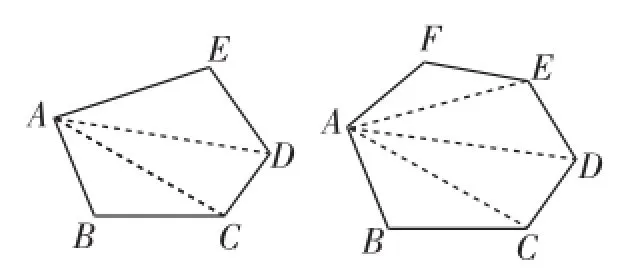
图4

方法1：过四边形ABCD的一个顶点作对角线，再由四边形扩展到n边形（如图4）.归纳出：

过一个顶点所作的对角线条数等于（n-3）；

过一个顶点作对角线，将原n边形分成的三角形的个数为（n-2）.

n边形的内角和等于（n-2）·180°.

方法2：在多边形的边上、形内或形外任取一点O（如图5），与各顶点连接，运用“三角形内角和等于180°”同样可得上述结论.

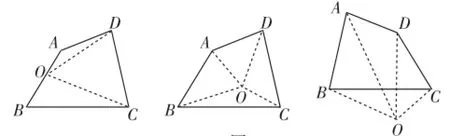
图5

由多边形内角和公式和多边形外角定义，易得：多边形的外角和等于360°.

（2）先研究外角和，后研究内角和.

如图6，过C作CE∥DA，CF∥AB.则∠DCE＝∠2，∠ECF＝∠3，∠FCM＝∠4.

由周角定义可得：∠1＋∠2＋∠3＋∠4＝360°.

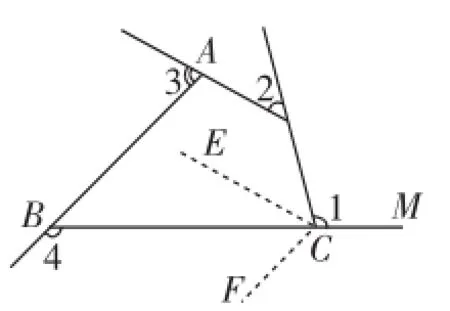
图6

即：n边形的外角和等于360°.

根据多边形外角定义及“多边形的外角和等于360°”，易得多边形的内角和公式：多边形的内角和等于（n-2）·180°.

师生总结：

当多边形的边数变化时，多边形的内角和随之变化，为变量，而外角和却始终不变，为一个常量360°；

在研究变化过程中的数量关系时，可从变量入手，也可从不变的量入手研究；

教学环节3：练习巩固.

练习1：（改编自教材习题）如图7，五边形ABCDE中，必须已知怎样的条件方可求得∠E的度数？

预设意图：学生自己思考编题、解题.教师预设如下.

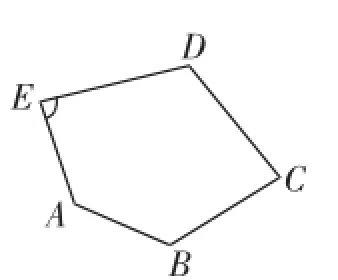
图7

（1）已知其他4个角的度数（∠A＝135°，∠B＝120°，∠C＝60°，∠D＝150°）；

（2）已知与∠E相邻的外角的度数或它们之间的数量关系.

练习2：一个多边形的各内角都等于120°，它是几边形？

变式：根据多边形的外角与相邻内角的互补关系，正多边形的各个内角相等，外角也相等.还可编出哪些求边数的问题？

如：一个正多边形的内角和等于外角和的4倍，求边数；

一个多边形的内角和比它的外角和的5倍少180°，求边数.

教学环节4：小结.（略）

二、解读和反思

1.第一种设计的主要立意

首先是教材处理上较有特色，比如将教材中的例题改编成练习，由学生自己尝试解答；将教材中求六边形的外角和，改为练习中的“算一算”，先让学生求四边形的外角和，再探索五边形、六边形及n边形的外角和.这样处理主要是体现学生的自主性，使学生变“被动”为“主动”.教学形式上，将不少练习采取分组竞赛的形式合作完成，使学生产生强烈的学习兴趣，追求较好的课堂气氛.

2.第二种设计的主要立意

开课阶段，教者首先从学生实际出发，引导学生回顾三角形内、外角和定理及其证明方法，在教师设置的问题引领下，使学生选择适当的研究策略，使学生认识到只要类比三角形的内角和定理及外角和的证明方法，通过添加辅助线，将其转化为三角形就可以解决新问题.这样做不仅让学生再次体会类比和扩展方法的使用，以及把复杂问题化为简单问题，化未知为已知的思维方法，而且使学生体验到事物的“对立和统一”“矛盾与转化”的规律.

3.两种教学设计的对比

可以发现，第一种设计只是对教材的亦步亦趋、小修小改，属于尊重教材、严守教材的一种教学取向，课堂容量有限，表面上学生活动形式多样、课堂气氛活跃、有大量展示，但是数学的思维活动却不能与第二种教学设计相比.在第二种教学设计的课堂上，我们注意到课中教者巧妙地把同类的问题放在一起让学生去感受、去体会、去总结；引导学生从问题个性中探求共性，寻求变异，多角度、多层次去构思、延伸、拓展，这样引导学生自主探究，有利于激活学生的思维，使学生的学力得到有效锻炼和提高，是一节更有数学味儿的课堂，也是我们应该追求的前后一致、逻辑连贯的数学教学取向.

1.李庾南.自学·议论·引导教学论［M］.北京：人民教育出版社，2013.

2.章建跃，陈向兰.数学教育之取势明道优术［J］.数学通报，2014（10）.

3.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

4.【日】佐滕学.21世纪学校改革的方向［J］.人民教育，2014（1）.

5.马立平，著.小学数学的掌握和教学［M］.李士锜，吴颖康，等，译.上海：华东师范大学出版社，2011.