基于教材研究的教学设计“六要点”*

☉江南大学附属实验中学 庞彦福

☉江苏省锡山高级中学实验学校韩诗贵

·江苏省无锡市庞彦福名师工作室·

基于教材研究的教学设计“六要点”*

☉江南大学附属实验中学 庞彦福

☉江苏省锡山高级中学实验学校韩诗贵

笔者拙文《数学教师的“六研究”》（发表于《中学数学》（初中版）2014年第3期，人大《复印报刊资料·初中数学教与学》2014年第6期全文转载），其中一个“研究”就是“研究教材”.

《辞海》中解释：“教材是根据教学大纲为师生教学应用而编选的材料，主要有教科书、讲义、讲授提纲等.有时也包括供教师和学生用的教学参考书、教学辅导材料等.”当然，现在教材编写是根据课程标准.其实，能够对人有教育作用的材料也算教材.教材最主要的是包括学生学习用的“教科书”和教师教学用的“教师用书”.教科书是课程标准的具体化，是一个课程的核心教学材料.教科书作为社会主流文化和价值观的重要载体，遵从的是国家课程标准的思想精神，体现的是时代发展对人才培养的要求.教科书是国家教育意志的体现，是教师进行教学的主要依据，它为教师备课、上课、布置作业、学生学习成绩评定提供了基本材料.

教师研究教材不能浮于表面，应该是系统性的、深层次的学习与理解.只有深入研究教材才会有真正的课堂教学.从某种意义上讲，教师对教材的理解深度决定了其教学高度.对教材理解不透，或不理解教材的安排体系、教材内容的逻辑关系，那就只能是教教材，用教材教就会变成一句空话.课程改革向纵深发展，但“真正决定数学课程的不是写在书上的各种观念与规定，而是天天和学生接触的教师”.尽管专家们花了大量的精力，认真修改了课标和教材，但是，课堂上、教学中，数学教师便决定了一切.所以，实施有效教学，则须深入学习和研究教材.

一、教学内容

教学中我们常常会思考教什么、怎样教、为什么这样教的问题.其实，这就是研究要教学的内容，以及对教学内容的解析.对教学内容的研究不是单纯地、独立地研究本节课的内容，而是要站在系统的高度上整体地理解本节课内容在章节、版块中的建构与作用，研究知识的来龙去脉，研究知识的系统结构，这样才会了解并理解教学内容的地位、作用及其用途.譬如“零指数幂与负指数幂”的教学，不能只要求学生死记硬背两个规定：不为零的数的零指数幂等于1，不为零的数的负指数幂等于这个数的正指数幂的倒数，而是要真正理解这两个规定的合理性及其来龙去脉才是根本，只有弄清楚零指数幂与负指数幂是从哪里来的，才能会计算它们、运用它们.研究教学内容才能是真正吃透教材，才能够准确把握教学的重点，理清教学内容、各知识点之间的关联性，内含于其中的基本思想与逻辑关系，找准教学的起点、基础及核心思想，从而实现有效教学.

二、教学目标

目标是所期望的成果.教师通过一节课或一个单元的教学，我们期望取得什么样的成果，这就是教师的教学目标，也应该是学生学习的目标.无论是学科教学的目标，还是章节的教学目标，落实到课堂上往往都要细化为课时目标.教学目标是课堂教学发展的方向和要达到的目的，它为教学内容、教学方法、教学的组织行为、教学评价方式的选择提供了依据.教师在设定教学目标之前要明白为什么这样设置，设定教学目标的依据是什么，如何在学生层面上落实教学目标.我们不妨通过图示（图1）来理解教学目标的设定.

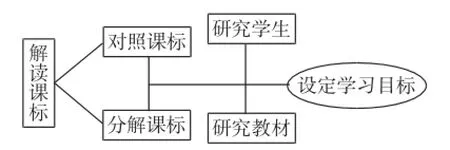
图1

教学目标的设定要基于课程标准，要忠实于教学内容.“对照课标”是指对照《课标（2011年版）》与《课标（实验版）》.和数学课程目标一样，教学目标也包括结果目标和过程目标.结果目标是要了解、理解、掌握和运用，而过程目标则需要经历、体验和探索等途径才能实现.设定教学目标还要考虑学生的认知基础及实际情况，如果教学目标不能在学生身上得到落实，设定的目标就可能成为一种“摆设”.教学目标明确教学设计才能有效，教学活动才会有针对性.设定教学目标要本着“学生学完这些之后能够做什么”，教学目标是数学活动的结果，更是数学教学设计的起点.

三、教学问题诊断

教学中的问题来自于学生的学习过程，学生的认知障碍、学习难点、容易出错的地方是教师实施教学之前就应该研究和重点把握的对象.对教学问题的诊断和把握，对于有一定教学经历的教师来说往往是来自教学经验，那么，对于新教师而言该怎么办呢？其实，除了经验之外，更是对教材的研究与理解，这当然离不开对课标的了解和熟悉.真正走入教材、挖掘教材、理解教材之后，我们就会发现越来越多的问题，这不仅是教学的资源，更是对教学问题的诊断与把握.当教师对教学问题诊断不准确的时候，教学效果往往是不理想的，对学生的评价也会出现偏颇.比如在基础一般化的班级里上完“零指数幂与负指数幂”之后，进行课堂检测，其中有以下两个题目：“（1）已知（x-1）x+2=1，则整数x的值为_________；（2）求使得（x-2）x2-4=1成立的x的值.”结果很少有同学全对，这就是对教学问题没有正确诊断导致的结果.本节课中，学生能否将“非零数的零次幂等于1，1的任何次幂都等于1，-1的偶次幂等于1”融为一体，从（1）到（2）学生又能否从三种情况中查找出不符合条件者，体现的不仅是思维的发散性，更需要思维的批判性.教学中要探寻学生错误的背后是什么？如何研究并解决这些错误.

四、教学资源利用

教学资源不仅有教材本身，还包括丰富的补充读物，例如工具书、挂图、图表和其他教学辅助用具，教学程序软件包，例如幻灯片、电影片、音像、光盘、磁盘等.教学资源的开发与利用要依据学校教学的自身条件、教学内容及学生实际情况来选择和确定.PPT课件、word文档、多媒体的展台、微课、翻转课堂的材料利用及自制教具等，都可以成为课堂教学的有效资源.教学资源是为课堂教学服务的，是为学生学习服务，不能偏离了教学的主题，要体现教学内容的本质，要彰显数学教学的内涵.

五、教学过程设计

作为一个系统性活动的教学设计，是教师对将要进行的课堂教学勾画的愿景.教学设计过程应该是主题明确、结构清晰、脉络分明、活动安排有序，它是教师对将要实施的课堂教学的认识和期望.教学设计过程是对课堂行为的一种事先筹划，是对学生达成教学目标、体现学业进步和情境及活动做出的精心安排，所设计的情境应该是学生理性思维的生长点.数学教学设计的根本目的就是帮助学生进行有效的学习数学，数学课堂教学设计过程在很大程度上决定了数学活动的效果.教学设计是一种有目的任务分析，即假定有一个任务要完成（目标），如何才知道做好了（评价），我们该怎么做才能完成这个任务（活动）.目标前面已经说过，因此，活动则是教学设计的重要因素.基于实践，有效的教学设计应该是在明确学习目标和确定实施学习目标的评价方式之后而设想实现目标的教学活动.所设计的教学活动要富有主体性、情境性、合作性及针对性，让活动有任务的引领，这样就有了开展活动的支撑点与着落点，通过活动任务，学生可以理解学习的意义，形成自己的知识结构.

教学设计的核心是为实现一定的学习目标，面对具体的学生，必须“寻找”到最贴近学生学习生活实际的、最能启迪学生心智的活动设计，如此才能真正体现学生的主体性，才是最成功的教学设计.教学设计可以是“讲解—传授”式，可以是“引导—发现”式，可以是“活动—参与”式，也可以是“自学辅导”式.有效的教学活动是学生学与教师教的统一，学生是学习的主体，教师是学习的组织者、引导者与合作者.所设计的数学活动要站在学生的角度，从学生的问题出发，要让学生经历活动，通过学生自主、合作、探究等方式，达到学习过程的自我建构，促进学生思维发展.笔者对“苏科版初中数学”的“多项式的因式分解（第1课时）”的设计流程是：（1）学生先学，寻找教学起点；（2）自主学习，发现理解；（3）暴露思维，合作解疑；（4）沉淀思维，积累经验；（5）深化理解，拓展运用；（6）梳理小结，提炼升华；（7）课后延伸，感悟应用.浙江名师潘小梅老师在“神通广大的平行线：等积变形”一课的教学中是这样设计的：（1）复习引路，提出问题；（2）经历活动，建立模型；（3）由浅入深，识别模型；（4）拓展训练，运用模型；（5）欣赏数学，感悟应用；（6）梳理小结，提升思想.

六、选题与检测

数学教学离不开题目，离不开解题.课堂教学中的每一个例题、练习都应该是认真研究之后精选的，课堂检测题及布置给学生的作业也应该是精心选取的，这样，教学才会具有针对性，检测才会促进目标的达成，课后作业才能起到巩固、理解、深化的作用和效果.课堂上的例题、练习的选用要紧扣学习内容，贴近学生实际，让学生跳一跳够得到，又不失对思维的培养.检测要让绝大多数的学生过关，以树立学生学习的信心，并且要有适当的易出错题和思维爬坡题，留给学生思考和发展的空间.课后作业是为了将课堂探究向外延伸，起到巩固知识、理解运用、深化探索、拓展延伸的目的，布置的作业应该分层，否则，基础薄弱的学生就无法完成，课后作业就会成为无效操作或“抄作”.苏科版八年级（上）“等腰三角形的轴对称性”一节中在定理“直角三角形斜边上的中线等于斜边的一半”之后给出了“如图2，如果∠A＝30°，那么BC与AB有怎样的数量关系？试证明你的结论.”显然，课本的意图是让学生探究来完成的.一位老师布置作业时针对学有余力的同学安排了一道选做题“已知在△ABC中，∠B＝30°，AB＝6，AC＝5，求△ABC的面积.”这样的因材施教不仅是对本节课内容的深化，更有助于学生进一步对全等三角形中“SSA”的理解.“用教材教而不是教教材”，不是口号而是教学的理念和做法.对教育教学的评价要有助于学生“提高发现问题和提出问题的能力、分析问题和解决问题的能力”，有利于学生的进一步学习、成长和发展.

如果说哲学试图用有限的语言表述无穷的宇宙的话，那么数学试图用有限的语言表述无穷的哲理，或者说数学试图用简洁的语言表述丰富的内涵.因此，数学教学离不开研究.

图2

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2.夏征农.辞海（1989年版）［M］.上海：上海辞书出版社，1990.

3.马小为，庞彦福.初中数学有效教学模式［M］.北京：北京师范大学出版社，2014.

4.庞彦福，詹慧，翁寿峰.数学教师的“六研究”［J］.中学数学（下），2014（3）.

5.潘小梅.以活动促进思考，在感悟中提炼经验［J］.中学数学教学参考（中），2014（3）.

6.庞彦福.着力问题意识促进思维发展［J］.中学数学教学参考（中），2014（3）.

7.钟珍玖，庞彦福.“数学理解”内涵及教学价值探微［J］.中学数学（下），2014（3）.H

*本文为江苏省无锡市教育科学研究教师教研专项课题《初中数学课堂中的数学美教学实践研究》（立项批准号为：2014WXJYD1）的阶段性成果.