“微话题”探讨,促进教与学的和谐发展
——以“邻补角与对顶角”为例
“微话题”探讨,促进教与学的和谐发展
——以“邻补角与对顶角”为例
☉江苏省南通市陈桥中学 陈建均
微话题一般指小的讨论的主题.笔者在初中数学中引入微话题是对学习资源的开发和利用,围绕学习目标的达成,选择契合的微话题.微话题探讨式学习简单来说就是师生围绕微话题进行探讨,教师多听少说,在学生充分探讨的基础上,通过追问等方式参与探讨,进行相机引导,尊重学生的认知起点,强调从学生已有的知识经验和认知规律出发,引导学生再发现进行自主建构,从而促进教与学的和谐发展.本文以人教版七年级上册“邻补角与对顶角”为例谈谈如何以“微话题探讨式学习”为依托促进教与学的和谐发展.
一、听课经历
笔者有数次关于“邻补角与对顶角”的听课经历.在这里笔者梳理出两种比较典型的教学安排:部分教师认为内容简单,采取学生看书自学、交流、练习的安排进行自主学习.笔者发现这样的安排,学生的学习兴致并不高,教学效果也不理想.相当多的学生仍需要通过练习与讲解来理清“互为补角与互为邻补角”的差别及“相等的两个角是对顶角”是假命题.笔者认为究其原因还是拿来主义惹得祸,学生未曾真正经历概念与性质的归纳,学生只是一个读者;部分教师采用填空的方式和学生共同完成邻补角与对顶角的标准化概念(教材中的概念)的概括,通过练习进行概念的辨析.笔者发现这样的安排,学生学得非常轻松,短期教学效果也很好.但是优点也是最大缺点,教师的预设限定了学生的发展,编排缺少挑战性和趣味性,学生的学习能力实质上很难有多大的提高.
笔者认为上述两种教学安排本质上是相通的,跟着教材和跟着教师(导学案)学,其实还是跟着权威学.表面的和谐掩盖了学生的想法与学生之间的差异,产生的必然是标准统一、缺乏个性的产品.
对此,笔者在对听课记录进行梳理后,以“微话题探讨式学习”为依托重新进行了教学设计.且在前不久的一次课题组活动中,采用借班上课的方式进行了教学实践,得到了组内老师的热议.本文呈现该课的教学设计(限于篇幅本文不呈现教学实录),同时给出笔者的两点思考,以期得到更多同行的指导.
二、教学案例
1.教学目标
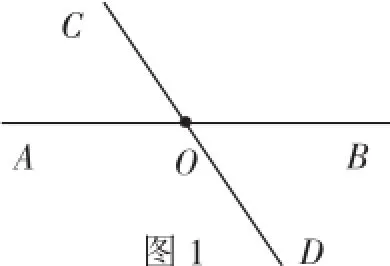
图1
(1)以观察图形、提出问题为组织先行者,引导学生自主归纳邻补角的概念和性质.
(2)类比邻补角的学习,学生自主归纳对顶角的概念和性质.
(3)在探讨交流过程中,引导学生进行提问、质疑、反思,体会数学的严谨性,感受学习数学的乐趣.
2.教学活动
活动1:聚焦学生提出的问题.
(1)如图1,如果度量出一个角的度数,想要知道其余三个角的度数还需要经过度量吗?有什么简便的方法吗?(微话题)
教学预设:在学生提出问题、分组讨论、小组汇报交流的基础上,笔者根据问题的典型性决定全班交流探讨的微话题.
在学生交流过程中,笔者追问:“为什么∠AOC+∠BOC=180°”,学生将围绕角的基本构成要素(一个顶点、两条边)和平角的概念进行解释.这个追问是本节课非常重要的一个生长点,即从所处的位置上分析两个角的关系.结合学生的叙述笔者进行板书:这两个角的顶点重合,有一条公共边,且它们的另外一条边互为反向延长线;这两个角的和是180°(这两个角互为补角).
笔者继续追问:“图中这样的角有几对?请根据上述特征给这样的两个角下个定义,起个名称.”笔者分析部分学生会出现“和是180°的两个角是邻补角”、“两直线相交,和是180°的两个角是邻补角”等极易混淆的概念.这些原生态的认识恰是最好的教学素材.笔者分析学生可以举反例解决上述问题,从而,从位置关系上给出概念成为必然之举.笔者分析学生类比互为补角给出互为邻补角的名称是比较容易的.从而,学生自主归纳出邻补角的定义“顶点重合,有一条公共边,且它们的另外一条边互为反向延长线,具有这种位置关系的两个角互为邻补角”和性质“邻补角互补”.笔者和教材的处理有所差别,分为定义和性质两部分.这样处理的理由一是顺应学生的认知方式;二是与对顶角的学习形成照应.
(2)有几对相等的角?你能加以说明吗?(微话题)
教学预设:笔者分析学生很容易发现有两对角相等,但是在理由的阐述上,要谨防学生采用特殊值法进行说明,这个非常重要,处理不好对学生后续的证明都会产生负面影响.一旦发现,笔者要追问“∠AOC=30°是成立的,29.2°、35°、110°呢?说明几个特殊值是成立的能代表所有的值都成立吗?”此处可以联系前面举反例说明错误概念的例子,进一步说明推理的科学性与严谨性,让学生意识到特殊值法进行猜想是可以的,但是不能作为证明的依据.此处注意引导学生进行规范的书写.
笔者进一步追问:“我们把图中像这样的两个角叫做对顶角,请根据你的发现给出对顶角的概念.”笔者分析仍然会有不少学生会给出“两个相等的角是对顶角”和“两直线相交,两个相等的角是对顶角”等极易混淆的概念,但是类比邻补角概念,学生应该比较容易发现存在的问题,从而自主归纳出对顶角的定义与性质.
活动2:引导学生运用所学的知识进行提问.
(1)如图1,已知∠AOC=55°,求其余三个角的度数(请尝试使用不同的方法求解).
教学预设:这个问题是笔者为引导学生进行提问而设置的引子.笔者分析绝大多数学生会依据“邻补角互补”求∠BOC和∠AOD,再依据“邻补角互补”或者“对顶角相等”求∠BOD;少数学生会想到只用“对顶角相等”求其余三个角的度数,当然需要用到周角是360°,即∠BOD=∠AOC=55°,∠BOC=∠AOD==125°.如果没有学生想到,笔者将进行追问:“如果只利用‘对顶角相等’,你能求出其余三个角的度数吗?”引导学生关注在“对顶角相等”、“这两个角的和是250°”两组等量关系下可以求出这两个角的度数(未知量的值),一是为学生后续的提问打下伏笔,二是为后续二元一次方程组的学习埋下铺垫.
(2)如图1,已知___________,求其余三个角的度数.(请添加一组条件,注意要与上题不同,即不能是已知一个角求其余三个角)(微话题)
教学预设:笔者分析学生受到上一题的启发,添加条件∠BOD+∠AOC=110°的会比较多,也会有类似∠BOC-∠AOC=70°、∠AOC∶∠BOC=11∶25等条件,解决问题的关键在于用一个角表示另外一个角(即消元思想).
(3)过点O画射线OE(OE与OA、OB、OC、OD不重合),请结合前面所学的知识(例如角平分线)设计一道计算题.(微话题)
教学预设:此处的设置在于引导学生对所学的知识进行整合,把学生引向综合题.
活动3:引导学生进行反思,开展课堂小结.
说说这堂课你的收获(包括还有什么困惑).最后请你自己和小组成员对你本节课的表现进行评价.
教学预设:笔者认为收获不能回避问题,学生需要个性化的表达,同时通过自己与小组成员的评价更能从内驱和外驱两方面帮助学生保持积极思维的状态.
三、两点思考
1.为促进教与学的和谐发展——教师需要相机引导
笔者认为进行教学前教师首先应该熟悉学情,从学生已有的知识经验出发,从数学知识的内在结构安排出发,遵循学生的认知规律,寻找恰当的切入点;教学过程中更需要时刻关注学生的思维发展,寻找鲜活的素材提炼微话题,让学生再发现、再创造,注重保持学生学习的热情,引导学生主动建构.在学生自主建构过程中因为认识上的不足等原因暴露出来的问题,教师可以采用追问等方式进行恰当的补充和引导,不要代替学生去思考、去探究.
2.为促进教与学的和谐发展——学生需要探讨碰撞
笔者认为教师多听少说是对学生最大的尊重,也是对学生成长的最大帮助,唯由让学生经过充分的探讨碰撞,学生的个性才能得到充分的释放,学生的思维障碍才会得到充分的暴露,学生的学习能力才会得到实质性的提高.本节课笔者相机引导,说得很少,就是要保障学生探讨碰撞的时间.学生的探讨碰撞极具爆发力和感染力:学生思维活跃,不断有新的想法加入;有学生发表自己的观点后,学生自发响起掌声.笔者认为学生间的竞争与协作是推动学生学习和谐发展的最好原动力.同样学生的探讨碰撞也会给教师带来新的启发,也会促进教师的发展.
四、写在最后
最后呈现的教学生成学生的表现非常出彩.正是这样的感动激励着笔者和课题组所有成员进行“微话题探讨式学习”的研究,促进教与学的和谐发展.H

