对一道旋转相似问题数学模型的探究

☉甘肃省天水市第七中学 吴俊杰

对一道旋转相似问题数学模型的探究

☉甘肃省天水市第七中学 吴俊杰

中考试题不仅对教学具有很强的指导和借鉴意义，对中考命题也有很强的启发作用.很多中考命题都是对教材习题、中考试题的变形、拓展或者直接借鉴.如何在试题教学中达到举一反三，做一题会一片（类）的效果，是每一个数学教师苦苦思索的问题，笔者认为，对有些数学问题可以增强解题分析中的数学模型意识，尝试“问题→模型→问题”的教学研究模式，是较好的途径之一.本文拟以2013年湖州市一道中考试题为例，谈谈中考复习时增强解题分析中的数学模型意识，尝试“在问题中构建模型，让模型回归问题”的教学研究模式.

一、问题展示

图1

图2

现在来证明线段B0Bn就是点B运动的路径（或轨迹）．

图3

如图3所示，当点P运动至ON上的任一点时，设其对应的点B为Bi，连接AP、ABi、B0Bi，因为AO⊥AB0，AP⊥ABi，所以∠OAP=∠B0ABi.又因为AB0=AO·tan30°，ABi=AP· tan30°，所以AB0∶AO=ABi∶AP，所以△AB0Bi∽△AOP，所以∠AB0Bi=∠AOP．又△AB0Bn∽△AON，所以∠AB0Bn=∠AOP，所以∠AB0Bi=∠AB0Bn，所以点Bi在线段B0Bn上，即线段B0Bn就是点B运动的路径（或轨迹）．

二、解后反思

（2）这是一个典型的运动问题，但却是一个陌生的运动问题，说起陌生是笔者在之前的解题学习中没有见过相关知识和类型的习题，但有一点是确定的，运动问题中通常蕴含着规律性的东西，或者某些元素保持不变性，或者某些元素变化呈现一种规律性，或者相关元素之间关系的确定性.基于这种思考，笔者大胆猜测本题也大概不出其外，如果把定角∠APB=30°，A点横坐标一般化，点B的运动路径和距离也必然与这两个结果相关.

（3）笔者再思考，既然是运动问题，笔者很自然地联想到了非常熟悉的图形变化——旋转.文1中发现了问题的本质：旋转相似，笔者从另一个角度思考这个问题：把图1在直角坐标系中整体旋转一定的角度，不会影响到B点的运动轨迹，如果旋转45°，使得直线OC与y轴重合，问题的解答会不会变得简单一些？

基于以上思考，笔者确定了以下解答思路：首先将问题一般化，建立数学模型，探索一般规律，再应用数学模型，回到原始问题，解答问题.

三、建模过程

1.数学模型的理解

模型思想是《课程标准（2011年版）》的10个核心概念中唯一一个以思想指称的概念，它是数学基本思想之一，通俗地讲，数学模型就是采用形式化的数学语言，如字母、数字、等式、不等式，以及图形、图像、图表等数学符号抽象地、概括地表征所研究对象的主要特征及其内在联系的一种数学结构表达式.在建模过程中，要把本质的东西及其关系反映进去，把非本质的、对反映客观真实程度影响不大的东西去掉.课程标准对数学模型的教学意义论述和要求的提法是“教学应结合具体的教学内容采用‘问题情境—建立模型—解释、应用于拓展’的模式展开，让学生经历知识的形成于应用过程，从而更好地理解数学知识的意义……”

个人认为，在数学解题教学中，也完全具有可能，有必要在具体的问题中抽象、概括、建立数学模型，再反过来利用数学模型指导、解答原问题，并加以应用.本文拟结合上述问题，谈谈自己在数学解题教学中通过“问题→模型→问题”的思路，尝试建立数学模型，回归问题的研究、教学态度.

2.原始问题一般化

一般化之前需要分析发现原问题中的“本质元素与核心关系”.分析问题，可以发现原问题本质元素在于“三定：定直线、定点、旋转中的两个定角（∠APB和∠PAB）”，核心关系是点P和点B之间在“旋转”中的联动关系，但是这个联动关系如何？未知.

另外，点P所在直线的函数关系式为y=-x，是否属于本质元素，再如点A为定点，问题中仅仅提到了点A的横坐标，对纵坐标一字未提，显然此处“两定”中依然有一些非本质的元素.还有∠APB=30°对这种联动关系有何影响也不明确，它们是不是本质元素？基于以上分析，在问题一般化的过程中，可以保留本质与核心关系，其他的数量元素可以字母化，即将具体数值转化为字母表示.得到以下更具有一般性的待探究问题：

设点P是定直线l上的任意一点，点A为直线外一个定点，点A到直线l的距离为a.点B在直线PA确定的一侧，且∠APB=β，BA垂直PA，当点P在直线l上运动的时候，探究点B的运动轨迹.

说明：（1）具体数字已知量的字母化：将∠APB=30°字母化为∠APB=β，因为点A为定直线l外一个定点，则点A到直线l的距离确定，表示成a，至此原问题被一般化.（2）为了问题研究的方便，也因为图1中y=-x旋转后可以到达y轴的位置，在问题研究中不妨以直线l为y轴建立直角坐标系，不妨设点A为第一象限内的一个定点.通过对图形变化过程中可能的位置分析，以及下面的分析可以发现，这一特殊处理对结论没有影响.（3）在整个运动变化过程中，虽说主动点P、从动点B的具体位置不确定，但没有必要研究多个点，只需要随机确定两个位置，将其视作某一阶段运动的起点和终点，从而探索相互之间的关系，了解变化规律.结合点P在运动过程可能的位置关系，可以作出两个图形，如图4和图5所示.

图4

图5

3.探究

在图4和图5，设P1、P2是P点某一阶段运动的起点和终点，对应的点B1、B2是B的对应运动轨迹的终点.

结论2：∠AB1B2=∠AP1P2.

在图4中，延长B2B1与y轴（直线l）相交于点M，由∠AB1B2=∠AP1P2，可知点A、P1、M、B1四点共圆，所以∠P1MB1=∠P1AB1=90°，所以直线B1B2垂直于y轴.利用相似三角形的性质可知AN的值，AN=atanβ.

在图5中，延长B2B1与y轴（直线l）相交于点M，与AP1相交于点H，连接AM，因为△AP1P2∽△AB1B2，所以∠AB1B2=∠AP1P2，所以点A、M、P1、B1四点共圆.所以∠P1MB1=∠P1AB1=90°.也可以这样证明，如下：因为∠P1AB1=90°，所以∠AHB1+∠AB1B2=90°.因为∠AHB1=∠P1HM（对顶角相等），由等量代换可得∠P1HM+∠AP1P2=90°，所以∠P1MH=90°.所以直线B1B2垂直于y轴.

也可以考虑特殊情形：如图6，当AP1垂直y轴时，AB1=AN，AP1等于点A到y轴的距离，此时AB1=AP1tanβ，点P的位置变化不影响这一结论.

图6

4.建立模型

综合以上分析，可以归纳出以下共性结论，从而建立数学模型：

点P是定直线l上的动点，点A为直线l外一个定点，到直线l的距离为a，当点P在直线l上运动时，以AP为直角边向直线l一侧作Rt△APB，使得∠APB=β，∠A为直角，则有结论：

（1）从动点B的运动轨迹是一条与直线l垂直的直线m，点A到直线m的距离等于atanβ.

（2）从动点B的运动路径长与主动点P的运动路径长之比等于tanβ.

四、回归问题，模型应用

研究后不得不思考一个问题，这种研究的价值何在？最简单的价值体现应该是在解题中的应用，并且需要进行比较，这种数学模型的应用有没有广泛性，问题的解答有没有更加简单.

由模型到实际问题有一定的距离：（1）图形的位置：当数学模型中的直线l为y轴时，可以通过将整个图形绕坐标原点逆时针方向旋转45°，得到原问题中的定直线l；（2）数量关系：将数学模型中的字母具体数字化，回归具体问题，如令∠APB=β=30°.通过这两步，就可以得到图1，实现由问题模型到具体问题的回归、应用.

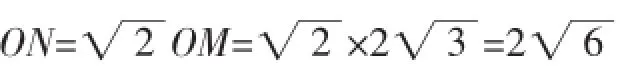
五、数学模型的再优化

回顾前面的数学模型化的过程，发现有一点做得并不充分，那就是对∠APB=90°是否为本质元素的认识存疑.我们可以继续研究更一般的问题：在原有基础上令∠PAB=θ，其他要求不变，数学模型又会发生哪些改变？

如图7和图8，同理可以证明△AP1P2∽△AB1B2，在图7中，∠AB1B2=∠AP1P2，在图8中，∠AB1B2=∠AP1P2，所以点A、M、P1、B1四点共圆.所以∠P1MB1=∠P1AB1=θ.

图7

图8

综上所述，本题数学模型有更一般的形式：

点P是定直线l上的动点，点A为直线l外一个定点，到直线l的距离为a，当点P在直线l上运动时，以AP为直角边向直线l一侧作△APB，使得∠APB=β，∠PAB=θ，则有下面的结论：

（2）从动点的运动路径与主动点的运动路径之比等于tanβ.

1.姜鸿雁.入进去展开来再回首——解答一道中考题的心路历程及感悟［J］.中学数学教学参考（中），2014（10）.

2.庄士忠.相似三角形中三等角题型一般解答方法及应用［J］.中学数学（下），2012（2）.

3.张卫东.利用旋转解题的若干策略［J］.中学数学（下），2011（7）.Z