数形结合思想在高中数学教学中的应用
☉浙江省义乌市上溪中学 陈益民
数形结合思想在高中数学教学中的应用
☉浙江省义乌市上溪中学 陈益民
所谓的数形结合思想,顾名思义,一般来说是数字和图形之间的某些一对一的联系.简要地概括来说,这种数形结合思想说的是把非具体的数学语言、数量之间的联系和直接可以观察到的几何形状、方位关系等联系到一起,利用数学解读形状和利用形状帮助学生理解数学的方法,让比较烦琐的问题变得比较简单,让不是很具体的问题进行具象的描述,用这样的方式来让解决问题的方式变得更加简单.在高中数学的教学中要注意应用这种数字和图形相结合的解答问题的思想,不仅可以让数学问题用图形的方式就能解决,还能够把几何问题转变成为代数问题,这样就能够让高中的学生在数学的学习过程中突破屏障,从而达到解答数学问题的目的.
一、数形结合中数与形的联系及转换方法
1.数与形之间的联系
数形结合的教学思想由以数辅形和以形助数两个部分组成,一部分是运用数的准确性与严密性来表达出形所具有的一些特点及属性,从而推敲出形的关系,例如高中数学教学中以椭圆方程来准确描述出椭圆的特点及性质;另一部分是通过对形的认真观察,直观地得出数量之间的关系,即形是方法,数是最终的解题目的.例如,教学中可以通过函数的图像快速准确地得到图像对应函数的特点及性质.因此,在现实的教学中,教师必须让学生认识到数形结合思想就是将直观的图形和复杂的数量关系相结合,实现数量关系与图形两者之间的转化,从而快速准确地进行解题.
2.数与形之间的转化方法
由数化形是依据题中所给的条件画出正确的图像,可以在图形中得出与题意有关的数量关系,从而很好地完成解题.
由形化数是根据题中所给图形进行认真的观察,来得到数量的关系和几何图形的内在特点.
数形转换是将数与形两者进行的相互转化,学生既可以通过图形的形状特点得到一些数量关系,也可以结合代数式的结构进一步完善图形,从而了解到更多的数量关系.
二、在高中数学教学中渗透数形结合的途径
1.通过深入分析数学概念,渗透数形结合的思想
数学概念是数学学科的基本元素,是建立数学定理、法则、公式的基础,其是感性认识飞跃到理性认识的结果.而飞跃的实现要依据数学思想方法(数形结合作为其中的一种数学思想方法),要经过分析、综合、比较、抽象、概括等思维的逻辑加工而成.因此,在教学中,教师要引导学生,找出事物之间的共同本质属性并用词语把它表示出来,使学生获得概念、体会数学思想和方法.
2.通过例题分析,展示数形结合的思想
例题是展示数学新知识的一个重要组成部分,而例题教学是让学生掌握数学知识、数学思想方法的一个重要途径.通过例题的分析,教师把在问题解决过程中涉及的数形结合思想显性化,使学生能在例题的分析中看到所展示出来的数形结合思想,从而学会应对复杂问题的能力,进而提高自身解决问题的思维策略.
三、“数形结合”在高中数学教学中的具体应用
1.利用韦恩图法解决集合之间的关系问题
一般用圆来表示集合,两圆相交则表示两个集合有公共元素,两圆相离则表示两个集合没有公共元素.利用韦恩图法能直观地解答有关集合之间的关系问题.
例1某班有50人,参加学校举行的甲、乙、丙三科竞赛,选甲的有38人,选乙的有35人,选丙的有31人,兼选甲、乙两门的有29人,兼选甲、丙的有28人,兼选乙、丙的有26人,甲、乙、丙三门均选的有24人,问:此班三门均未选的有多少人?
分析:本题是与集合有关的现实生活问题,此类题一般结合Venn图来解.
解:如图1,选甲、乙而不选丙的有a=29-24=5(人);选甲、丙而不选乙的有b=28-24=4(人);
选乙、丙而不选甲的有c=26-24=2(人);
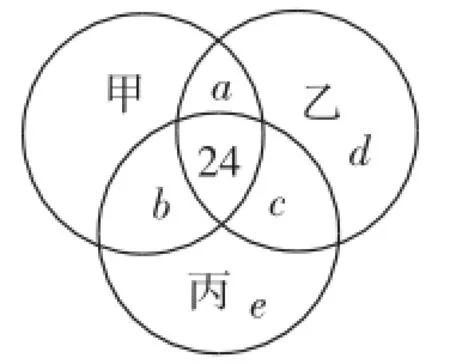
图1
仅选乙的有d=35-24-a-c=4(人);
仅选丙的有e=31-24-b-c=1(人);
至少选了一科的人数是38+d+c+e=45(人).
故三门均未选的人数为50-45=5(人).
2.利用数轴解决集合的有关运算和集合的关系问题
例2设集合M={x|x-1≤x≤7},S={x|k+1≤x≤2k-1},若M∩S=Ø,求k的取值范围.

图2
解析:如图2,在数轴上表示出集合M的范围,要使M∩S=Ø,从而有2k-1<-1或k+1>1,即k<0或k>6.
3.利用二次函数的图像解决一元二次方程根的分布情况问题
根据零点的分布,利用函数图像直观地解决问题.
例3已知关于x的二次方程x2+2mx+2m+1=0,若方程有两个根,其中一根在区间(-1,0)内,另一根在区间(1,2)内,求m的取值范围.
解析:设函数(fx)=x2+2mx+2m+1,则由题意画出示意图,如图3,得:

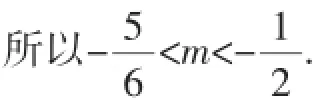

图3
4.利用函数图像解决方程的近似解或解的个数问题
通过构造函数,把求方程解的问题,转化为求两函数图像的交点问题.
例4方程log(2x+2)=的实数解有().
A.0个B.1个C.2个D.3个
分析:由方程可以直接根据数形结合从图像上观察到两函数图像交点的个数,从而推出方程解的个数.

图4
解:令y1=log(2x+2),同一坐标系中,分别画出这两个函数的图像,如图4所示,两个函数图像只有一个交点,所以方程有一个解.故选B.
例5若x满足-3+log2x=-x,则x属于区间().
A.(0,1)B.(1,2)
C.(1,3)D.(3,4)
解析:由-3+log2x=-x得log2x=3-x.在同一坐标系中作出y=log2x和y= 3-x的图像.如图5所示,可观察到这两个函数图像交点的横坐标满足1< x<3.所以选C.

图5
例6如果方程x2+2a+k=0的两个实根在方程x2+ 2ax+a-4=0的两实根之间,试求a与k应满足的关系式.
解析:从图6中可看到,二次函数y1=x2+2a+k,y2=x2+2ax+a-4均是形状相同且有公共对称轴的抛物线,要使方程x2+2a+k=0的两实根在方程x2+2ax+a-4=0的两实根之间,则对应的函数图像y1与x轴的交点应在函数图像y2与x轴的交点之内,它等价于抛物线y1的顶点纵坐标不大于零,且大于抛物线y2的顶点纵坐标.由配方法可知,y1与y2的顶点分别为P1(-a,-a2+k),P2(-a,-a2+a-4),故-a2+a-4<-a2+k≤0.故可求出a与k应满足的关系式为a-4<k<a2.
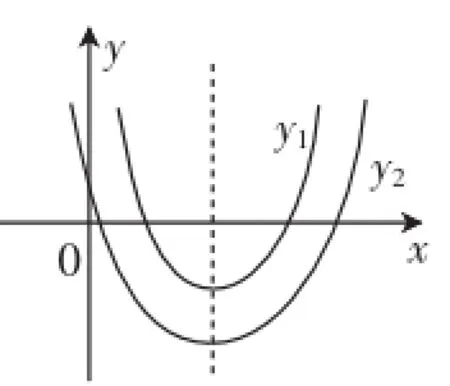
图6
5.利用三角函数的图像解不等式
通过构造函数,把不等式问题转化为两个函数图像的关系问题.
例7解不等式cosx>sinx,x∈[0,2π].

图7
解析:我们可以将不等式的两边表达式看成两个函数y1=|cosx|,y2=|sinx|.在[0,2]上作出它们的图像,得到四|cosx|的图像都在y2=|sinx|的图像上方,所以可得到原不
6.数列中数形结合的应用
数列的难点是如何在具体的问题情境中,发现数列的等差关系,并用有关知识解决相应的问题.而要解决这一难题,则要根据题意画出相应的示意图(或线段图、列表法等),以使学生能迅速地根据图形的性质来分析清楚结论的几何意义等,从而巧用数形结合的思想方法完成解题.

解析:如图8所示,在平面直角坐标系中,点A(cosα,sinα)与点B(cosβ,sinβ)是直线l:ax+by=c与单位圆x2+y2=1的两个交点,故|AB|2=(cosα-cosβ)2+(sinα-sinβ)2= 2-2cos(α-β).又因为单位圆的圆心到直线l的距-

图8
将数形结合运用在高中数学教学中可以使学生的解题思维得到不断发展,增强解题能力,对学生数学思维的发展也有重要影响.数形结合可以利用几何问题映射代数问题,使代数问题与几何问题相互转换,使学生将抽象思维和形象思维结合起来,降低学生解题的难度.此外,数形结合的教学思想已经成为现阶段我国课堂教学的主要手段,数形结合思想的应用使得学生可以方便快捷地抓住解题的关键,提高了学生的解题效率.
1.赵凌岩.数形结合思想在高中数学中的应用[J].课程教育研究(新教师教学),2013(36).
2.宋长江.数形结合思想在高中数学中的应用[J].语数外学习(数学教育),2013(9).A

