风电场短期风速变化区间与变化趋势预测算法

陈 伟，郭建鹏，裴喜平，李恒杰，张 萍，肖 骏

（1.兰州理工大学电气工程与信息工程学院，兰州730050；2.甘肃省电力公司电力科学研究院，兰州730050）

风电是一种间歇性能源，具有强波动性、同步强随动性、出力动态特性的功率弱支撑性等特点。准确地预测风速可以充分发挥风电场的作用，减轻风电对电网的不利影响。对短期风速区间的预测是增强电网的安全性和可靠性，实现电网调度部门合理经济调度的有效手段[1-2]。

根据是否使用气象数据，短期风速预测方法可分为两类：一类是使用数值气象预报的预测方法，有统计模型和物理模型；另一类是基于历史数据的预测方法。由于实际应用中数值气象预报模型无法获得或者缺失，对风速短期预测主要是基于历史数据的研究方法。基于历史数据的预测方法有：持续预测法[3]、卡尔曼滤波法[4]、时间序列法[5-6]、支持向量机法[7-8]、人工神经网络法[9]等。现有的风速预测方法大多得到的是具体的风速预测值，而对风速变化区间与变化趋势的研究较少。若能对风速的变化区间进行预测，则能反映下一时段风速的变化范围，可使电力调度人员更好地了解未来风速的波动范围，因此研究风电场风速的变化区间和变化趋势具有重要的实用价值和理论意义。

本文提出了一种基于模糊信息粒化和最小二乘支持向量机FIG-LSSVM（fuzzy information granulation-least squares support vector machine）的风速区间预测算法，对风电场风速的变化区间和变化趋势进行预测。根据甘肃酒泉地区某风电场实测数据，对风速时间序列进行模糊信息粒化，利用最小二乘支持向量机预测模型进行回归预测，仿真分析结果表明，该算法可以有效地预测风电场短期风速的变化区间和变化趋势。

1 模糊信息粒化

信息粒化IG（information granulation）的概念最早是由Zadeh 教授提出来的，它将一个整体分解为几个部分进行研究，每个部分为一个信息粒，信息粒就是一些元素的集合，这些元素从本质上讲是通过相似性、功能近似性、不可区分性、函数性等来划分的对象集合。粒化计算是当前计算智能研究领域中模拟人类思维和解决复杂问题的新方法[10-11]。

模糊信息粒化FIG（fuzzy information granulation）利用模糊理论对不确定知识的处理能力，将模糊集理论引入粒计算模型中。基于模糊信息粒计算理论的推理、决策和识别方式是以贴近人类思维形式的方式来解决问题。人类利用模糊信息粒化以便在不完全知识、部分确定以及部分真实的环境中作出合理决策的方法，被视为机器智力的原型。

模糊信息粒可以用粒的一般模型表示为

式中：A 为论域；F 为A 到[0，1]的映射。

对时间序列进行模糊信息粒化的步骤如下。

（1）划分窗口。划分窗口就是将时间序列分割成若干个小子序列，每一小子序列作为一个操作窗口；

（2）模糊化。模糊化就是将产生的每一个窗口进行模糊化，生成一个个模糊集，也即模糊信息粒。

其中最为核心的是模糊化的过程，因为对窗口进行模糊化后，必须建立合理的模糊集，使该模糊集可以代替原来窗口中的数据，满足研究者的需求，该模糊集能够反映出人们所关心的信息。

本文采用Witold Pedrycz 的模糊粒化方法[12]。首先把时间子序列看成是一个操作窗口，记为A；在A 上建立一个模糊粒子，该模糊粒子能够较为全面地描述A 的模糊概念G（以A 论域的模糊集合）。如此以来，确定了模糊概念G，也就确定了模糊粒子P，即

模糊化过程本质上就是确定函数f 的过程，f是模糊概念G 的隶属函数，模糊粒子P 可以代替模糊概念G，即P 可简单描述为

典型的三角模糊粒子其隶属函数为

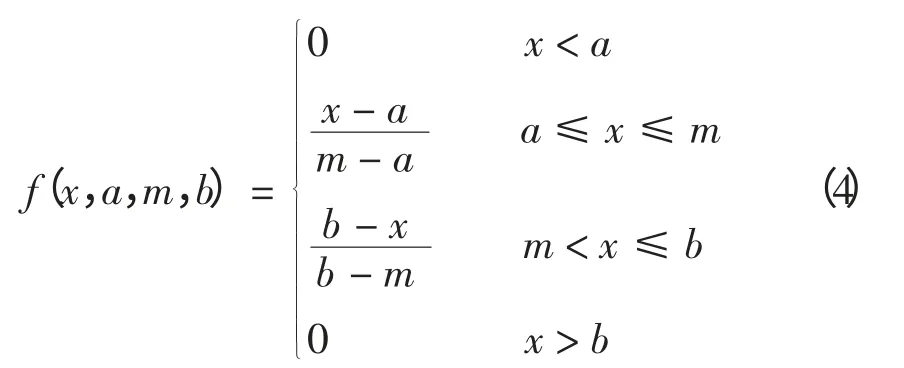
无论使用何种形式的模糊集来建立模糊粒子，模糊粒子要有一定的特殊性并且能够合理表示原始数据的信息。为找到两者的最佳平衡，可考虑建立关于f 的一个函数，即

式中：Mf满足建立模糊粒子合理性；Nf满足建立模糊粒子的特殊性。

以单窗口为例介绍如何对时间序列进行模糊粒化，采用三角模糊集为模糊粒子，其步骤如下。

步骤1 首先确定三角模糊集的核m。将时间序列X=（x1，x2，…，xn）按照从小到大的顺序进行排列，排完后的序列仍记为X=（x1，x2，…，xn）。当n为偶数时，m=xn/2；当n 为奇数时，m=xn+1/2。

步骤2 确定三角模糊集的支撑下界，即

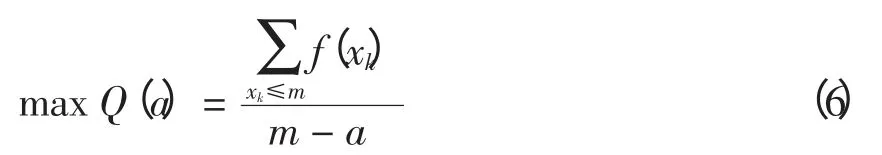
步骤3 确定三角模糊集的支撑上界，即

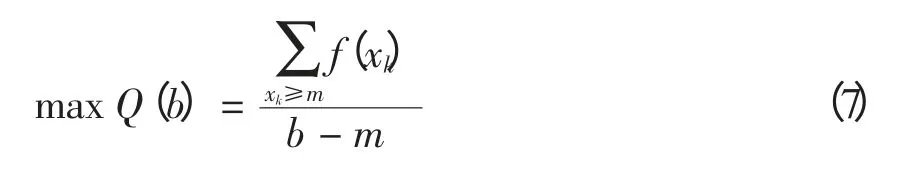
步骤4 最后得出模糊粒子。

利用上面的步骤可以求出对时间序列X =（x1，x2，…，xn），所建立的模糊粒子为

式中：f（m）=1；f（a）=f（b）=0。

以上是对单窗口的模糊粒化方法。同样地，对于多窗口的模糊粒化，需对每一个窗口进行模糊粒化即可[13]。

2 最小二乘支持向量机预测模型

运用SVM 对风速时间序列预测，有时会出现训练速度慢、内存开销大等问题。最小二乘支持向量机LS-SVM（least squares support vector machine）是支持向量机SVM（support vector machine）的一种改进，它将传统的支持向量机中的不等式约束改为等式约束，将误差平方和损失函数作为训练集的经验损失，把求解二次规划问题转化为求解线性方程组问题，简化了运算算法，提高了求解问题的速度和收敛精度[14]。

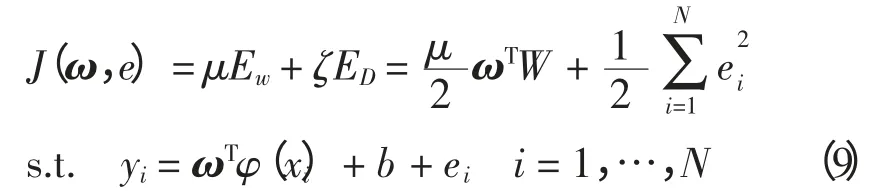
式中：φ（·）：Rm→Rn为核空间映射函数；ω 为权矢量，ω∈Rn；ei为误差变量，ei∈R；b 为偏置量；μ 和ζ为可调参数。

为求解优化函数的最小值，构造Lagrange 函数，即

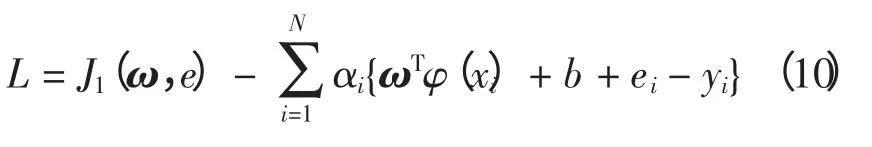
式中，αi为拉格朗日乘子。

对式（10）求偏导，并令偏导数等于0，得

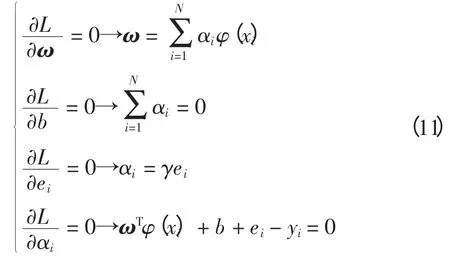
消去ω 和e 后，求解的优化问题可转化为线性方程，即

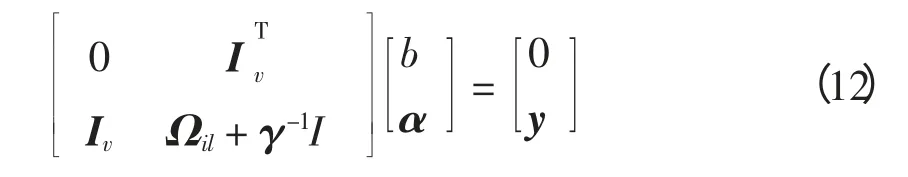
式中：Iv= [1，2，…，l]T；y =（y1，y2，…，yN）T；α =（α1，α2，…，αN）T；Ωil=φ（xi）Tφ（xl）；I 为N×N 单位阵。

通过求解式（12）可得到α 和b，根据Mercer条件，存在映射函数φ（·）和核函数k（·，·），使得

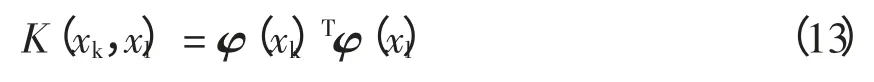
得到的LS-SVM 的回归函数为

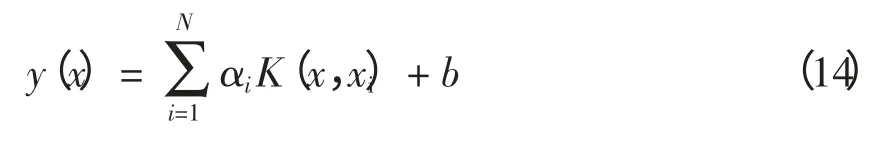
其中，应用高斯径向基核函数为

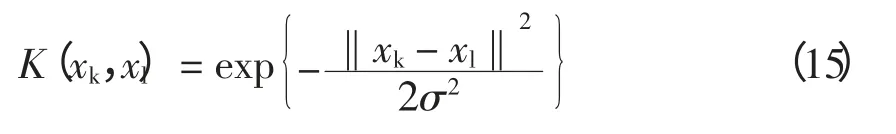
3 实例分析

以甘肃酒泉某风电场2012 年8 月的实测风速时间序列作为实验样本，对本文所提出的算法进行了验证。样本数据在0801T00∶00—0808T07：00 之间，每15 min 作为一个采样点，共计700 个风速数据预测未来75 min 内风速的变化区间和变化趋势，如图1 所示。

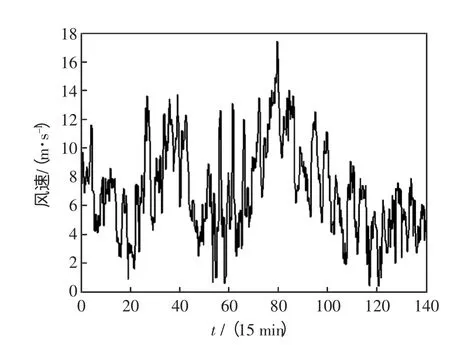
图1 风速时间序列Fig.1 Time series of wind speed

将模糊信息粒化和最小二乘支持向量机的优点结合起来，提出了基于FIG-LSSVM 的风速区间预测算法。选取风电场的实测风速数据，对所选取的数据进行Witold Pedrycz 模糊信息粒化，得到3个模糊粒子Low、R 和Up，对这3 个模糊粒子利用LSSVM 预测模型进行回归预测，其预测流程见图2。

采用三角模糊粒子，进行模糊信息粒化。将原始数据划分为多个窗口，每一个窗口将生成一个模糊粒子，以5 个数据作为一个窗口的大小，对风速时间子序列进行模糊信息粒化后如图3 所示。模糊粒化后有3 个参数：Low、R 和Up，对于三角模糊数而言，Low、R、Up 即为a、m、b 参数。其中对于单个模糊粒子而言，Low 参数表示的是相应原始数据中的最小值，R 参数表示的是相应原始数据的变化趋势，Up 参数表示的是相应原始数据中的最大值；预测结果Low′代表风速区间变化的下限值，R′表示风速预测区间的变化趋势，Up′表示风速区间变化的上限值。

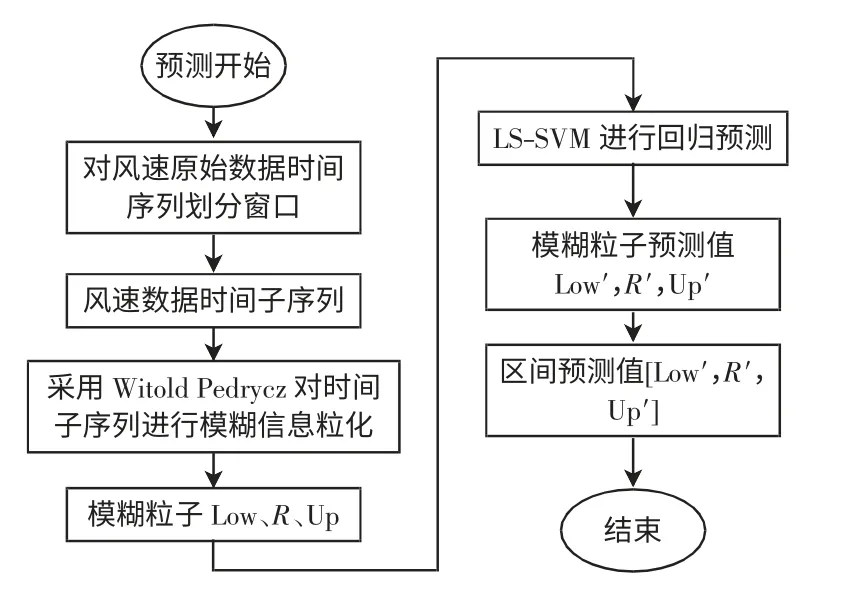
图2 基于FIG-LSSVM 的风速区间预测流程Fig.2 Flow chart of interval prediction of wind speed based on FIG-LSSVM

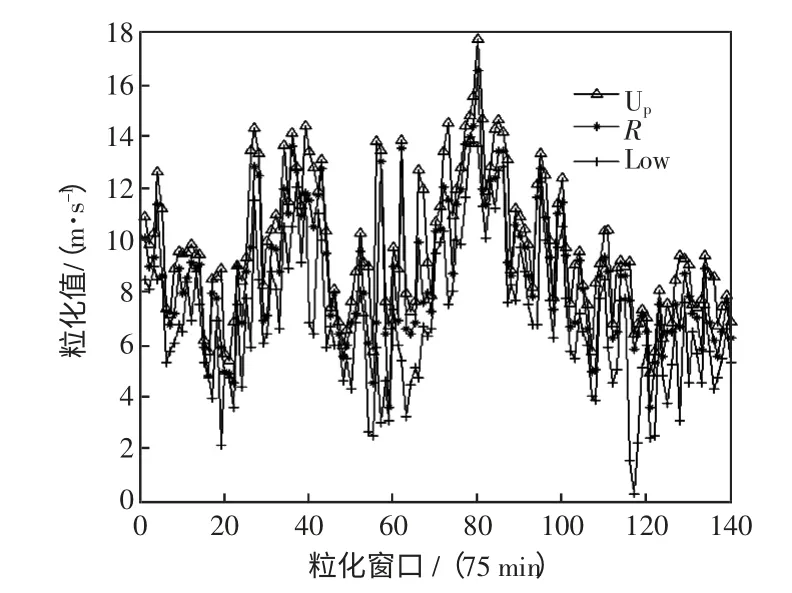
图3 风速序列的模糊信息粒化可视图Fig.3 Visualization of fuzzy information granulation of wind speed sequence

以Up 参数预测为例，将最小二乘支持向量机（LS-SVM）预测模型、支持向量机（SVM）预测模型和BP 神经网络预测模型对模糊粒子Up 变量的预测结果做了比较，如图4 所示。LS-SVM 和SVM 预测模型均选取径向基核函数（RBF）作为模型的核函数，运用粒子群算法对核函数中的核参数和正规化参数进行优化[15]。

用Up1表示实测数据，Up2表示预测值，预测的绝对误差为Error=Up2-Up1。图5 为采用不同的预测模型时Up1变量的预测绝对误差。

从图5 可以看出，对Up1变量进行预测时，LSSVM 预测模型与SVM 和BP 网络预测模型相比，预测精度有较大的提高。这是因为对模糊粒子进行回归预测时，BP 神经网络容易陷入局部极值，需要的训练数据多，收敛速度慢；支持向量机预测模型收敛速度和最优性等方面优于BP 神经网络模型，但仍有待提高；而最小二乘支持向量机简化了运算算法，进一步提高了运算速度与收敛精度。评价指标如表1 所示。

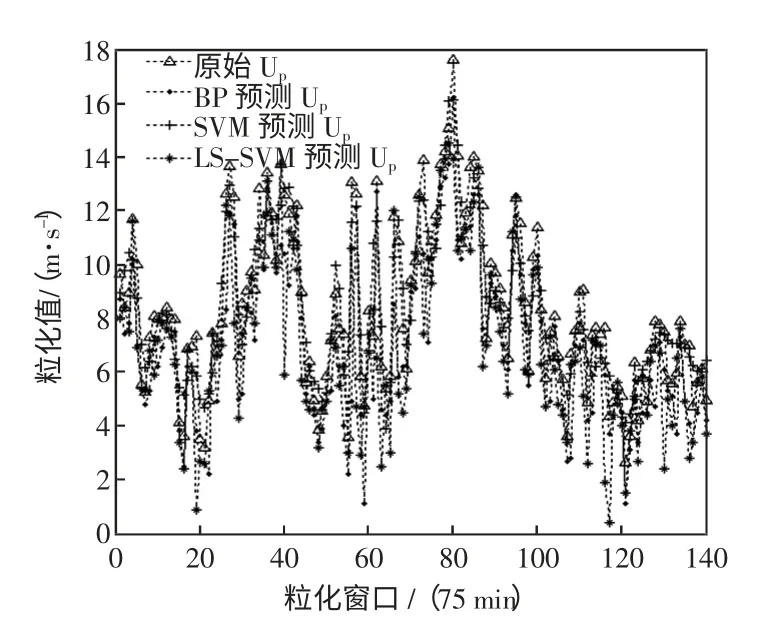
图4 Up 变量不同预测值与真实值的比较Fig.4 Comparison between different predicted value and true value of Up

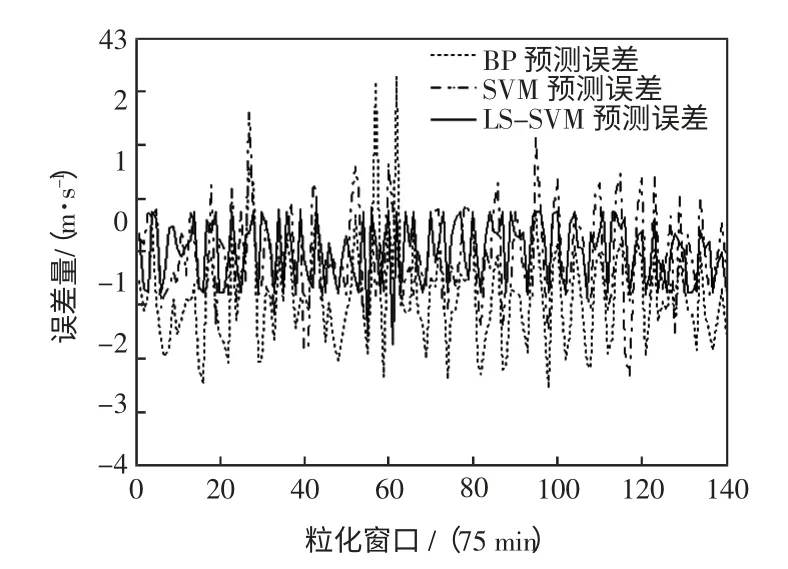
图5 不同模型的Up 变量预测绝对误差Fig.5 Absolute errors of Up predicted of different models

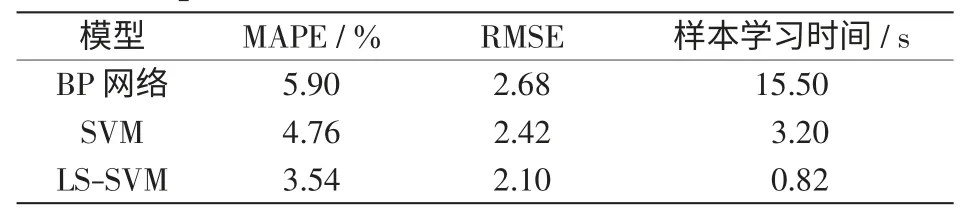
表1 不同模型的Up 变量预测的评价指标值Tab.1 Evalution index value of different models of Up prediction

同理，采用Witold Pedrycz 对风速时间序列模糊信息粒化得到Low 和R 的模型参数，然后再用LS-SVM 预测模型分别对Low、R 进行回归预测，预测结果如图6 和图7 所示，得到风速区间预测的最小值和变化趋势，综合Low、R 和Up 的预测值从而得到0808T07∶00—0808T08∶15 整个短期风速区间的预测值。

通过表2 可以看出：与前5 个时刻的风速序列相比，风电场风速有整体上升的趋势，并且后5个时刻的风速序列都在预测范围内，表明本文所提算法具有较好的预测能力。

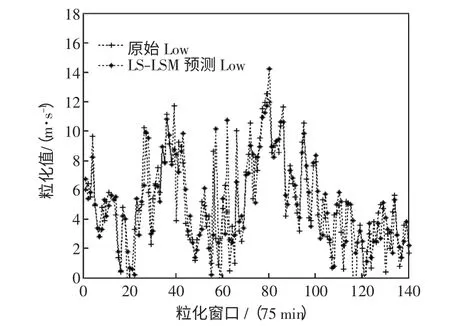
图6 Low 变量的真实值与LS-SVM 预测值Fig.6 True values of Low and predicted value based on LS-SVM

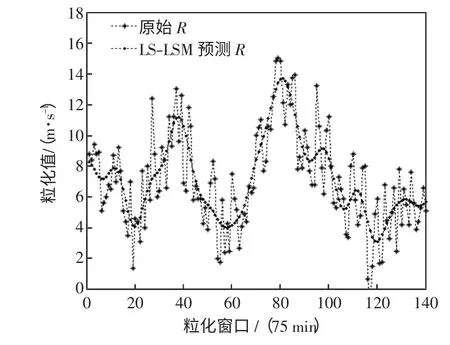
图7 R 变量的真实值与LS-SVM 预测值Fig.7 True value of R and predicted value based on LS-SVM

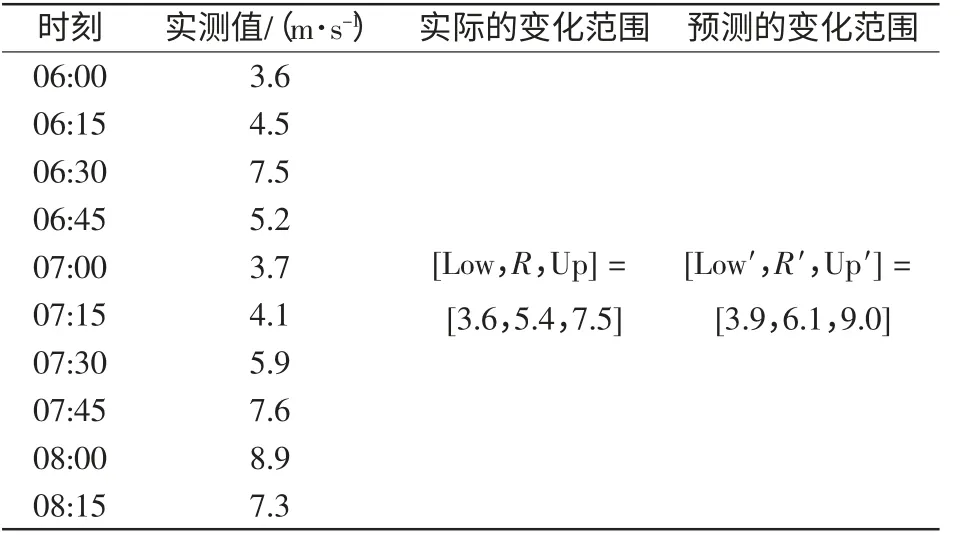
表2 风电场风速变化区间和变化趋势的预测结果Tab.2 Prediction result of the change interval and change trend of wind speed

4 结语

风电场风速区间预测的结果不是一个简单的确定性数值，而是一个区间，能描述未来预测结果的可能范围。根据变化区间预测结果，电力系统决策人员在进行生产计划、系统安全分析等工作时能够更好地认识到未来系统可能存在的不确定性和面临的风险因素，从而及时作出更为合理的决策。本文将模糊信息粒化应用到非线性、时变的风速时间序列预测中，采用最小二乘支持向量机进行回归预测，得到了短期风速的变化区间和变化趋势，提高了预测精度和收敛速度。算例证明FIGLSSVM 预测算法有较高的预测精度和效率，能够满足实际应用要求。

[1]尹明，王成山，葛旭波（Yin Ming，Wang Chengshan，Ge Xubo）. 风电并网经济技术评价研究综述（Review of economic technical assessment of wind power integration）[J].电力系统及其自动化学报（Proceedings of the CSUEPSA），2010，22（5）：102-108.

[2]杜颖，卢继平，李青，等（Du Ying，Lu Jiping，Li Qing，et al）.基于最小二乘支持向量机的风电场短期风速预测（Short-term wind speed forecasting of wind farm based on least square-support vector machine）[J]. 电 网 技 术（Power System Technology），2008，32（15）：62-66.

[3]蒋小亮，蒋传文，彭明鸿，等（Jiang Xiaoliang，Jiang Chuanwen，Peng Minghong，et al）.基于时间连续性及季节周期性的风速短期组合预测方法（A short-term combination wind speed forecasting method considering seasonal periodicity and time-continuty）[J].电力系统自动化（Automation of Electric Power Systems），2010，34（15）：75-79.

[4]Louka P，Galanis G，Siebert N，et al.Improvements in wind speed forecasts for wind power prediction purposes using Kalman filtering[J]. Journal of Wind Engineering and Industrial Aerodynamics，2008，96（12）：2348-2362.

[5]丁明，张立军，吴义纯（Ding Ming，Zhang Lijun，Wu Yichun）. 基于时间序列分析的风电场风速预测模型（Wind speed forecast model for wind farms based on time series analysis）[J].电力自动化设备（Electric Power Automation Equipment），2005，25（8）：32-34.

[6]陈国初，杨维，张延迟，等（Chen Guochu，Yang Wei，Zhang Yanchi，et al）.风电场风速概率分布参数计算新方法（New computation method of wind speed probability distribution parameters in wind farm）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（1）：46-51.

[7]Wang Xiaolan，Li Hui. One-month ahead prediction of wind speed and output power based on EMD and LSSVM[C]//International Conference on Energy and Environment Technology.Guilin，China，2009：439-442.

[8]戚双斌，王维庆，张新燕（Qi Shuangbin，Wang Weiqing，Zhang Xinyan）.基于支持向量机的风速与风功率预测方法研究（Wind speed and wind power prediction based on SVM）[J].华东电力（East China Electric Power），2009，37（9）：1600-1603.

[9]黄小华，李德源，吕文，等（Huang Xiaohua，Li Deyuan，Lü Wen，et al）. 基于人工神经网络模型的风速预测（Wind speed forecasting with artificial neural networks model）[J].太阳能学报（Acta Energiae Solaris Sinica），2011，32（2）：193-197.

[10]李鸿（Li Hong）.粒集理论：粒计算的新模型（Theory of granular set：A new model of granular computing）[J]. 重庆邮电大学学报：自然科学版（Journal of Chongqing University of Posts and Telecommunications：Natural Science），2007，19（4）：397-404.

[11]黄兆华，邓毅雄（Huang Zhaohua，Deng Yixiong）.粒计算及其应用的研究（An approach for granular computing and its application）[J]. 华东交通大学学报（Journal of East China Jiaotong University），2005，22（5）：124-128.

[12]Witold Pedrycz. Knowledge-Based Clustering From Data Information Granules[M]. New York：John WileY & Sons Inc，2005.

[13]张翔宇（Zhang Xiangyu）.基于优化BP 神经网络和粒计算的股指预测研究（The Research of Stock Composite Index Prediction Based on Optimized BP Neural Network and Granular Computing）[D].南京：南京大学工程管理学院（Nanjing：School of Management and Engineering，Nanjing University），2012.

[14]张浩然，汪晓东（Zhang Haoran，Wang Xiaodong）. 回归最小二乘支持向量机的增量和在线式学习算法（Incremental and online learning algorithm for regression least squares support vector machine）[J].计算机学报（Chinese Journal of Computers），2006，29（3）：400-406.

[15]孙斌，姚海涛，刘婷（Sun Bin，Yao Haitao，Liu Ting）. 基于高斯过程回归的短期风速预测（Short-term wind speed of forecasting based on Gaussian process regression model）[J].中国电机工程学报（Proceedings of the CSEE），2012，32（29）：104-109.