同杆双回线的反序负序纵联距离保护新方法

司泰龙，牛 林，王睿昕，战 杰，郭其一，田 羽

（1.国网技术学院电网检修培训部，济南250002；2.山东理工大学电气与电子工程学院，淄博255000；3.同济大学电气工程系，上海201804；4.上海电力设计院，上海200025）

同杆双回线因具有输送容量大、节约线路走廊等优点，在220 kV 及以上电压等级系统中已得到积极应用。其中，纵联距离保护是同杆并架双回线中重要的保护之一，其距离测量元件不仅具有明确的方向性，而且有固定的动作范围。但是由于双回线路的特殊结构，零序互感、过渡电阻、系统运行方式等因素使得距离继电器不能正确反映故障距离，导致保护出现超越或拒动现象[1-3]。

目前，在对多种类型距离保护的性能分析和探讨中，文献[4]针对性地提出了六相序阻抗距离保护，能够准确反映故障距离，但所需测量元件繁多，实现起来较为困难；文献[5]则提出在双回线中利用零序分量判断故障回线，并能准确反映单相接地故障，但不适用于相间故障和跨线故障；文献[6]也提出了一种基于零序分量的距离继电器，尤其对于现场较易出现的电压回路异常等情况仍能正常工作，但主要适用于单回线路的保护[5]。

本文提出了一种改进序分量距离保护原理。该原理将同杆双回线路看作一个保护单元，利用六序分量法获取反序负序分量，进而得到一种新型纵联距离保护判据。该判据获取判据量简便，对双回线中的单回线故障与跨线故障消除了零序互感对保护的干扰；同时耐过渡电阻能力强，不局限于接地故障和不接地故障，且该原理也适用于带有弱馈系统的同杆双回线。在系统发生不对称故障时，若配合先进的选相元件和通讯通道，该保护可作为智能电网中同杆双回线的主保护。

1 同杆双回线中反序负序分量的特征

同杆双回线系统如图1 所示，其特点是相间、线间有互感。六序分量法将两回线分解为六序对称分量，以消除相间、线间互感对保护的影响[7]。以六序分量法为基础的反序电流是双回线故障的显著特点，对其研究有利于深入了解同杆双回线特点。反序电流又称环流电流，仅存在于发生内部故障的双回线中，不流经过渡电阻和系统电源，故双回线外部的过渡电阻、系统电源等因素对于反序电流无作用。且反序分量只存在于双回线内部故障，双回线外故障时为0（无论双回线参数是否对称），据此判断故障是否位于双回线中。

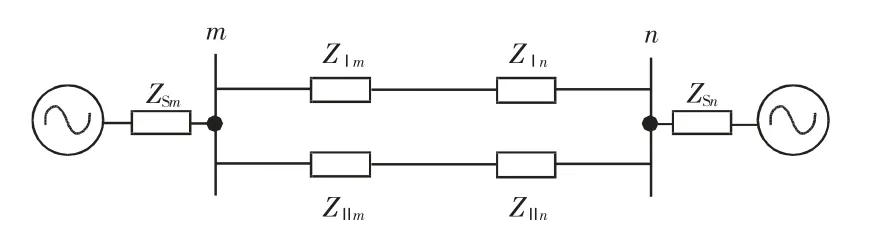
图1 同杆双回线系统Fig.1 System of double parallel transmission lines on same tower

同杆双回线反序负序分量网络如图2 所示。当系统内部故障时，故障点的反序负序电压最大，且反序负序分量的系统阻抗为0，所以双回线两端的反序负序电压为0[7]，故线路两端的反序负序电流不会受到分布电容电流的影响。同时，因采用的是两回线中的负序分量，故可以很好地克服系统振荡对保护的影响。另外，反序负序电流是故障后的序分量电流，与传统的零序电流、负序电流相同，整定时无需考虑非周期分量、负荷电流的影响[8]。

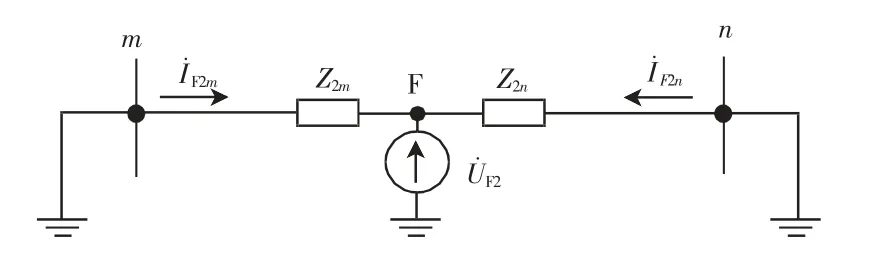
图2 同杆双回线反序负序分量网络Fig.2 Inverse directional negative sequence component network chart of double-circuit transmission line

2 基于反序负序分量的距离保护

2.1 基于反序负序分量的距离保护原理

假定线路阻抗均匀一致，当等效双回线路发生故障时，则对应反序负序网的电压分布如图3所示。其中，f1为保护区内故障点，f2为正向区外故障点，y 为m 侧的整定点，且m 侧、n 侧测得的反序负序电压分别为曲线k1、k2。同时，根据上述反序负序分量的特征分析，理论上在系统正常情况和双回线mn 外故障时，反序负序电流为0，相应整定点电压也为0[9]。

由此可得，对于保护安装处m 点，同杆双回线反序负序分量距离继电器的动作方程为

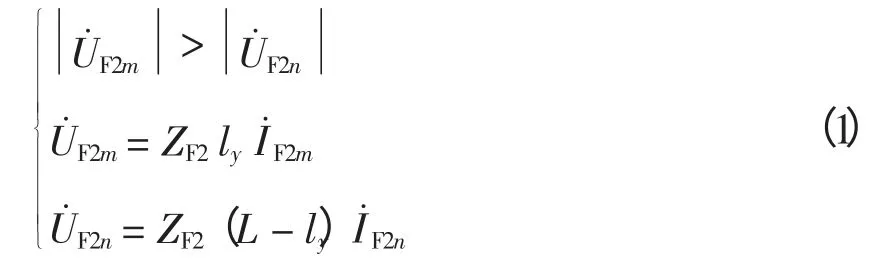
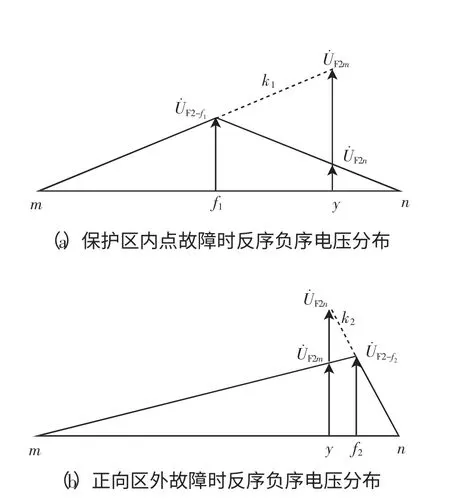
图3 基于反序负序分量的距离保护原理示意Fig.3 Distance protection schematic based on inverse directional negative sequence component

2.2 基于反序负序分量的距离保护的实现

基于反序负序分量的距离保护动作方程确定后，需要考虑该保护的实现方法。因反序负序分量不受系统振荡、电容电流等因素的影响，故需考虑躲开双回线外部故障时，两侧电流互感器的产生的最大不平衡电流。以m 侧为例分析，由文献[7]可以得到反序负序电流的表达式为

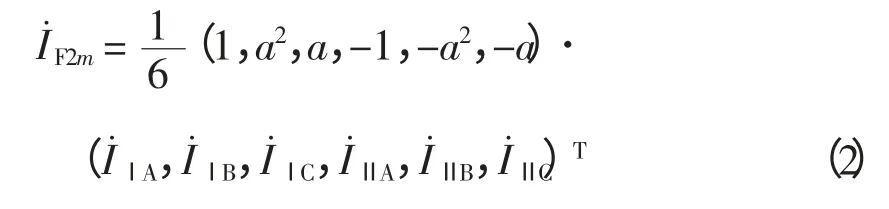
因此，基于反序负序分量的距离保护的实现不仅需要满足动作方程式（1），而且需躲开区外故障时不平衡电流的影响，即

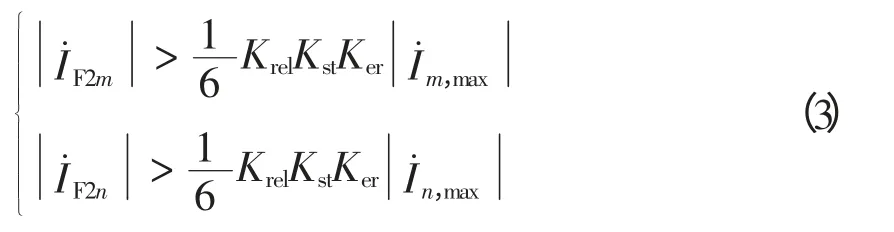
式中：Krel为可靠系数，取1.2～1.3；Kst为TA 同型系数，TA 型号相同时取0.5，否则取1；Ker为TA 误差系数，取10%；分别为m、n 侧最大单相短路电流。

2.3 基于反序负序分量的距离保护性能分析

传统的方向距离保护常采用故障点电气量作为制动量，但该量的准确获取成为制约传统保护研究的主要因素。文献[5]选取故障后测得的电气量，利用整定系数确定故障点电压值，但这种计算值很不准确；文献[10]以整定范围末端故障后的量作为动作的定值，由序网图得到故障点处的电气量，实际上也不精确。本文利用保护装设端与对端的反序负序电流，求得整定点反序负序电压作为判据量，即以保护安装端反序负序分量为动作量，以对端反序负序分量为制动量，避开了传统保护中因故障点信息无法准确获取而误判的弊端，并附加测量误差方程，使保护更加可靠、准确。

由图3 得，对于保护区内故障（f1点），按式（1）求出m、n 侧在整定点处的反序负序电压，m 侧电压即曲线k1延长线上的整定点电压量，因线性关系，从而使动作方程满足；对于正向区外故障（f2点），按式（1）求出m、n 侧电压量，n 侧电压即曲线k2延长线上的整定点电压量，不满足动作方程，保护不会误动。此外，对于区外故障，因反序负序电流良好特性，保护区段内其理论值为0，但也会出现因测量误差而满足式（1）的假象，所以辅助判据方程式（3）很好地避免此类情况的发生。

由于利用了反序负序分量作为保护动作判据，该判据消除了零序互感与过渡电阻对距离保护的影响，且受负荷电流、系统振荡、系统运行方式的因素影响也很小，同时又考虑到电源两侧不平衡电流的影响，从而具有很好的动作性能。

2.4 反序负序距离保护对于带弱馈系统的同杆双回线的适用性

在电网中部，同杆双回线路所处的背端支撑电源一般都较强，而在电网的外围、终端，线路所依靠的系统强弱差异很大，即会出现带弱馈系统的情况。由于弱电源侧系统阻抗很大，故障电流很小，极有可能因不能提供足够的短路电流而使距离保护装置无法启动，从而影响了电网供电可靠性，甚至危及电网安全[11]。

由图2 可见，在反序负序分量网络图中，线路两端的系统阻抗为0，故可以削弱具有较大系统阻抗的弱馈系统对距离保护的影响，辅助判据量不会因系统阻抗增大而锐减，使保护可靠躲开不平衡电流。而且，因该距离保护同时具有针对普通双回线的优点，所以十分适用于带弱馈系统的同杆双回线路。

3 基于反序负序分量的纵联距离保护

上述距离保护仅能在本线路的80%～85%长度范围内故障时动作，而其余15%～20%无法得到保护。然而，可以在反序负序分量距离保护的基础上，增加通信接口和必要的动作逻辑实现纵联距离保护，达到可靠保护全线的目的。

因上述反序负序距离保护可以灵敏地判断故障区段，且适用于弱馈系统，故可利用欠范围直接跳闸式的纵联保护方式来保护全线，如图4 所示[12]。线路两端的欠范围整定动作范围要相互交叉。在正常运行情况下，m 端、n 端的发信机各发出一种闭锁对端和通信连续监视的闭锁频率信号。在线路内部任一点发生故障时总有一端保护动作，动作后立即直接跳开本端线路断路器，控制发信机将闭锁频率信号切换成跳闸频率信号；未跳闸一端接收到此跳闸频率信号后，通过“或”门跳开本端断路器。该方法使用元件少，内部故障时保护动作速度快。该纵联距离保护融合了纵联电气量和纵联逻辑信号两种纵联保护原理。首先，向对端传输该端的电气量，经新的纵联距离保护原理判断后，再向对端传输逻辑信号，做出最终判断。

同时，由于该距离保护本身无选相功能，故障后如需选跳，则应与另外的选相元件配合以形成整体保护方案。

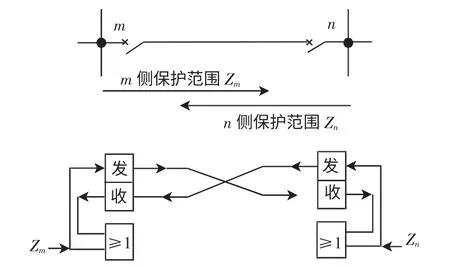
图4 基于反序负序分量的纵联距离保护逻辑框图Fig.4 Longitudinal distance protection logic diagram based on inverse directional negative sequence element

4 EMTP 仿真与分析

4.1 仿真模型及结果

系统模型如图1 所示，电压等级为220 kV，被保护线路全长为100 km，n 侧为线路保护的弱电源侧。母线m 侧背后的系统参数为：Z1Sm=0+j8 Ω，Z0Sm=0+j4.16 Ω，弱馈侧参数为：Z1Sn=853+j2 800 Ω，Z0Sn=263.2+j1 895 Ω，单回线的线路阻抗ZL1=0.034 16 + j0.347 8 Ω/km，ZL0= 0.058 21 + j0.400 8 Ω/km，双回线间零序互感ZM=0.03+j0.581 2 Ω/km，线路导纳Y1=1.663×10-5S/km，Y0=2.120×10-5S/km。距离继电器的整定范围为线路全长的80%，且两端电源的电势夹角φ 在0°～60°范围内变化（m 端超前）。

仿真结果显示，线路不同区段发生各种故障如单回线路故障ⅠA、ⅠBC，跨线故障ⅠBⅡC、ⅠAⅡBC、ⅠAⅡABC、ⅠBCⅡABC）时，对于接地故障（直接接地和经过渡电阻为200 Ω）和不接地故障，该纵联距离保护均能正确动作。当距端0～20 km内故障，m 侧保护检测到故障，并带动n 侧动作；当距m 端20～80 km 内故障，m 侧、n 侧均能检测到故障，并准确动作；当距m 端80～100 km 内故障，n侧保护检测到故障，并带动m 侧动作；当故障发生在线路mn 范围外时，因无法满足辅助判据式（4），两侧保护均不动作。

4.2 反序负序纵联距离保护的性能分析与验证

分别在3 种故障情况下，基于反序负序纵联距离保护进行仿真，仿真结果如图5～图7 所示，其中φ=60°，t=0.01 s 时发生故障。图中纵坐标U˙即判据公式中的

故障情况1：图5 为距m 端75 km 处ⅠA_G故障时，m、n 侧保护装置的动作量和制动量曲线。由图可以看出，m 侧保护虽然处于保护范围末端，但仍能可靠满足动作方程；n 侧保护更易满足判据方程，从而使纵联保护动作，两侧保护对其构成冗余系统。因此该保护原理可靠性较高。

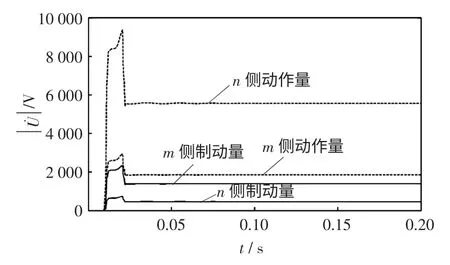
图5 距m 端75 km 处ⅠA 金属性接地故障时仿真结果Fig.5 Simulation results of ⅠA phase grounding by metallic resistance 75 km from m

故障情况2：图6 为距m 端25 km 处ⅠBC 故障，经过渡电阻（Rg=200 Ω）与金属性接地情况下m 侧保护的判据值曲线。由图5 看出，在上述2 种接地情况中，保护测得的动作量制动量曲线相差不大，即该保护不因过渡电阻的存在而受干扰，抗过渡电阻能力强。

故障情况3：图7 为距端50 km 处ⅠAⅡBC 故障时m、n 侧保护装置的动作量和制动量曲线。因m 侧为大电源，n 侧为弱电源，即对于背侧为大电源与弱电源情况，距故障点相同距离时，保护所测得的动作量与制动量的曲线完全重合，故该保护原理不受带弱电源的影响，避免了弱馈系统锐减短路电流的作用，适用于弱馈系统。

5 结语

本文利用六序分量法，提出了一种适用于同杆双回线的反序负序纵联距离保护新原理。由于反序负序分量存在于不对称故障的全过程，所以反序负序纵联保护能可靠地反映不对称故障，即对于双回线中，除单回线对称故障和同名相跨线故障外，发生不对称的单回线故障与跨线故障时，不仅消除了零序互感的干扰，且抗过渡电阻能力强，同时对于弱馈系统具有很好的适用性。理论分析与大量的EMTP 仿真试验证明，此纵联距离保护在智能电网领域具有良好的性能。

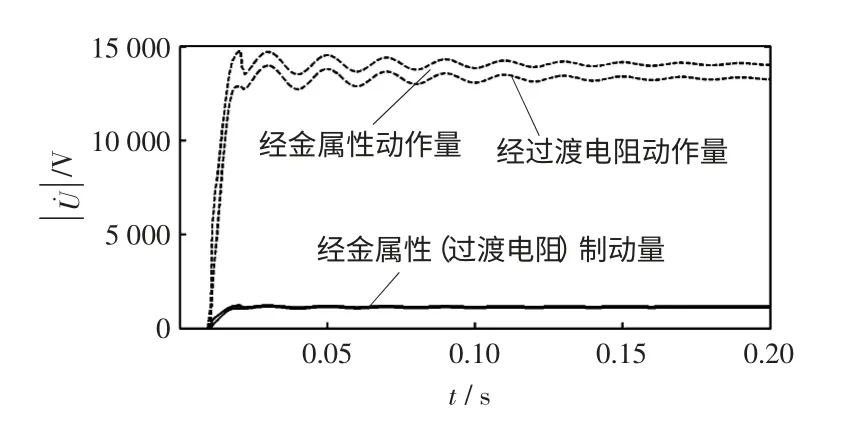
图6 距m 端25 km 处ⅠAⅡBC 经过渡电阻与金属性接地故障时仿真结果Fig.6 Simulation results of ⅠAⅡBC phase grounding by fault resistance and metallic resistance 25 km from m

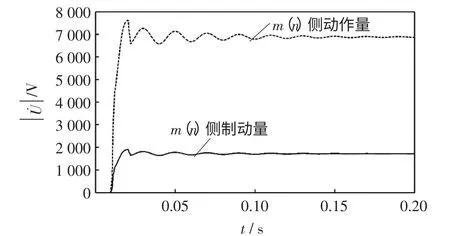
图7 距m 端50 km 处ⅠAⅡBC 故障仿真结果Fig.7 Simulation results of ⅠA ⅡBC phase fault 50 km from m

[1]冯勇鑫，温渤婴（Feng Yongxin，Wen Boying）.接地距离保护中零序补偿系数整定方法的探讨（Investigation on setting method for zero-sequence current compensation coefficient in ground-fault distance protection）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2008，20（3）：95-98.

[2]周璐，黄纯，张秋丽，等（Zhou Lu，Huang Chun，Zhang Qiuli，et al）. 基于SVD-prony 的消除暂态超越的新算法（A novel algorithm for eliminating transient overreach based on SVD-prony）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（4）：122-127.

[3]肖伟强，蔡泽祥，刘为雄，等（Xiao Weiqiang，Cai Zexiang，Liu Weixiong，et al）.同杆线路零序互感对纵联距离保护的影响（Influence of zero sequence mutual inductance on the pilot distance relay in multi-circuit transmission lines）[J].电力系统自动化（Automation of Electric Power Systems），2009，33（3）：84-88.

[4]孟远景，鄢安河，李瑞生，等（Meng Yuanjing，Yan Anhe，Li Ruisheng，et al）.同杆双回线的六相序阻抗距离保护方案研究（The study on six phase sequence distance relay protection scheme for double-circuit lines on the same pole）[J].电力系统保护与控制（Power System Protection and Control），2010，38（6）：12-17.

[5]邓妍，邰能灵（Deng Yan，Tai Nengling）.适用于平行双回线路的零序距离继电器研究（Study of the double lines distance relay based on zero sequence components）[J].华东电力（East China Electric Power），2006，34（2）：103-106.

[6]毛鹏，杨立璠，杜肖功（Mao Peng，Yang Lifan，Du Xiaogong）.基于零序分量的距离继电器（Study of the distance relay based on zero sequence components）[J]. 电力系统自动化（Automation of Electric Power Systems），2003，27（10）：60-62，66.

[7]葛耀中.新型继电保护和故障测距的原理与技术[M].西安：西安交通大学出版社，2007.

[8]郭强，尚海一（Guo Qiang，Shang Haiyi）.负序方向元件在同杆双回线中的动作行为分析（Analysis of negative sequence directional element behavior in double lines on same tower）[J].电力自动化设备（Electric Power Automation Equipment），2010，30（12）：83-87.

[9]田羽，范春菊，龚震东，等（Tian Yu，Fan Chunju，Gong Zhendong，et al）. 同杆双回线反序电流特点及其在T形线路测距中的应用（A faulted line selection method of parallel transmission teed line on the basis of differential current）[J].电力系统自动化（Automation of Electric Power Systems），2007，31（3）：67-71，78.

[10]戴学安（Dai Xuean）.继电保护原理的重大突破综论工频变化量继电器（A brief discussion on the protection relay based on power frequency variation principle）[J].电力系统自动化（Automation of Electric Power Systems），1995，19（1）：41-47.

[11]陈桥平，蔡泽祥，刘为雄，等（Chen Qiaoping，Cai Zexiang，Liu Weixiong，et al）.同杆线路跨线故障对选相元件的影响机理（Influence of inter-line fault on phase selection element for parallel lines on the same pole）[J]. 电力自动化设备（Electric Power Automation Equipment），2010，30（2）：95-98，112.

[12]贺家李，李永丽，董新洲，等.电力系统继电保护原理[M].4 版.北京：中国电力出版社，2010.