微电网并网最优位置选取

陈 聪，陈红坤，胡 畔，刘 欣

（武汉大学电气工程学院，武汉 430072）

由于分布式电源存在出力波动性大、控制困难、受环境因素约束大等特点，各国学者纷纷提出用“微型电网”来解决其并网问题[1-2]。微电网的核心思想在于将传统被动的负荷同小容量分布式电源相结合，使用户侧负荷成为“可控”单元，从而增强“源-网-荷”之间的互动[3]。同时在使用微型燃气轮机、燃料电池、电动汽车等可控微源的基础上，合理利用风光等能源互补的特性，能较好地解决分布式电源自身间歇性及不可控性等问题，并通过先进的控制技术实现本地可再生能源的高效利用。微电网既可看作电源也可看作负荷，其并网运行会改变传统配电网的结构与特性，因而会改变电力系统的运行方式及各项指标，如双向线路潮流、电压畸变、网络损耗率、电压稳定性等。

因此，合理选择微电网的并网位置十分重要[4]。但现有文献大多仍延用分布式电源接入电网准则，缺乏针对微电网自身特点的并网规划模式及准则[5]。文献[6]提出一种图解与遗传算法相结合的计算方法，采用图示求解大量方程，确定分布式电源的最佳容量；文献[7]采用双层优化理论，考虑电压调整约束，提出了至少准入功率的计算模型并分析了DG（distribution generator）启停对系统的影响。但上述文献均未考虑工程实际情况，忽视了地理位置与资源条件的约束。目前，我国没有明确的标准和政策用来指导和规范微电网的接入，对于各利益主体的责任分摊和收益分成也不明确。针对不同的利益主体，微电网的并网规划和运营的角度是不同的。根据我国电网实际情况，用户侧建设微电网的能力有限，本文从配电网运营商的角度考虑微电网的并网位置选取。

本文在微电网容量及电压等级已确定的前提下，根据给定的地理位置、自然资源等可行条件确定微电网并网位置候选集。从配电网运行经济性、电能质量和电网静态稳定性3 个方面建立微电网并网综合评估体系，利用模糊层次分析法对各指标进行量化与对比，确定各项指标的最佳权重系数，从工程实际的角度分析并确定微电网最佳并网位置，并采用IEEE33 节点进行算例分析。

1 微电网并网位置选取方法

1.1 微电网并网位置选取流程

本文提出的微电网接入点的选取流程如图1所示。由于资源环境、地理位置、配电网网架结构和现有国家政策的限制，实际微电网往往难以并入至配电网的任意位置。因此在微电网容量由发电商报知的前提下，首先根据实际条件确定若干可行并网位置作为后续决策候选集；在将微电网视为PQ 节点的前提下，采用前代回推法对每种方案分别进行潮流计算，剔除潮流计算不收敛的方案；选取配电网运行综合指标，并利用模糊层次分析法确定各指标的权重，确定并网位置选取的决策模型；对各备选方案进行综合量化评估，选取评分等级最高的方案作为微电网最优并网点[8]。

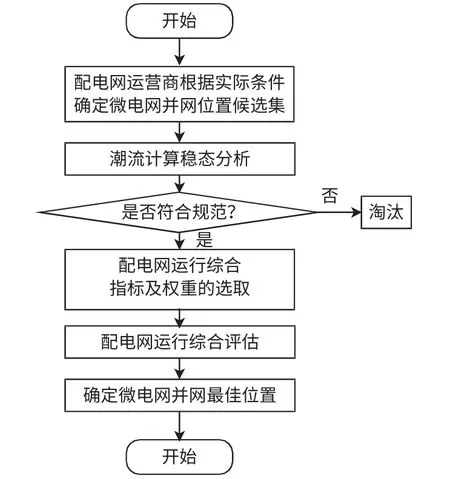
图1 微电网接入点选取流程Fig.1 Flow chart of selection for microgrid interconnection

1.2 微电网并网后配电网运行综合指标的确定

微电网并网后，配电网的各项运行指标均会发生改变，特别是在高渗透率水平下，各种微电网控制技术的运用、网络结构和运行方式对系统暂态稳定性也会产生影响[9]。由于本文分析的是微电网并入配电网以后的稳态运行情况，在此选取具代表性的网络损耗率、系统节点电压偏差、配电网静态电压稳定性指标[10]作为微电网并网后配电网的综合评判指标。其中配电网静态电压稳定性指标的计算方法如下。

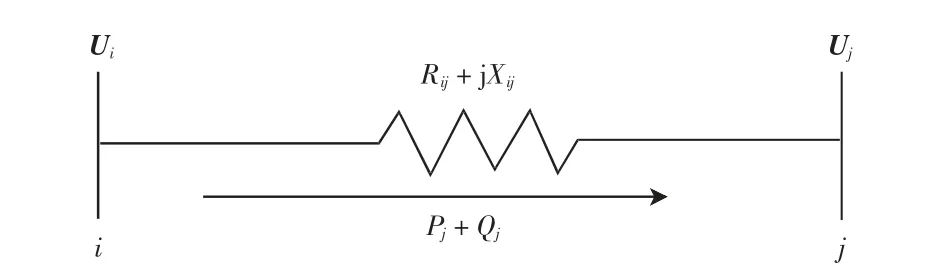
图2 简单配电网系统Fig.2 Simple distribution system

对于含有N 个节点的配电网（其中可以包含分支线路和补偿电容器），设其任意一条支路为bij，其中i 和j 分别为该支路的2 个节点，流过节点j 的负荷为Pj+Qj，支路bij阻抗Zij为Rij+jXij，如图2 所示。则

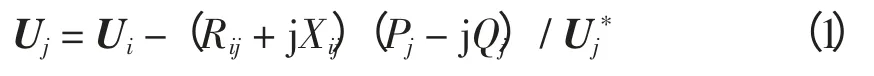
式中：Ui和Uj分别为直角坐标形式的节点i 和节点j 的电压向量；为Uj的共轭向量。

定义支路bij的第1 类电压稳定指标[11]为Lij，且

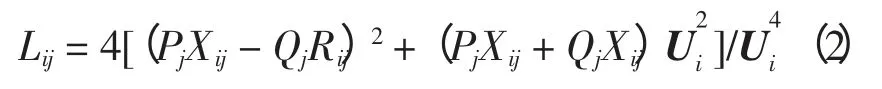
要保证配电网的电压稳定，由根判别式≥0，得Lij≤1，则整个配电网的电压稳定指标L 为

式中：Lb为整个配电网电压稳定裕度为b 的稳定指标，b=1-L。一般情况下配电网的功角δ 很小，则电压稳定指标近似值的计算公式为

式中，Sj为流过节点j 的视在功率。

1.3 配电网运行综合指标权重的选取

为了准确评估微电网并网后配电网的运行状况，需要确定各运行指标的相对权重，从而建立评估的决策模型[12]。层次分析法已在各领域得到了广泛应用，但是传统的层次分析法本身存在一定的缺陷。模糊层次分析法将传统的层次分析法与模糊数学相结合，先使用模糊数代替点值构成判断矩阵，然后求解权重向量，通过模糊数矩阵和向量计算得到模糊数综合权重，最后对其排序。该方法能有效地表达出判断的不确定性，模型的建立和求解也较为简便，传统的层次分析法可看作模糊层次分析法的一种特例。

本文采用三角模糊层次分析法来确定权重系数。三角模糊层次分析法与传统层次分析法的求解过程相类似，模糊层次分析法仍然可以按顺序分为4 个步骤：建立层次结构模型；构造出各个层次中的所有判断矩阵；层次单排序（即求取判断矩阵权重）及一致性检验；层次总排序即最终方案选择。

步骤1 建立递阶层次结构模型。

根据模糊层次分析法的基本原理，本文建立了3 个层次结构，由此来评估各指标间的关系，其层次结构如图3 所示。准则层由网络损耗、电压偏差、配电网静态电压稳定性指标3 个稳态量构成，通过对比各指标间的关系确定相对权重，进而得到指标层方案。

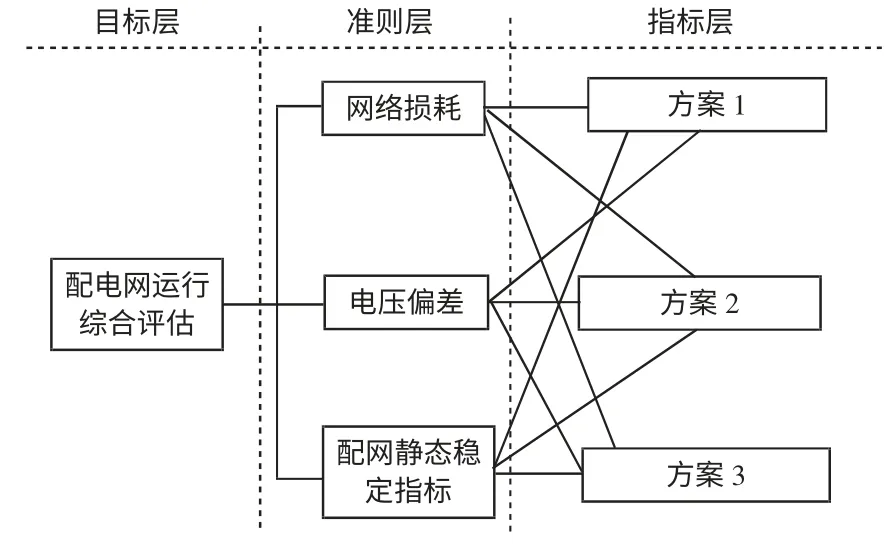
图3 配电网运行综合评估层次结构Fig.3 Hierarchy of distribution operation network composite assessment

步骤2 构造三角模糊判断矩阵。

模糊层次分析法属于主观赋权法，权重的选取主要依赖于经验丰富的工作人员和专家。首先，3 位专家利用模糊数（M1～M9）来表达他们对各指标的偏好，通过对同一层次的各个要素进行两两比较得到一组模糊数，分别为（P1，M1，U1），（P2，M2，U2）和（P3，M3，U3）。重复以上步骤，构造出的初始模糊判断矩阵如表1 所示，其中，C1为系统网络损耗率，C2为系统电压偏差，C3配电网静态电压稳定性指标。

表1 初始三角模糊判断矩阵Tab.1 Initial triangular fuzzy judgment matrix

将初始矩阵中3 位专家给出的每个模糊数按（P1+P2+P3）/3，（M1+M2+M3）/3，（U1+U2+U3）/3整合成一个模糊数，得到最终的模糊判断矩阵，如表2 所示。

表2 最终三角模糊判断矩阵Tab.2 Triangular fuzzy judgment matrix

步骤3 一致性检验。

本文采用较为简便的和法，求得判断矩阵的最大特征根为3，计算该矩阵的平均一致性指标为CR=0〈0.01，一致性检验通过。

步骤4 去模糊化处理。

各指标层关于目标的三角函数形式的综合权重依次为

要得到指标层对目标的常数形式的综合权重，需要建立可能度矩阵。根据文献[13]的方法，本文采用中立的态度，取λ=0.5，对三角模糊数形式的综合权重进行两两比较，并利用公式

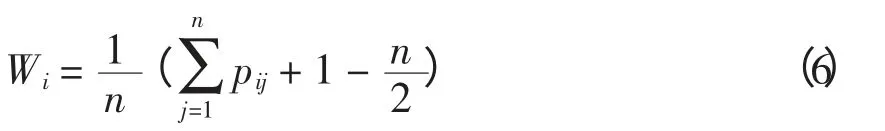
计算可能度判断矩阵P 的排序向量WT，得

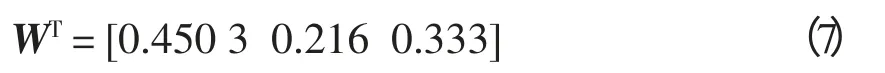
由此，系统网络损耗率、系统电压偏差、配电网静态电压稳定性指标这3 个指标占配电网运行综合指标的权重分别为：0.450 3，0.216，0.333。

根据选取的综合指标及权重，考虑配电网等式及不等式约束，本文建立的并网位置选取的决策模型为

2 算例分析

2.1 算例系统及并网位置候选集的确定

为了验证本文提出的微电网并网最优位置选取规划方案，在IEEE33 节点标准测试系统上进行仿真，并给出了微电网并网位置选取的具体步骤。IEEE33 节点标准测试系统的额定电压为12.76 kV，额定容量为10 MVA，系统总有功功率为3 715.0 kW，无功功率为2 300 kvar。在实际仿真过程中，为了保证各指标为同一数量级，对网损及总电压偏差标幺值分别乘以系数10 及0.1。微电网并网额定容量为500 kVA（功率因数为0.98）。

由于实际地理环境及自然条件约束、政策法律限制，微电网不可能接入至配电网任意位置。考虑配电网线路重载状况，微电网占地面积以及在同等网架条件下，参考文献[14]中关于分布式电源无功补偿容量优化配置策略接入点的选取。本文假定电网运营商允许在1、24、31、21 和17 这5 个节点处接入微电网，即节点1、24、31、21、17 构成了微电网并网位置的一个候选集，如图4 所示。

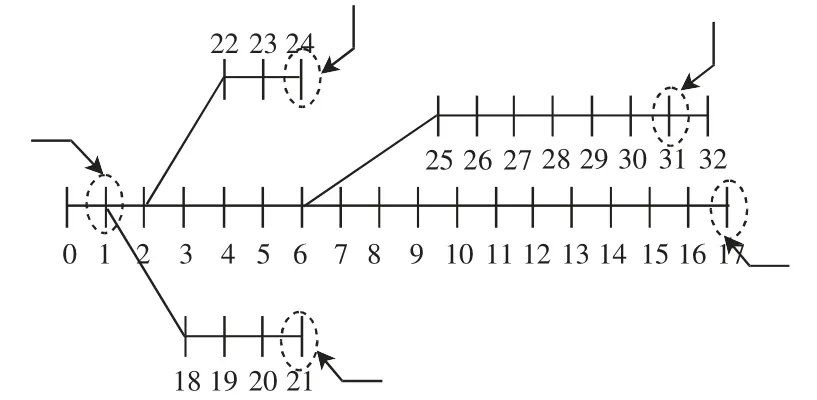
图4 微电网在IEEE 33 节点系统中的接入位置Fig.4 Interconnection location of microgrid in the IEEE 33-node system

2.2 潮流计算稳态分析

由于微电网自身的多能互补、储能配置和能量管理系统的全局控制，能维持其与配电网联络线上的功率平稳，不会存在较大的功率波动，因此在将微电网视为PQ 节点的前提下，本文采用前代回推法对配电网系统进行潮流计算。微电网分别接入候选集中的各节点后，潮流计算的收敛性和迭代次数见表3。

表3 微电网并网后系统潮流计算收敛性Tab.3 Convergence of flow calculation after microgrid accessed

微电网接入上述节点后配电网系统潮流计算结果均收敛，满足潮流稳定性要求，说明并网位置候选集中的方案均符合规范。其中微电网接入节点31 时潮流计算迭代次数最少，计算速度最快。

2.3 微电网并网后配电网运行综合评估

候选集中各方案通过潮流计算收敛性验证后，再对各方案实施后的配电网运行状况进行综合评估。综合评判指标分别为网络损耗率、系统节点电压偏差、配电网静态电压稳定性指标，评估结果分别如表4～表6 所示。

表4 微电网并网后系统网络损耗Tab.4 System losses with microgrid interconnection

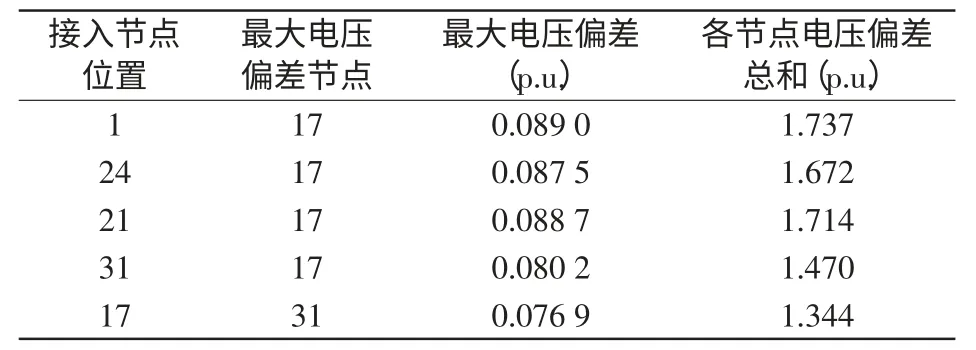
表5 微电网并网后系统电压偏差Tab.5 Voltage deviation with microgrid interconnection

表6 微电网并网后系统的静态电压稳定性指标Tab.6 Static voltage stability with microgrid interconnection

1）微电网并网后系统网损分析

分析表4 可得，微电网接入节点17 后配电网系统网损最小为185.69 kW，但与在节点31 接入的结果相差不大。由于节点31 与节点17 所在线路功率传输较高，线路负载率大，因此在负载率大的线路末端接入微电网能够减小系统网络损耗。传统分布式电源往往接入配电网首端，以增强其供电可靠性，但由上表数据看出，接入节点1 时系统网络损耗较大，长期如此运行不经济。这说明微电网的接入位置与传统分布式电源的接入位置相比有一定的区别。

2）微电网并网后系统电压偏差分析

微电网接入各节点后系统电压偏差变化规律同系统网络损耗变化规律基本一致。微电网接入节点17 之外的其他节点时出现最大电压偏差的均为节点17，且微电网接入节点17 时系统各节点电压偏差最小，这是由于节点17 位于系统最长线路的末端。当微电网接于其他节点时，无功的远距离传输显然是使节点17 的电压产生较大偏差；当微电网接于节点17 时，无功就地补偿减小了各节点电压偏差总和，改善了整个系统的电压质量。因此线路末端接入微电网能够在一定程度上提高系统各节点电压质量，尤其对于辐射状的配电网。

3）微电网并网后系统静态电压稳定性分析

微电网接入配电网的不同节点，系统的稳定裕度相差不大，但其变化规律同网损和电能质量的变化规律并不一致。因此，引入该指标是十分重要的，其独立性能够有效地指导微电网接入，微电网的并网运行在减小线路损耗和提高电能质量的同时，不容忽视其接入对配电网系统带来的负面影响。随着分布式电源及微电网在配电网系统中的渗透率不断上升，可能降低系统稳定性，在系统规划时应引起格外关注。

4）配电网运行综合评估

根据第1.3 节确定的综合评估指标权重，以及网络损耗、配电网电压偏差、静态电压稳定性指标，来决策模型，即

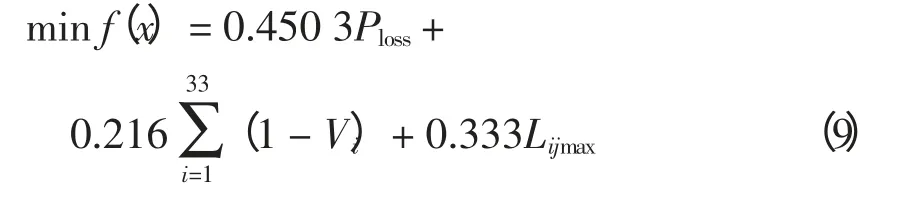
得出微电网接入各节点后的综合评分（为保证系统数量级一致，网损及总电压偏差标幺值分别乘以系数10 及0.1），如表7 所示。

表7 微电网并网后配电网运行综合评估结果Tab.7 Composite assessment of distribution with microgrid interconnection

由表7 可知，微电网接入节点17 时决策模型值最小为0.232 3。因此，微电网的最终接入位置为节点17。

3 结论

（1）本文给出了微电网并网点选取的具体步骤，选取了评估配电网运行的综合指标。

（2）利用模糊层次分析法，确定了综合指标的权重系数，建立了位置决策模型。

（3）Matlab 仿真环境下，在IEEE33 节点标准网架上进行验证。结果表明该并网位置选取方法理论充分，易于操作且工作量不大。

[1]鲁宗相，王彩霞，闵勇，等（Lu Zongxiang，Wang Caixia，Min Yong，et al）.微电网研究综述（Overview on microgrid research）[J].电力系统自动化（Automation of Electric Power Systems），2007，31（19）：100-107.

[2]姚建国，赖业宁（Yao Jianguo，Lai Yening）.智能电网的本质动因和技术需求（The essential cause and technical requirements of the smart grid）[J]. 电力系统自动化（Automation of Electric Power Systems），2010，34（2）：1-4，28.

[3]李鹏，廉超，李波涛（Li Peng，Lian Chao，Li Botao）.分布式电源并网优化配置的图解方法（A graph-based optimal solution for siting and sizing of grid-connected distributed generation）[J]. 中国电机工程学报（Proceedings of the CSEE），2009，29（4）：91-96.

[4]姚建国，杨胜春，王珂，等（Yao Jianguo，Yang Shengchun，Wang Ke，et al）.智能电网“源-网-荷”互动运行控制概念及研究框架（Concept and research framework of smart grid“source-grid-load”interactive operation control）[J].电力系统自动化（Automation of Electric Power Systems），2012，36（21）：1-6，12.

[5]Driesen J，Katiraei F.Design for distributed energy resources[J]. IEEE Power and Energy Magazine，2008，6（3）：30-40.

[6]刘琳，陶顺，肖湘宁，等（Liu Lin，Tao Shun，Xiao Xiangning，et al）.分布式发电及其对配电网网损的影响分析（Distributed generation and its impact on network loss of power system）[J].电工电能新技术（Advanced Technology of Electrical Engineering and Energy），2012，31（3）：16-19，24.

[7]徐泽水（Xu Zeshui）.三角模糊数互补判断矩阵的一种排序方法（A method for priorities of triangular fuzzy number complementary judgment matrices）[J].模糊系统与数学（Fuzzy Systems and Mathematics），2002，16（1）：47-50.

[8]Carpinelli G，Celli G，Mocci S，et al. Multiobjective programming for the optimal sizing and siting of power electronic interfaced dispersed generators[C]//IEEE Power Tech.Lausanne，Switzerland，2007：478-483.

[9]刘智昱，黄伟（Liu Zhiyu，Huang Wei）.基于稳态分析和区间层次分析法的分布式电源最佳位置确定方法（A method for optimal layout of distributed generations based on steady-state analysis and interval analytic hierarchy process）[J]. 电网技术（Power System Technology），2011，35（11）：57-61.

[10]武晓朦，刘健，毕鹏翔（Wu Xiaomeng，Liu Jian，Bi Pengxiang）. 配电网电压稳定性研究（Research on voltage stability of distribution networks）[J]. 电网技术（Power System Technology），2006，30（24）：31-35.

[11]张学松，柳悼，于尔铿，等（Zhang Xuesong，Liu Zhuo，Yu Erkeng，et al）.配电网潮流算法比较研究（A comparison on power flow calculation methods for distribution network）[J].电网技术（Power System Technology），1998，22（4）：45-49.

[12]张丽，徐玉琴，王增平，等（Zhang Li，Xu Yuqin，Wang Zengping，et al）. 包含分布式电源的配电网无功优化（Reactive power optimization for distribution system with distributed generators）[J].电工技术学报（Transactions of China Electrotechnical Society），2011，26（3）：168-174.

[13]陈庆前，余畅，章激扬，等（Chen Qingqian，Yu Chang，Zhang Jiyang，et al）.层次分析法在孤岛微网综合评价中的应用（Application of analytic hierarchy process in comprehensive evaluation of island microgrid）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2013，25（3）：133-137.

[14]黄诚亮（Huang Chengliang）.分布式电源并网优化配置（Optimal Allocation of Distributed Generation Gridconnection）[D].长沙：湖南大学电气与信息工程学院（Changsha：Institute，lectrical and Information Engineering，Hunan University），2012.