几何画板在平面解析几何教学中的应用研究

【摘 要】借助平面解析几何教学中的一系列案例，讨论几何画板在促进学生数学概念的形成、数学定理的发现与验证、数学问题解决过程中的应用。

【关键词】几何画板  平面解析几何  数学概念  数学定理  问题解决  应用

【中图分类号】 G  【文献标识码】 A

【文章编号】0450-9889（2014）12C-0156-06

几何画板是一个易学易用的数学软件，为教师和学生提供了一个探索几何图形内在关系的教学平台。它以点、线、圆为基本元素，通过对这些基本元素的变换、度量、计算和跟踪生成轨迹等方式，能构造出较为复杂的数学图形和动画效果，能根据普通方程、参数方程和极坐标方程准确地画出其对应的图形。几何画板较之其他数学软件最大的优势在于几何图形的动态化、“形”与“数”的同步化和操作的简单直观化。

笔者在平面解析几何课程教学过程中，结合几何画板的优势和五年制高职生的认知特点，有针对性地设计了大量的教学案例，并借助这些教学案例所创设的问题情境展开教学活动，充分调动了学生在操作中观察、在探索中思考、在合作中交流，不仅点燃了学生的学习热情，而且克服了传统教学中的不足，有效地促进了学习活动的开展。本文拟借助这些案例讨论几何画板在平面解析几何教学中数学概念的形成、数学定理的发现与验证、数学问题解决过程中的应用。

一、几何画板在揭示数学概念本质特征和形成过程中的应用

数学概念是对客观世界中的数量关系和空间形式的直接抽象，或是在已有数学理论上的逻辑建构，教师在进行概念教学时，应选择适当的素材，分析概念的特性，设计恰当的问题情境，使学生在经历概念发生、发展的过程中，认识理解数学概念。对于某些具有过程性特征的数学概念，如抛物线、离心率等概念，传统教学手段不易为学生提供过程性的认识材料与背景，不能很好地揭示这一类数学概念的本质特征，学生在不理解的前提下，大多对概念的认识停留在事物的表面，不能深刻理解概念的本质。几何画板可以为过程性概念提供形象、生动、直观的过程背景，有效地促进学生对数学概念的本质特征的发现与理解。

案例1：抛物线概念的理解。

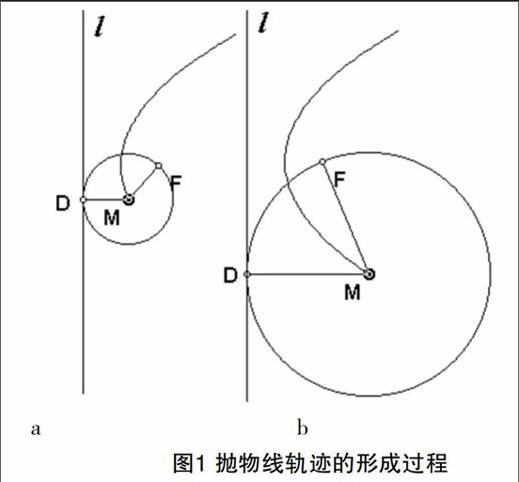
用没有伸缩性的绳索可以画出椭圆和双曲线，但却难以用传统教具流畅地画出抛物线的运动轨迹。通常情况下，教师用语言直接给出抛物线的定义，抛物线上的点所满足的条件完全由教师告知，学生难以信服与理解。而借助几何画板的动画技术，则可以流畅地表现抛物线轨迹的形成过程，有助于学生发现运动轨迹的本质特征，从而理解概念。如图1所示，点M作为动圆的圆心，在运动过程，动圆始终保持过定点F并和定直线l相切，学生通过观察动点M的运动过程和形成的运动轨迹，不仅能抽象概括出抛物线的本质属性，还能给抛物线下定义。

a                  b

图1 抛物线轨迹的形成过程

案例2：“椭圆离心率”概念的认识。

如图2所示，学生学习“椭圆离心率”时，借助几何画板中的度量、计算与跟综轨迹工具，能直观、动态地呈现焦距与长轴比值保持不变，椭圆由大不断变小，但扁平程度不变的过程，得到“离心率相同的椭圆相似或重合”的结论。如图3所示，保持椭圆长轴不变，让两个焦点距椭圆中心的距离越来越近，离心率越小，椭圆越接近圆，反之椭圆越扁平。通过几何画板的动态演示，既能直观地帮助学生认识椭圆离心率的几何意义，又能在此基础上帮助学生建立椭圆和圆之间的关系，实践证明有了上述的感性认识之后，学生不仅能够接受教材中关于离心率定义的规定，而且对其本质也有了深刻的认识，有效地提升了学生对椭圆离心率的认知水平。

a

b

图2 离心率不变、椭圆的大小改变时的对比图

a

b

图3 保持椭圆长轴不变、焦距变小时的前后对比图

二、几何画板在揭示数学定理、性质、公式发现过程中的应用

数学理论不会凭空产生，一般都会有一个实际需要或具体的问题背景，数学家们通常要经过具体的操作、演算，通过观察、分析，从中发现数学规律，形成猜想，然后从理论上给出严格的证明。平面解析几何中所涉及的数学理论，是许多数学家经过长期研究积累而形成的逻辑严密、抽象完整的理论体系，在传统教学中，学生学习这些抽象的数学理论时，往往会被忽略理论产生的背景和探索的过程。现代心理学、教育学成果揭示：学生在学习数学时，会以浓缩的形态再现人类数学发现的历程，传统教学中，由于受条件、技术、时间等诸多因素的限制，问题发现的过程均被削弱了，注重的是数学理论成果的快速学习，数学的系统性、抽象性和理论证明的逻辑性、严谨性成了课堂的主旋律，这也是学生觉得数学难学的最为主要的原因之一。几何画板可以为学生提供可进行观察、分析、思考的问题背景，让学生在丰富的感性材料中经历探索、发现数学规律过程，获得数学猜想的喜悦体验。

（一）用几何画板揭示数学定理的发现过程

案例3：发现两条直线互相垂直的充要条件。

“两直线垂直的充要条件”这一数学定理的教学，通常是教师出示定理内容，然后进行推理证明，学生对定理的内容及证明在理解与认同上总有一些困难。如图4所示，用几何画板能迅速作出两条互相垂直的直线，直接测算出这两条直线的斜率，用计算工具，求出两者之积，保持这两条直线的垂直关系不变，用鼠标任意改变这两条直线的方向，屏幕上即时呈现出两直线的斜率随两直线的方向的改变而改变，观察两直线的斜率，可以发现两直线的斜率互为负倒数关系，两直线的斜率的乘积始终为-1。学生通过观察分析，能猜想出两条直线垂直的必要条件。

aendprint

b

图4 两条直线垂直时斜率之间的关系

反过来，如图5所示，用几何画板先任意作出一条直线，然后再作出另一条与它斜率为负倒数的直线，任意改变第一条直线的方向，测算出，两直线的夹角始终为90度。学生可以猜想出两条直线垂直的充分条件。学生获取“两直线垂直的充要条件”，不再是教师直截了当地给出，而是通过操作、观察、分析猜想得来的。学生学习定理证明时，就会兴趣盎然，信心百倍。实践证明有了上述的观察猜想之后，学生不仅能够接受教材中关于两直线垂直的充要条件，而且能够通过自己的努力证明定理。

a

b

图5 两直线斜率互为负倒数、两条直线垂直

（二）用几何画板揭示数学性质的发现过程

案例4：揭示抛物线开口大小的性质。

目前的数学教材往往在问题讨论之初，就直接给出相关数学性质内容，导致学生对数学性质的感性认识的缺乏，使得学生在数学性质的接受或认同上产生困难。借助几何画板所创设的提供的感性材料和问题情境，在一定程度上可以消除这方面的影响。几何画板能通过拖动某一对象（如点、线）观察整个图形的变化来研究图形的性质。如图6所示，用鼠标沿着x轴的正方向拖动焦点F，使焦点到准线的距离p值逐渐增大，这时抛物线的开口大小也随之逐渐变大，反之，抛物线的开口变小。学生通过观察抛物线开口大小与p值大小关系的动态演示过程，不仅能自己猜想出抛物线开口大小的性质，而且加深了方程与图形对应关系的认识，同时也激发了学生进一步从理论上证明这一数学性质的兴趣。

a             b

图6 改变P值，开口大小改变

（三）用几何画板揭示数学公式的发现过程

案例5：发现数轴上有向线段的数量公式。

用几何画板在作出数轴上的有向线段AB（如图7a），测算出有向线段AB的端点A、B两点的坐标值（XB，XA），并用鼠标沿坐标轴拖动点A或点B，引导学生观察，可以猜想出数轴上有向线段的数量与终点坐标、起点坐标的关系式。如图7b所示，计算XB、XA、XB-XA 三者的值，改变A、B两点在x轴的任意位置，可以进一步验证猜想。几何画板中的度量“横坐标”工具既能直观地帮助学生发现数轴上有向线段的数量与端点坐标的关系，又能在此基础上帮助学生验证当A、B两点处于各种位置时公式的正确性，能有效地提升学生对有数轴上有向线段数量公式的认知水平。

a                                   b

图7 数轴上有向线段的数量与端点坐标的关系

（四）用几何画板揭示数学概念之间的联系

某些数学概念或对象之间既存在着联系，也存在着差异，借助几何画板的动态功能，能够很好地揭示数学概念之间所存在的联系与差异，并可以流畅地呈现由此及彼的运动变化过程，这无疑能够帮助学生深刻地认识概念的内涵与外延，概念间的联系与区别，进而发展学生的理解能力和认知水平。

案例6：用几何画板揭示椭圆、双曲线、抛物线三者之间的区别与联系。

传统教学中，学生难以理解椭圆、双曲线的第二定义，传统教具不能根据椭圆的第二定义直观的演示出轨迹图形，这也是学生心里不能完全接受和理解第二定义的原因。借助几何画板的动态演示功能不仅能够直观演示出离心率不同的椭圆轨迹图形，还可以通过改变离心率的大小，动态直观地呈现出由椭圆到抛物线、双曲线的变化过程，动态直观地揭示了椭圆、双曲线、抛物线三者之间的区别与联系。如图8所示，用几何画板的“追踪”和“轨迹”工具，能实现到定点与定直线的比为常数（可通过拖动点改变常数值）的点的轨迹的动态演示，动点M在运动时，保持到定点F的距离MF和定直线的距离MA的比值是常数0.59292时，动点M的轨迹是椭圆。如图9所示，用鼠标沿线段OS 拖动点T，可以任意改变比值e的大小。当e=1时，动点M的轨迹也随之而变为抛物线，当e>1时，动点M的轨迹也随之而变为双曲线，这样离心率的大小与椭圆、双曲线、抛物线之间的辩证关系清楚地呈现出来了，既降低了学生认知与理解上的难度，又让学生对离心率的定义和圆锥曲线的特点有了本质的认识，还能为后续学习圆锥曲线的极坐标方程服务，价值巨大。

图8 比值小于1时动点M的轨迹

大于1时，动点M的轨迹

图9 比值e不小于1时动点M的轨迹

（五）用几何画板直观、形象地揭示相关定理间的联系

数学中的某些重要定理及其相关知识，不仅需要让学生认识、理解定理的条件和结论部分，掌握定理的推理证明方法，知道定理的由来，而且还需要让学生把握这个定理与其相关定理或知识间的内在联系，从而帮助学生系统地认知数学，培养学生的数学发现能力和数学思维能力。借助几何画板其动态演示功能，可以把相关定理等知识的演变过程直观、形象地揭示出来，从而帮助学生深刻地认识相关定理之间的联系。

案例7：揭示两直线三种位置关系充要条件定理之间的区别与联系。

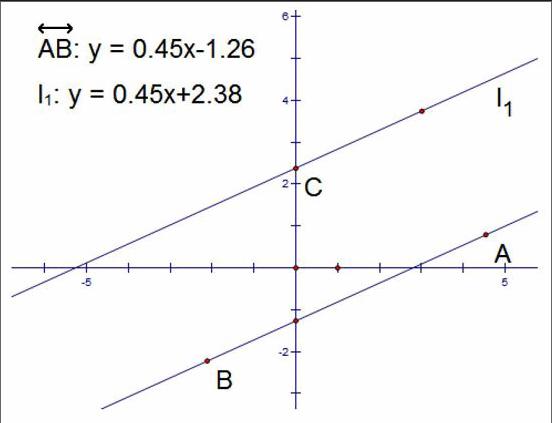
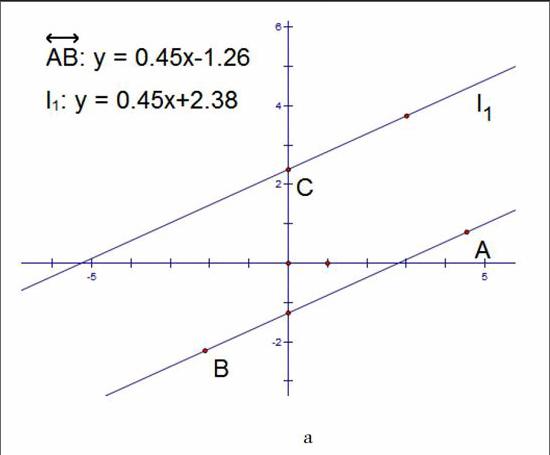
几何画板能测算出直解坐标系中直线的点斜式方程，通过拖动或旋转某一直线，可以探究观察两条直线的位置与两直线的斜率与截距之间的关系。如图10所示，直线l1可以做上下平移运动，运动过程中与直线AB平行或重合，通过引导学生观察两直线方程的斜率和在Y轴上的截距，学生能发现两条直线平行或重合的必要条件。让直线l2绕C点旋转，学生可得出两直线相交的必要条件，通过以上的两个动态演示，学生发现了两直线平行、重合、相交必要条件及之间的联系，这样进行教学不仅有益于学生发现定理内容与定理之间的联系，而且还能培养学生系统地把握和认识数学知识的能力。endprint

b

d

图10 两直线的三种位置关系与对应直线方程的显示

三、几何画板在问题解决过程中的应用

数学发展史表明，某类数学问题的解决会产生与之相关的数学理论或数学方法，譬如，微分学及求导等一系列数学理论和数学方法的产生，就是源于求运动物体的即时速度这类问题的解决，解析几何中所涉及的大部分数学理论或数学方法，都是前人在求解相应的数学问题时所得到的，尽管学生目前所遇到的数学问题不是那么深奥复杂，但对于学生来说，却是难于求解的数学问题，其中的一些问题借助几何画板不仅能帮助学生更加深刻地认识问题本身，而且还能帮助学生在解答的过程中寻找问题求解的一般方法，从而降低解决问题的难度，提高问题解决能力。

（一）借助几何画板快速呈现平面上点的运动轨迹

探求点的轨迹是平面解析几何研究的重要问题之一，一直以来都是学生难以理解和掌握的内容，传统教学中，学生只能手工画出动点轨迹的草图或在头脑中简单地想象，轨迹的精准性、完备性往往难以把握，手工画图常使学生、教师在解题思考时，考虑得不够完整全面，遗漏了动点的特殊位置以及动点运动的多种情形，从而造成轨迹的遗漏和不完整。借助几何画板，可以直观、动态地描绘出运动轨迹的形成过程，帮助学生认识轨迹的本质特征，有助于学生从中获得解决问题方法。

案例8：求分别位于两定圆上两动点连线段中点的集合。

如图11a所示，点A和点B分别是两个相离的定圆上的动点，点C为线段AB的中点，当点A和点B同时在两个圆上任意运动时，求点C的集合。如果知道了动点的运动轨迹，就有助于问题求解，借助几何画板的可以迅速画出动点C的轨迹图形，如图11b所示，原来是一个圆环（限于篇幅这里不展开求解过程）。在此基础之上可以继续探索：如果两圆相交、相切、内含时，点C的轨迹如何呢，通过拖动的方式，点C的轨迹图形能准确快速地呈现出来。求轨迹方程是解析几何教学过程中的重难点之一，学生往往不知道运动轨迹是什么图形，从而会影响问题的解答，然而借助几何画板不仅能够直观、形象地帮助学生“绘出”相应的满足条件的所有点的集合，而且在此基础上还能进一步分析、寻找问题求解的方法，达到全面地、本质地认识数学问题的目的。

a

b

图11 点C的轨迹是一个圆环

（二）借助几何画板快速呈现直线的运动轨迹

几何画板的绘图功能和动态移动功能，不仅能对点进行“追踪”显示“轨迹”，而且也能对直线或其他图形对象进行“追踪”并显示“轨迹”。能够直观、动态地呈现运动对象的轨迹图形，从而帮助学生“找到”相应的问题求解集合，在此基础上，启发学生思维，为学生提供问题求解的线索和一般方法。

案例9：求满足条件的折痕所在直线集合。

一张纸上画有半径为r的圆C，在圆C外有一定点T，且OT=b，折叠纸片，使点T刚好与圆周上某一点T′重合，这样不断进行折纸，每一种折法，都有一条直线折痕。当点T′取遍圆周上所有点时，求所有折痕所在直线的集合。按求轨迹方程的一般方法求直线集合中的点的横纵坐标x，y之间的关系式是极为困难的。如图12所示，借助几何画板的“轨迹”工具，能迅速得到所求点的集合的图形是“双曲及其外部”。进一点探讨：如果点T在圆C内时，折线的集合又是怎样的图形呢？通过拖动改变点T的位置和圆的大小，能很快能地得到所求点的集合的图形是“椭圆及其外部”，如图13所示。限于篇幅，这里略去问题的最终求解表达式求及解过程的相关叙述。借助几何画板能有效突破问题求解过程中的“画出轨迹图形”这个难点，显然这是传统教学手段无法达到的。把几何画板和问题解决有机地结合起来，可以开辟问题求解的新平台，对这个平台的使用能极大地促进学生的问题解决能力的提高，促进学生思维品质的提升，这无疑是对解析几何教学的促进。

图12 T点在圆外折痕集合

图13 T点在圆内折痕集合

综上所述，用几何画板辅助平面解析几何教学是传统教学手段的有力补充，借助其所创设的问题情境开展数学教学能够极大地促进学习活动的有效开展，但使用时要根据教学的实际需要恰当地选择，科学地设计，要以激发学生思考、提升学生的思维品质、提高教学效果为目的，不能为了用几何画板而生硬地使用，这样会适得其反。

【参考文献】

[1]邵光华.数学概念的分类、特征及其教学探讨[J].课程教材教法，2009（7）

[2]莫平.论信息技术优化高职数学课堂学习环境[J].商丘职业技术学院学报，2014（2）

[3]赵生初，杜薇薇，卢秀敏.《几何画板》在初中数学教学中的实践与探索[J].中国电化教育，2012（3）

【作者简介】莫 平（1965-   ），女，武汉人，柳州城市职业学院副教授，硕士，研究方向：高职数学教育、高职计算机教育。

（责编 王 一）endprint