具有纵向可比性的体育模型经典参数检验方法

苏 杨

1 研究目的

体育学是一门综合性的学科，兼有社会科学和自然科学的双重性质，其研究领域非常广泛。实际问题的多样性和复杂性决定了体育科研中统计学方法应用的复杂性。

近年来，计算机的普及和统计分析软件的广泛使用给建模带来了便利［1］。统计检验是体育建模中的重点环节，如何正确地运用相应的统计检验方法，是体育统计应用中的重点和难点［2］。众多检验方法相互关联，有着相似甚至相同的特征。研究者若对统计理论理解不深，对统计方法掌握不够全面，容易导致统计方法的运用生搬硬套［3］。T检验、方差分析和回归分析是统计学中的三类经典参数检验方法。本研究通过综合实例比较，探寻不同检验方法的使用条件及适用范围，提高判别效率。

2 研究方法

文献资料法，实例比较法。

3 结果与分析

3.1 基本概念

3.1.1 T检验

在体育科研和教学中，假设检验是常用的统计方法，假设检验分为参数检验和非参数检验［4］。在参数检验中较为广泛采用的是T检验。

1）单个样本T检验

单个样本T检验（one-sample t-test）是在单个样本的条件下，对此样本的均值与指定的检测值的进行比较。如检验某省18岁男生的平均身高所属的总体均数μ，是否和已知的全国同年龄同性别的身高μ0相同。

2）配对样本T检验

在体育科研和教学中，经常将研究对象设置实验组和对照组，检验这两组测试数据有无显著差异，或是对同一批研究对象进行实验前后的情况进行差异显著性检验。这两种样本数据的比较，往往样本含量小，须采用配对数据的t检验。

配对样本T检验（paired-sample t-test）是比较同一对象在两种不同条件下各种情况（如平均得分等）的均值异同。这里所说配对样本是指样本 x1，x2，……xn与 y1，y2，……ym 可以颠倒顺序。如果独立颠倒，就会改变问题的性质。

例:对8名队员进行技术训练，分别测得各人阶段训练前、后两综合成绩x数据如下：

训练前 x1：66，85，77，65，70，72，75，66；

训练后 x2：70，75，80，72，84，65，83，67。

检验两组数据差异是否显著。取p=0.05。

3）独立样本T检验

独立样本T检验（independent t-test）是两个对象在同一时间下的各种情况的均值比较。这里所说的独立样本是指样本 x1，x2，……xn与 y1，y2，……ym，可以独立颠倒顺序而不对问题产生影响的样本。

例如：调查对象是某班学生的跳高成绩，一组样本是男生的成绩，另一组样本是女生的成绩。对它们可以任意颠倒学号的顺序，而不对问题产生影响。

3.1.2 方差分析

方差分析（ANOVA）又称变异数分析，有时也称为F检验。方差分析是通过均值比较，研究某一个（one-way ANOVA）或多个因素（多指自变量）对因变量所引起的作用。

常见的单因素方差分析（one-way ANOVA）用于完全随机设计的多个样本均数间的比较，其统计推断是推断各样本所代表的各总体均数是否相等。

单因素方差分析是把总变异的离均差平方和SS及自由度分别分解为组间和组内两部分，其计算公式如下：SS组间=离均平方和/组间自由度 ；SS组内=离均平方和/组内自由度；SS总=SS组间+SS组内。

单因素方差分析：核心就是计算组间和组内离均差平方和。两组或两组以上数据，大组全部在一组就是组内，以每一组计算一均数，再进行离均平方和的计算：

SS组间=组间离均平方和，MS组间=SS组间/组数-1

SS组内=组内离均平方和，MS组内=SS组内/全部数据-组数

F值=MS组间/MS组内

注意：根据方差分析的这一结果，还不能推断四个总体均数两两之间是否相等。如果要进一步推断任两个总体均数是否相同，应作两两比较。

3.1.3 回归分析

在研究中，某个现象的发生或某种结果的得出往往与其他某个或某些因素相关，如果将存在相关的两个变量，一个作为自变量，另一个作为因变量，并将两者之间不十分确定、稳定的关系用数学方程式来表达，则可利用该方程由自变量的值来估计、预测因变量的值，这一过程称为回归分析。

近年来，随着我国体育科学化的发展，在体育科研中，应用到的统计方法很多，最常见的是回归分析，广泛地应用于体育教学、训练、管理中诸如预测、评估、控制及因素分析等多方面［5］。

3.2 实例用法比较研究

实例中数据的分析处理都是借助于SPSS20.0实现。

问题一：研究一组运动员在进行运动心理培训前后的心理测试得分有无明显差异。

在体育检测中，绝大多数情况是总体正态或近似正态，而未知原总体方差，T检验适合小样本且又可在方差未知的情形，在此我们选择独立样本T检验。此检验的假设是：

原假设H。：运动员在进行运动心理培训前后的心理测试得分无明显差异；

备选假设H1：运动员在进行运动心理培训前后的心理测试得分差异显著。

进行两个独立样本T检验后结果如下：

通过表1可以看出，t统计量的显著(双尾)概率小于0.05置信水平。所以拒绝原假设，接受H1，表明运动心理培训对提高运动员心理素质有明显作用。

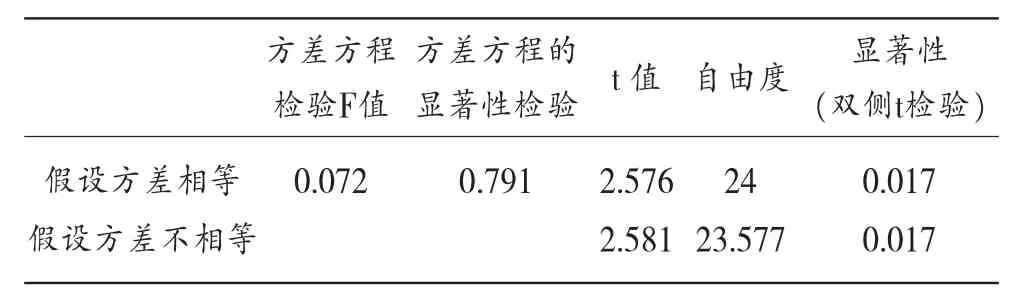
表1 双样本检验结果独立样本T检验

问题二：三种不同教学方案下学生的体育成绩是否有差异。由于教学方案这个因变量是有三个不同的水平，故选择单因素方差分析。此检验的假设是：

原假设H。：三种不同教学方案下学生的体育成绩无差异；

备选假设H1：三种不同教学方案下学生的体育成绩有显著差异。

用单因素方差分析得出的结果如下：

表2 方差分析表单因素方差分析

表3 方差分析表单因素方差分析的多重比较

由图2可知，概率P值为0.023，小于显著性水平0.05，所以接受H1，认为三种不同教学方案有明显差异。

由图3可进一步研究三种教学方案两两之间是否存在显著性差异。

对比问题一和问题二，可以看出：ANOVA和T检验都是变异数分析（analysis of variance）的其中一种。而ANOVA可以看作是T检验的扩展。T检验适用于自变量只有两个水平的均数的比较，而单因素方差分析适用于自变量有两个或两个以上的水平的均数比较。在此要说明的是，T检验的工作量很大，如果对同一组均数反复使用T检验，犯第一类错误的概率会上升。所以，一定不能在多组均数比较的时候贸然使用T检验，在多数情况下，方差分析更加合适，其优点是：将变异分类，从而能将变量的交互作用分离出来讨论研究。

问题三：在问题二的基础上，思考不同地区实施不同教学方案后学生的体育成绩是否存在差异。即需要考虑这两个自变量之间是否存在交互作用。单用T检验是不能解决这个问题的，在这个双因素实验中用方差分析来考察两个自变量的交互作用。如果交互作用不显著，则直接比较主要效果；如果交互作用显著，说明一个变量对另一个变量有影响，直接比较主效应是没有意义的，需进行单纯主要效果的比较。结果如下：

由表4知，地区类型和教学方案这两个自变量存在交互作用，需进行单纯主要效果比较。由此可以看出方差分析与T检验的关系：当样本数为2个时，方差检验结果与T检验一致。但方差可以同时检验所有自变量的均值。

表4 方差分析表双因素方差分析主体间效应的检验

问题四：研究学生体育成绩和英语成绩是否有相关关系。除了做均数比较还能做出哪些有效的统计推断。从考虑自变量和因变量的相关入手，可以利用回归分析得到自变量和因变量的线性关系。以下是采用相关分析得出的结果：

从表5中可以看出，学生体育成绩和英语成绩的相关系数为0.732，应被认为是中度相关，表明这两门学科成绩之间具有较密切的关系。从更严谨的角度，还要进行回归分析，以提高分析结果的可靠性。基于回归分析原理，我们把英语成绩当成自变量，体育成绩作为因变量，用SPSS得到回归分析，结果如下：

表5 相关性检验结果相关性分析(Correlations)

表6可看出，统计量F=11.554，显著性水平的P=0.007，说明因变量与自变量之间的线性关系明显。从表7中可以看出估计值及其检验结果，常数项等于8.721，回归系数为0.894，回归系数检验统计量t=3.399，对应的置信水平为0.007，远比常用的置信水平0.05要小，因此可认为该系数是显著的，该回归方程有统计意义：Y=8.721+0.894x。

表6 方差分析表(ANOVAb)

表7 回归系数表回归方程系数(Coefficientsa)

综上可见，回归分析与方差分析的共同点都是研究变量之间关系。不同之处在于回归分析着重在寻求变量之间近似的函数关系，方差分析着重考虑一个或一些变量对一特定变量是否有影响及影响大小。

3.3 从变异角度的比较研究

统计分析在很大程度上是分析数据的变异［6］。变异的性质和形式不同导致多种多样统计推断方法的产生。总体内个体之差异是造成抽样误差的直接原因，正因为抽样误差的存在，才需要统计描断，总体情况不同，抽徉误差的来源就不一样，因而其估计量不同，相应的统计方法也就不同。

在T检验中，分析抽样误差来源于何种变异是正确运用T检验方法的关键。 例如，对于两个正态总体 N（μ1，σ2）和N（μ2，σ2），其中参数均未知，欲推断 μ1和 μ2有无显著差异。 现从两个总体中分别抽样，得到两个样本观测值（x1，x2，……xn）与（y1，y2，……ym），抽样误差来自两个总体内部的个体差异，这就是常用的独立样本T检验。

方差分析中是将总变异按指定来源分解为若干变异之和，并以组间变异和组内变异来衡量条件因素和随机因素的影响大小，从而通过比较组间方差和组内方差以检验条件因素的作用是否显著，方差分析本身就是分解变异的一种技巧。自变量固定一个值的时候，因变量不能确定 （存在变异），这才需要回归分析。

回归分析与方差分析都是检验线性模型。回归分析中的回归系数γ2=(SSY-SSresidua)/SSY，它代表因变量y所有的变异中由自变量x造成的变异所占的比例。方差分析中F=(SSBGdfWB)/(dfGBSSWB)，F值则表示组内效应与分组效应的比值，两者都用离差平方和表示。方差分析与T检验仅仅是对均数进行比较，回归则考虑自变量和因变量之间的关系。因此，从某种角度上来说，方差分析是回归分析的特例。

4 结论与建议

综上所述，体育模型经典参数检验方法之间存在着一定形式的联系。T检验和方差分析是进行均数比较的重要手段，而回归分析在处理各种复杂变量关系的时候会有更多的解释力。鉴于体育统计学在体育科学化发展中的重要作用，提高我国广大体育科研工作者的体育统计应用水平是当务之急。无论是统计理论的学习和理解，还是统计思想和方法的应用，根据使用范围和前提假设选用正确的模型统计检验方法是提高体育统计应用水平的关键。相似的检验方法之间在应用中需要判别检验效率的高低，这些都是需进一步研究的议题。

［1］卢纹岱，朱红兵，何丽娟，等.统计软件应用的常见误区与解决途径［J］.首都体育学院学报，2005（1）.

［2］魏登云.提高体育统计应用水平的关键正确认识统计总体［J］.体育科学，1997（2）.

［3］高 亮.比较体育教学方法效果研究的假设检验问题［J］.湖北体育科技，2002（1）.

［4］郑春玲.浅谈假设检验在体育统计中的应用［J］.景德镇高专学报，2006（2）.

［5］刘厚生.回归分析方法在体育科研中的应用初探［J］.体育科学，1993（3）.

［6］魏登云.体育统计中几个重要概念［J］.安徽体育科技，2008（4）.