基于基面力的有限变形广义拟Hamilton原理

刘宗民，梁立孚，樊涛

(哈尔滨工程大学航天与建筑工程学院，黑龙江哈尔滨150001)

基于基面力的非保守系统有限变形问题是一个新兴的课题。基面力作为一种描述应力状态的新方法，较传统的应力张量表示方法简单[1]。利用基面力，各种应力张量都可以由表征位移的协变矢基的并矢来表示，可以得到弹性力学基本方程(平衡方程、边界条件、本构关系)的简洁表达式。基面力具有传统的二阶应力张量无法比拟的优越性，尤其是将基面力应用于有限变形问题，这种特点就显得十分明显。有限变形的势能原理可以和小变形情况类似的建立起来。但是，有限变形的余能原理经历了近百年，却未给出适当的表达形式。高玉臣利用基面力作为基本未知量，给出了保守系统有限变形余能原理的适当表达形式[2]。

对于非保守系统，国外以Leipholz为代表，提出广义自共轭的概念，建立了广义的Hamilton原理，给出了著名的Leipholz杆模型[3]。我国学者也作了大量工作，提出并完善了各类拟变分原理。刘殿魁提出了弹性非保守系统的一般拟变分原理[4]。梁立孚、宋海燕研究了非保守系统弹性静(动)力学两类变量的广义拟变分原理[5-6]。

对于有限变形问题，系统也常常是非保守的。文献[7]对非线性非保守系统弹性力学拟变分原理作了系统的研究。但是，由于有限变形中“裂隙函数”[8]的存在，使得对于有限变形非保守系统拟变分原理的研究变得困难。本文以基面力和位移梯度为基本未知量，“裂隙函数”自动消失了，采用变积法建立了类似于小变形情况的弹性动力学时域边值问题的有限变形非保守系统三类变量的广义拟Hamilton原理。本文研究的非保守系统专指“伴生力”系统，即作用于系统的非保守力随物体的变形而变化。

1 基本方程

按照文献[9-11]，基于基面力的有限变形时域边值问题的基本方程为平衡方程:

几何方程:

本构关系:

时域边值条件:

式中:Ti为基面力，gi为位移梯度，u为位移，ū为给定位移，mi为变形前面元单位法矢量分量，τ-0为变形前应力边界上的面力，f为单位质量物体所受的体力，R为动量矢量，V为速度矢量，ρ0为变形前的密度，VP为变形前的基容，A为单位质量的应变能，B为单位质量的余能，Sσ为给定面力的边界，Su为给定位移的边界，ū0为t0时刻位移，ū1为t1时刻位移,为对时间的导数。

2 三类变量的广义拟Hamilton原理

应用变积方法[12-13]，根据广义力和广义位移之间的对应关系，将式(1)～(6)和式(8)乘上相应的虚量，然后积分并代数相加，再对时间域积分，可得

应用Green定理:

及分部积分公式:

将式(13)和(14)代入式(12)，并按惯例在时域边界处取δu=0，经整理后可将式(12)变换为

上式可进一步表示为

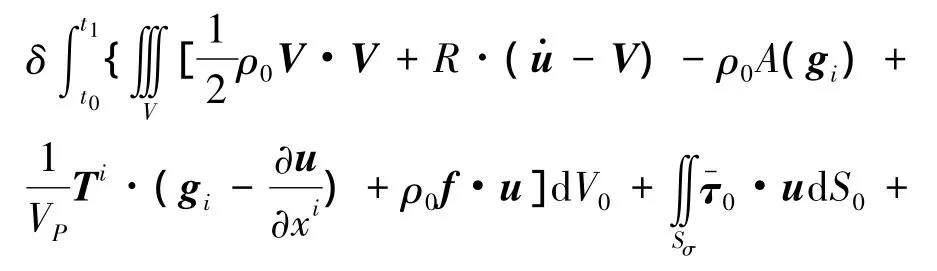
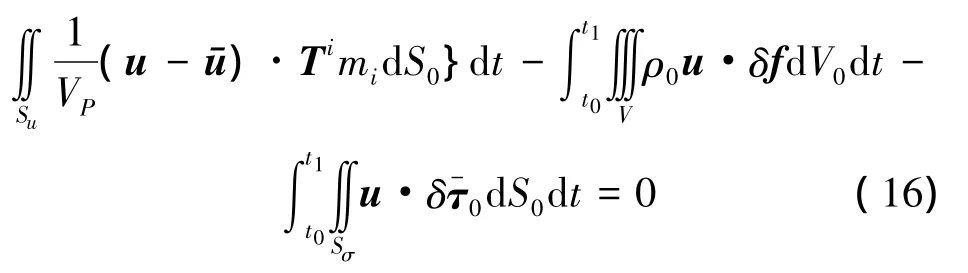
将式(16)简记为

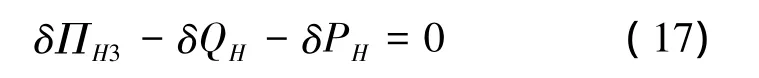
式中:

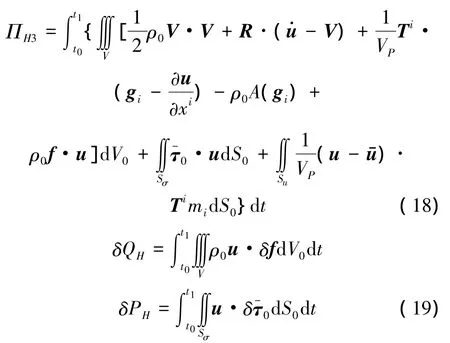
式(17)称为基于基面力的非保守系统有限变形三类变量广义拟Hamilton原理。

如果应用Green定理:

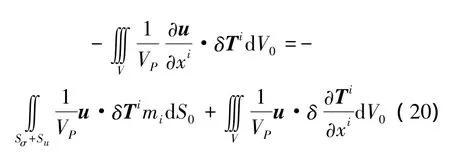
及分部积分公式:

将式(20)和(21)代入式(12)，并将式中各项改变符号，并按惯例在时域边界处取δR=0，经整理后可将式(12)变换为

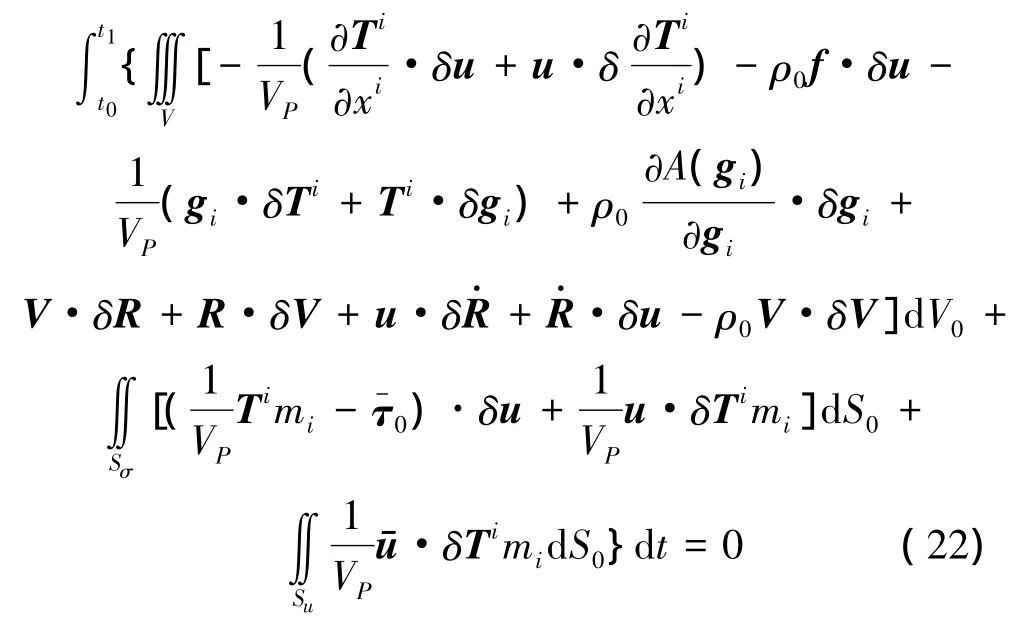
上式可进一步表示为

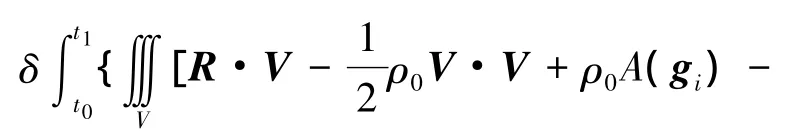
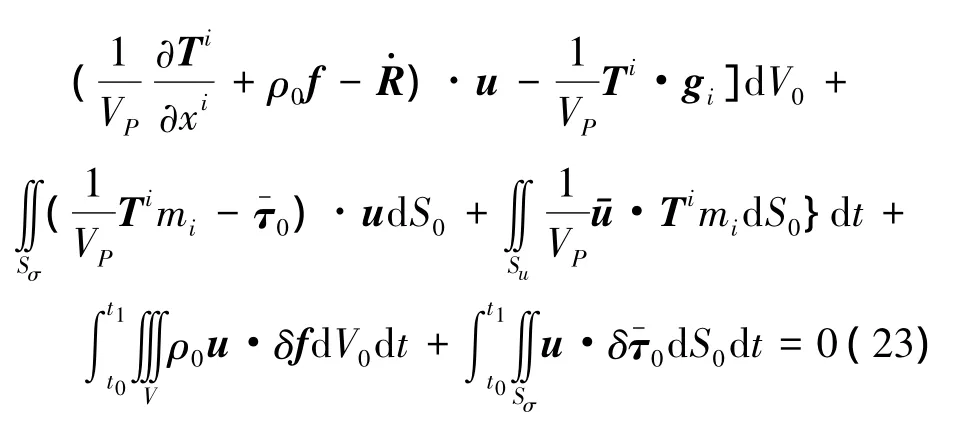
将式(23)简记为

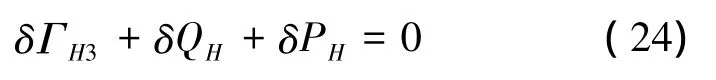
式中:

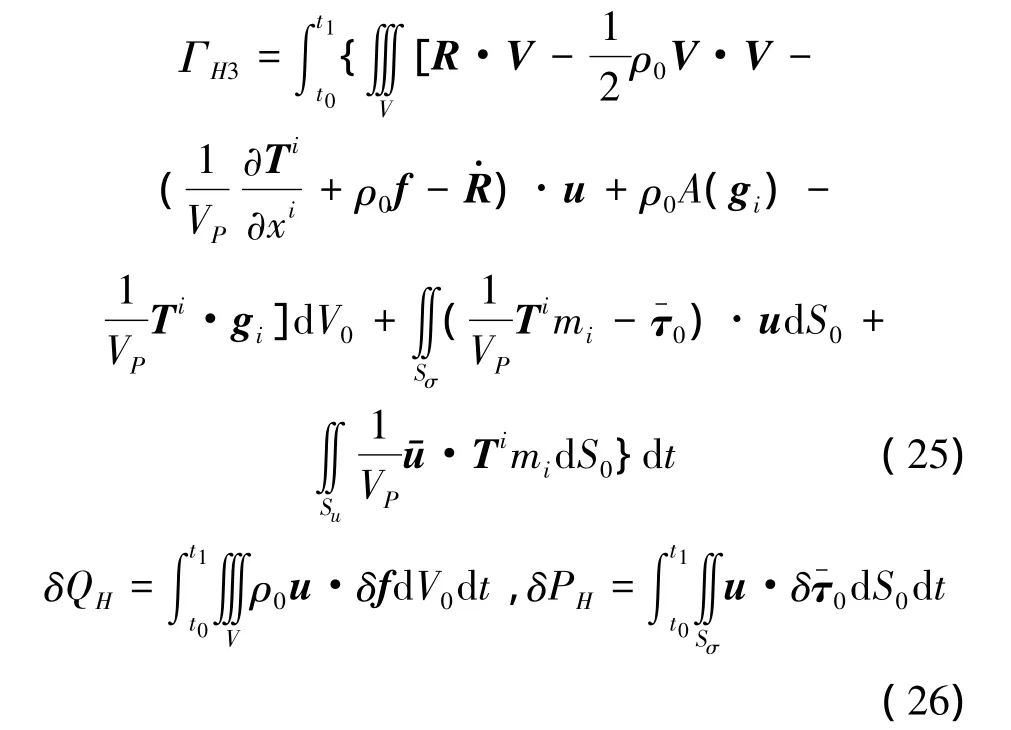
式(24)称为基于基面力的非保守系统有限变形三类变量广义拟余Hamilton原理。

由以上的推导过程可见，泛函 δΓH3+δQH+δPH=0是 δΠH3- δQH- δPH=0的对偶形式[14]。

3 正确性的验证

按照基本变量之间的对应关系，将基于基面力的有限变形广义拟Hamilton原理转化为以第二类P-K应力张量和Green应变张量为基本变量的有限变形广义拟Hamilton原理。进而证明本文建立的基于基面力的有限变形广义拟Hamilton原理的正确性。

基面力Ti与第二类P-K应力张量Σ，以及位移梯度gi与Green应变张量εG之间的对应关系可以表示为[9-10]

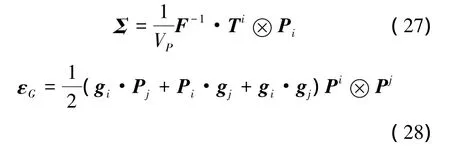
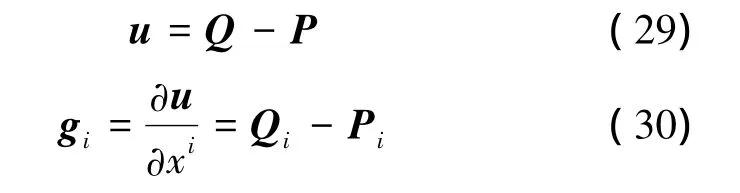
图1表示变形前与变形后的位置关系。如图1所示，位移u和位移梯度gi可以表示为式中:F为变形梯度，P和Q分别代表一点变形前和变形后的矢径，Pi和Qi分别为变形前和变形后的协变基矢，Pi和Qi分别为变形前和变形后的逆变基矢。

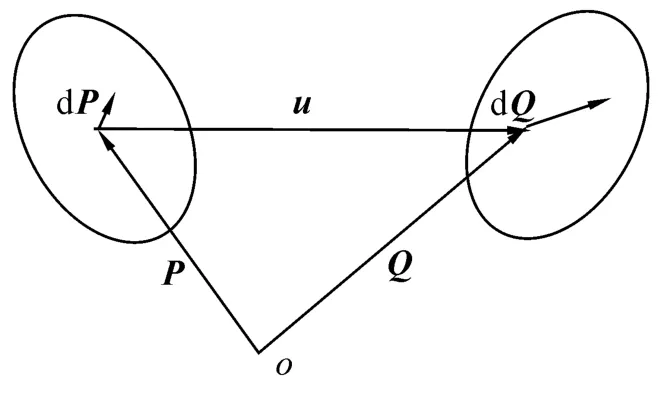
图1 位移和变形Fig.1 Displacement and deformation

将位移梯度gi表示成在标架Pj中的分量形式，可得

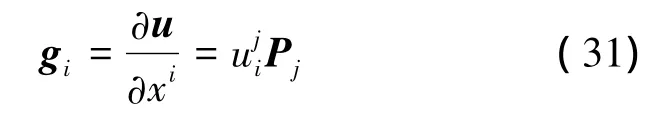
式中:tij为基面力Ti在标架Qj上的分量.

将式(29)～(31)代入式(32)，可得

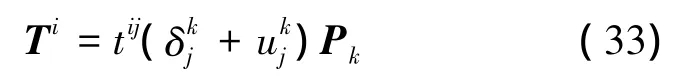
考虑式(27)、(28)、(31)和(33)，式(25)中等号右端第4项的变分式、以及等号右端第5项可以分别表示为[11，15-16]

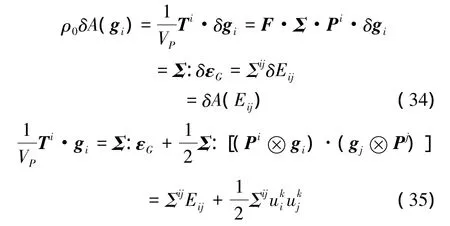
式中:Σij为第二类P-K应力张量Σ的分量，Eij为Green应变张量εG的分量.

考虑式(27)，(28)，(33)，(34)和(35)，式(17)和(24)可以分别改写为

式中:

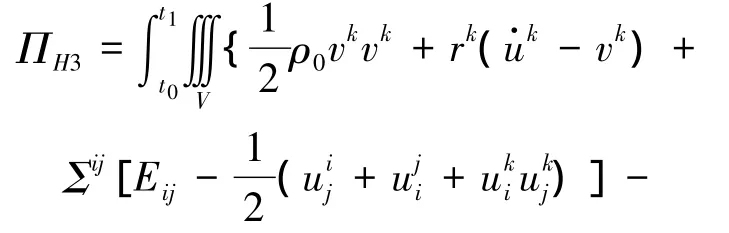
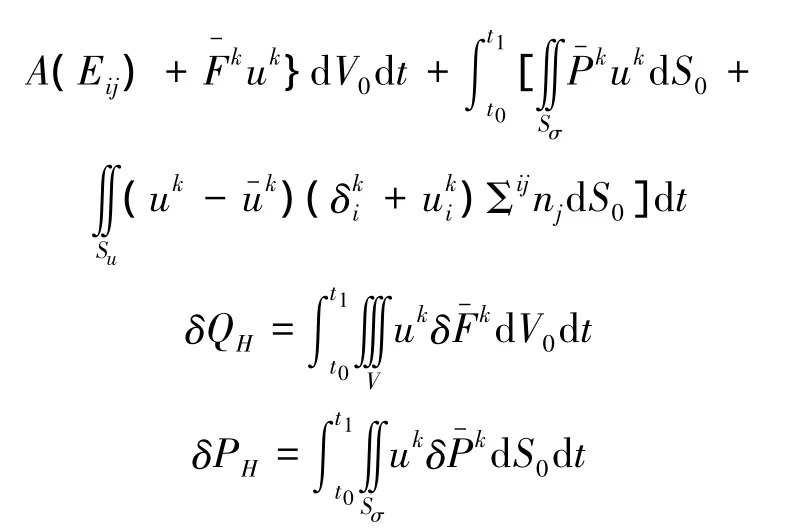
式(36)为以第二类P-K应力张量和Green应变张量为基本变量非保守系统有限变形三类变量广义拟Hamilton原理。

式中:

式(37)为以第二类P-K应力张量和Green应变张量为基本变量非保守系统有限变形三类变量广义拟余Hamilton原理。式中，vk，rk，F-k和P-k分别表示为速度分量，动量分量，体力分量和面力分量。

式(36)和(37)的表达式与文献[7]中的结果是一致的，从而证明本文建立的基于基面力的有限变形广义拟Hamilton原理的正确性。

4 结束语

以基面力和位移梯度为基本变量，应用变积法建立了有限变形非保守系统三类变量的广义拟Hamilton原理。当把基面力和位移梯度作为基本变量时，“裂隙函数”自动消失了，繁冗的公式得以简化，建立有限变形的拟变分原理就变得比较容易。本文建立的有限变形的广义拟Hamilton原理，具有和小变形情况一样的结构形式。本文的工作表明，应用基面力理论解决有限变形问题，接近于弹性小变形问题的理论和方法，这不仅使得有限变形理论和应用变得较为容易，而且对借鉴较为成熟的弹性小变形问题的理论和方法来解决有限变形的理论和应用问题提供了方便。

[1]GAO Yuchen.A new description of the stress state at a point with applications[J].Archive of Applied Mechanics，2003，73:171-183.

[2]GAO Yuchen.Complementary energy principle for large elastic deformation[J].Science in China:Series G，2006，49(3):341-356.

[3]LEIPHOLZ H.Direct variational methods and eigenvalue problems in engineering[M].Leyden:Noordhoff International Publishing，1977:207-217.

[4]刘殿魁，张其浩.弹性理论中非保守问题的一般变分原理[J].力学学报，1981(6):562-570.LIU Diankui，ZHANG Qihao.Some general variational principles for non-conservative problems in theory of elasticity[J].Acta Mechanica Sinica，1981(6):562-570.

[5]LIANG Lifu，LIU Diankui，SONG Haiyan.The generalized quasi-variational principles of non-conservative systems with two kinds of variables[J].Science in China:Series G，2005，48(5):600-613.

[6]宋海燕，梁立孚，刘殿魁.非保守弹性动力系统两类变量的广义拟变分原理及其应用[J].地震工程与工程振动，2005，25(4):24-30.SONG Haiyan，LIANG Lifu，LIU Diankui.On generalized quasi-variational principles of two-kinds of variables in nonconservative elastodynamic systems and their application[J].Journal of Earthquake Engineering and Engineering Vibration，2005，25(4):24-30.

[7]樊涛.非线性非保守系统弹性力学拟变分原理研究[D].哈尔滨:哈尔滨工程大学，2007:57-91.FAN Tao.Research on the quasi-variational principle in nonlinear non-conservative elasticity[D].Harbin:Harbin Engineering University，2007:57-91.

[8]GAO D Y，STRANG G.Geometric nonlinearity:potential energy，complementary energy and the gap function[J].Quarterly of Applied Mathematics，1989，47(3):487-504.

[9]高玉臣.固体力学基础[M].北京:中国铁道出版社，1999:14-60.

[10]金明.非线性连续介质力学教程[M].北京:清华大学出版社，北京交通大学出版社联合出版，2005:80-146.

[11]刘宗民.基于基面力的弹性大变形拟变分原理[D].哈尔滨:哈尔滨工程大学，2008:21-152.LIU Zongmin.Quasi-variational principles for large elastic deformation based on base forces[D].Harbin:Harbin Engineering University，2008:21-152.

[12]梁立孚.变分原理及其应用[M].哈尔滨:哈尔滨工程大学出版社等五社联合出版，2005:97-115.

[13]LIANG Lifu，HU Haichang.Generalized variational principles of three kinds of variables in general mechanics[J].Science in China:Series A，2001，44(6):770-776.

[14]宋海燕，梁立孚，周轶雷.一般力学广义变分原理的对偶形式[J].哈尔滨工程大学学报，2004，25(6):740-743，760.SONG Haiyan，LIANG Lifu，ZHOU Yilei.Dual form of generalized variational principles in general mechanics[J].Journal of Harbin Engineering University，2004，25(6):740-743，760.

[15]LIU Zongmin，LIANG Lifu，FAN Tao.Quasi-variational principles of large elastic deformation in non-conservative systems based on base forces theory and its application[C]//Proceedings of 2008 ASME International Mechanical Engineering Congress and Exposition.Boston，USA，2008，12:487-493.

[16]LIU Zongmin，WU Guohui，LIANG Lifu，et al.Geometric nonlinear elasto-dynamics problems solved by Variational method[C]//Proceedings of 2010 ASME International Mechanical Engineering Congress and Exposition.Vancouver，Canada，2010，8:299-305.