高旋弹丸背景涡流磁场建模与补偿
向超,卜雄洙,祁克玉,于靖
(1.南京理工大学 机械工程学院,江苏 南京210094;2.机电动态控制重点实验室,陕西 西安710065;3.上海机电工程研究所,上海201109)
地磁导航具有全天时、全天候、全地域、能耗低的优良特征,在导航定位、战场电磁信息对抗等领域展现了巨大的军事潜力[1-2]。随着地磁测量技术的发展,利用地磁测量来实现姿态测试和制导的方法已经成为弹体姿态信息获取的重要手段之一。目前地磁导航测姿主要有2种形式:1)利用地磁场在载体坐标系内的三分量和某一个已知的姿态角来求取其余姿态信息;2)利用地磁匹配的方法来确定载体位置和姿态[3]。
弹体主要由铁磁物质组成,目前所有利用地磁来进行弹体姿态测量的方法都面临背景磁场的干扰问题[4]。背景磁场的复杂性使得其成为制约弹上地磁场高精度测量的瓶颈,这导致弹体地磁导航测姿技术目前还处于辅助的地位。研究更精确、更高效的弹体背景磁场补偿方法是当前急需解决的关键问题。传统的磁补偿方法主要从磁传感器的零位误差、垂直误差、灵敏度误差入手,建立磁传感器的罗差补偿模型,先后出现了泊森(Poisson)公式补偿法、椭圆拟合补偿法、十二位置标定法、最小二乘补偿法等[5-6]。这些方法只研究了静态情况下载体所受软硬磁干扰的影响,对载体高速、高旋状态下的涡流等影响没有进行讨论,在一定程度上存在局限性,不能满足旋转弹丸高速飞行过程中的涡流干扰磁场的补偿要求。为了实现弹上高精度地磁测量,本文根据旋转弹体的材料特点和运动特征,对高旋弹体运动过程中产生的涡流磁场进行了理论研究和数学建模,通过数值仿真与半实物实验来分析涡流磁场对姿态测量精度的影响。
1 涡流磁场的产生原理与基本模型
当弹体在空间中高速运动时,弹体外壳形成闭合回路,通过其包围面积的磁通量随着地磁场在弹体坐标系三轴分量的变化而变化,在回路中产生涡旋电流,该电流反过来产生阻止这种变化的涡流感应磁场,用磁感应强度矢量Bbe表示。弹体外壳厚度要远小于与其径向尺寸,考虑到涡流现象中的集肤效应[7],在分析弹丸的涡流感应背景干扰磁场时只考虑外壳表面的涡电流现象。为了简化分析,将弹体外壳等效为一个两端封闭的空心圆柱体,以圆柱体质心为原点建立弹体坐标系o-xbybzb。
1.1 x轴方向的涡流磁场
针对弹体xb轴方向地磁分量变化,根据外壳物理特性,将其等效为法线方向为xb轴的N匝线圈串联组成的有限长直螺线管物理模型,如图1所示。

图1 xb轴涡流分析时弹体外壳的等效线圈模型Fig.1 Equivalent coil model of projectile shell in xbanalysis
图1中R为弹体径向半径,L为轴向长度。令单个等效线圈的等效电阻为Rx,根据法拉第电磁感应定律[8],可得由地磁场在xb轴上的分量Bbx的变化引起的涡流电流Iex为

根据毕奥-萨伐尔定理[9],可以得到弹体在空间运动过程中xb轴上中点处沿Bbx变化的反方向产生的涡流干扰磁感应强度为


其中,n为单位长度内等效模型线圈的匝数,其值与弹体材料的导电性能有关。exx由弹体材料的物理特性 (μr,n,Rx)和结构尺寸 (L,R)所决定,一旦材料和结构确定,exx是固定的常数。
1.2 y、z轴方向的涡流磁场
针对yb轴方向地磁分量的变化,将弹体外壳等效为法线方向为yb轴的N个矩形线圈组成。由感应电流引起的涡流磁场同理可以按xb轴方向上的分析方法得到


2 三轴耦合的涡流磁场模型
前文选取的等效线圈法线方向都与弹体坐标轴平行,使得在研究其中任一单轴向的涡流磁场时,不存在其他两轴的交叉干扰。实际中弹体外壳构成一个封闭的包裹曲面,曲面中的潜在电流回路的方向是多种多样的。
2.1 三轴涡流磁场的磁偶极子等效物理模型
对弹体外壳结构进行适合于实际情况的标准等效线圈划分,即将弹体外壳等效为N个不同法线方向的闭合回路线圈的集合。等效线圈的法线方向与3个弹体坐标轴都存在一个夹角。定义任意一个等效线圈i的法线方向ni与弹体坐标轴xb、yb、zb所成的夹角分别为βix、βiy、βiz,如2图所示。
对于单个标准等效线圈i,设其线圈平面所围面积大小为Si,其法线方向的磁感应强度的大小为弹体坐标系三轴方向的地磁场分量在其法线ni方向上的投影之和,即

设线圈的等效电阻为 Ri,令 wix=-Si·cos βix/Ri,wiy=-Si· cos βiy/Ri,wiz=-Si·cos βiz/Ri,则线圈i中由于磁通量Φi的变化而产生的感应电流为

单个线圈i法线方向等效涡流磁矩大小为mien=Si·Iie,将其投影到弹体坐标系三轴上有

式中:qiab=Si·cos βia·wib(a=x,y,z;b=x,y,z)。弹体坐标系三轴方向涡流总磁矩等于N个等效线圈所产生涡流磁矩之和,令则有


图2 任意等效线圈的示意图Fig.2 Schematic diagram of the equivalent coil

图3 涡流背景磁场磁偶极子等效模型Fig.3 Magnetic dipole model of eddy-current magnetic field
2.2 三轴涡流磁场的数学模型
设空间中有一磁矩m,以其对应的磁偶极子中心为原点,磁矩方向为z轴建立如图4所示的空间直角坐标系o-xyz与球坐标系(r,θ,φ)。
定义磁矩m所在空间的磁导率为μ,r为磁偶极子中心O到空间N(r,θ,φ)点的距离。根据坐标投影原理和磁矩空间感应强度分布理论[10],磁矩m在空间球坐标系内N点处产生的磁感应强度在坐标系o-xyz三轴方向上的分量大小BNx、BNy、BNz可表示为
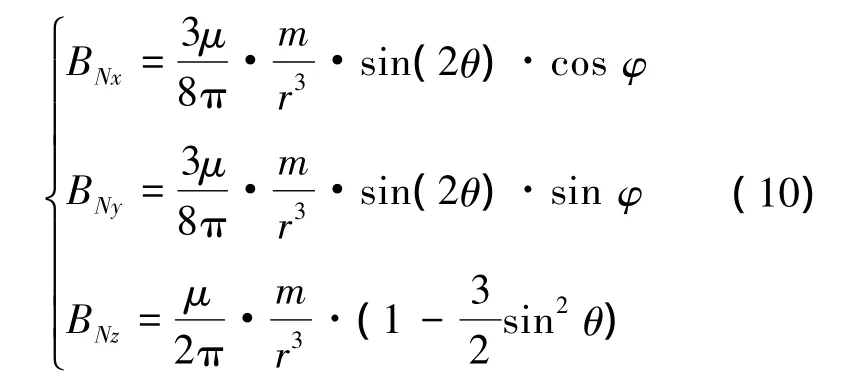
实际工作中磁传感器的安装位置不在载体坐标系原点,而是空间某点N处。利用式(9)、(10)可求得弹体坐标系内3个等效涡流磁矩在弹上安装的磁传感器三轴方向上所产生的磁感应强度。磁传感器受到的载体涡流干扰磁场的数学模型为


式中:E为涡流磁场模型的涡流参数矩阵。涡流系数的具体表达式如下:式中:rs为磁传感器安装中心到弹体坐标系原点的距离;θi、φi(i=x,y,z)是磁传感器安装中心在球坐标系中的坐标参数。从上述涡流系数的表达式可以看出,涡流系数 eij(i=x,y,z;j=x,y,z)与弹体的材料特性、尺寸、磁传感器安装位置有关,只要这些参数确定,eij就是常数。

图4 磁矩在空间某点的磁感应强度分布Fig.4 Magnetic induction intensity distribution of m in space
3 涡流磁场引起的姿态角误差分析
在弹上地磁场的测量过程中,磁传感器实际检测到的磁感应强度Bm是同时包括地磁场Bb(被测量)和涡流干扰磁场的。综合式(11)和传感器理论输出模型[11]可以得到磁传感器的真实输出模型:

式中:P、K分别为硬磁、软磁干扰矩阵;R=KE为涡流干扰矩阵。从式(12)可以看出,由于涡流干扰磁场的存在,使得磁传感器真实输出电压中出现了相应的附加干扰成分。
利用测量地磁场在弹体坐标系内三轴分量来解算姿态角时,涡流干扰磁场会引起地磁分量测量误差,进而造成姿态角的解算误差。在只考虑磁场测量误差传递的情况下,根据函数误差传递理论[12]和地磁测姿算法,利用已知的俯仰角θ求取偏航角ψ和横滚角γ的测量误差为

其中,A=BH·cos ψ·sin θ+BZ·cos θ;B=BH·sin ψ;BH表示地磁场水平强度;BZ表示地磁场垂直强度。
4 数值仿真与半实物实验研究
4.1 数值仿真分析
通过MATLAB软件仿真分析弹体涡流背景磁场对姿态角解算误差的影响。根据IGRF11模型,得到南京地区BH=33 100 nT,BZ=36 928 nT。根据某型弹丸的材料特性和前期分析工作[13],将弹丸涡流磁场参数设置如下:

按如下条件进行了仿真:θ=60°,ψ=30°;横滚角速率分别为 0、10、20、60、100、200 r/s。磁传感器噪声是均值为零、均方根为10 nT的随机白噪声。表1对不同横滚角速度时有无涡流磁场的影响情况下姿态角解算误差进行了对比。

表1 当θ作为已知量时,ψ和γ的姿态角误差Table 1 Errors of ψ and γ when θ as a known quantity
通过表1可以看出:在叠加涡流磁场的情况下,姿态角误差要远大于由于传感器噪声产生的误差。通过涡流磁场补偿后,姿态角误差满足高精度测量的要求。比较不同横滚角速度情况下的误差可以看出:随着横滚角速度的增加,涡流干扰磁场对姿态角解算精度的影响也随着增大。
4.2 半实物实验研究
利用三轴转台在三维空间模拟弹体的实际运动状态,进行半实物实验研究。半实物测量系统硬件设计选用磁传感器HMC1021/1022作为地磁敏感元件,采用C8051F320为微控制器,MAX1168为 AD芯片,AT45DB642D为外部存储芯片。系统采用数据采集回收处理的方式,利用Labview软件实现磁传感器测量数据的USB回读,并通过MATLAB软件进行涡流补偿和姿态角解算。转台实验现场如图5所示。
实验前利用系统辨识[14]的方法根据式(12)对半实物装置的硬磁、软磁、涡流干扰矩阵进行了估计,得到以下结果:

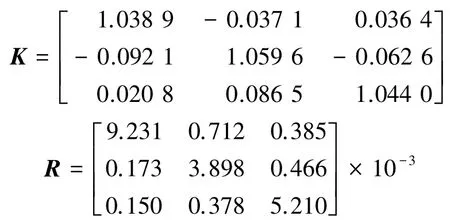
实验时将半实物装置固定在转台上,在偏航角30°±4°,俯仰角35°±10°范围内变化,横滚角正向连续变化。经消噪后的传感器输出曲线如图6所示。

图5 半实物转台实验现场Fig.5 Hardware-in-the-loop turntable experiment site

图6 消噪后磁传感器输出曲线Fig.6 Magnetic sensor output curve after de-noising
以每个时刻转台输出的姿态角(精度达0.01°)作为标准值,结合当地地磁参数(BH=33 100 nT,BZ=36 928 nT),可得到地磁分量理论检测值。图7与图8分别为测量系统只经过软硬磁补偿和经过涡流、软硬磁补偿后的地磁三分量测量误差。
对比图7和图8不难发现:经过涡流补偿后的弹体坐标系地磁场三分量的最大测量误差在0.01 A/m以内,要远小于只进行软硬磁补偿后的地磁测量误差。实验中以转台输出的俯仰角θ为已知量,利用不同补偿程度下的三轴地磁分量值进行偏航角ψ和横滚角γ的解算,结果如表2所示。

图7 只经过软硬磁补偿后地磁测量误差Fig.7 Geomagnetic measuring error after a hard and soft magnetic compensation only

图8 经过涡流、软硬磁补偿后的地磁测量误差Fig.8 Geomagnetic measuring error after eddy-current,hard and soft magnetic compensation

表2 不同补偿效果下姿态角解算误差的结果比较Table 2 Results of attitude angle calculating errors under different compensation effect
从表2的结果可以看出,利用经过涡流补偿后的地磁分量测量值进行姿态角解算的误差在±1°以内。通过对不同补偿程度下地磁分量的测量误差以及相应的姿态求解误差的比较,可以证明利用所提出的高旋弹丸背景涡流磁场模型来进行弹上地磁测量综合补偿是可行和有效的。对于高精度弹丸姿态测量的要求(姿态角误差±1°以内),必须要对背景涡流磁场进行补偿。
5 结束语
本文针对高旋弹体地磁定姿的要求,分析了载体背景涡流磁场的产生机理,建立了单轴感应下的涡流磁场模型。在此基础上通过研究弹丸涡流磁场的等效磁偶极子物理模型来建立三轴耦合涡流磁场的数学模型。通过对涡流磁场引起的姿态角测量误差进行理论分析、数值仿真和半实物实验,证明了所建涡流磁场模型用于地磁测量补偿的有效性。本文建立的涡流磁场数学模型,为进一步提高弹上地磁测量精度提供了理论依据,对高旋载体的地磁定姿技术的研究具有借鉴意义。
[1]周军,葛致磊,施桂国,等.地磁导航发展与关键技术[J].宇航学报,2008,29(5):1467-1472.ZHOU Jun,GE Zhilei,SHI Guiguo,et al.Key technique and development for geomagnetic navigation[J].Journal of Astronautics,2008,29(5):1467-1472.
[2]黄显林,李明明,卢鸿谦,等.非线性地磁/GPS/SINS组合导航方法[J].哈尔滨工程大学学报,2010,31(10):1340-1347.HUANG Xianlin,LI Mingming,LU Hongqian,et al.Nonlinear geomagnetic/GPS/SINS integrated navigation[J].Journal of Harbin Engineering University,2010,31(10):1340-1347.
[3]LIU Y J,ZHAO Y,WU F L.An improved geomagnetic matching algorithm using rotation angle search technique[J].Advanced Materials Research,2012,383:7576-7581.
[4]INAMORI T,SAKO N,NAKASUKA S.Magnetic dipole moment estimation and compensation for an accurate attitude control in nano-satellite missions[J].Acta Astronautica,2011,68(11):2038-2046.
[5]刘仁浩,王华.数字磁罗盘的全姿态罗差补偿[J].光学精密工程,2011,19(8):1867.LIU Renhao,WANG Hua.All attitude magnetic deviation compensation for digital magnetic compass[J].Optics and Precision Engineering,2011,19(8):1867.
[6]ROGERS J,COSTELLO M,HARKINS T,et al.Effective use of magnetometer feedback for smart projectile applications[J].Navigation,2011,58(3):203-219.
[7]YAMAZAKI K,FUKUSHIMA Y.Effect of eddy-current loss reduction by magnet segmentation in synchronous motors with concentrated windings[J].IEEE Transactions on Industry Applications,2011,47(2):779-788.
[8]尹国盛.大学物理(下册)[M].北京:机械工业出版社,2010:108-132.
[9]GRIFFITH J M,PAN G W.Electromagnetic fields generated by arbitrarily shaped current loops[J].IET Science,Measurement& Technology,2012,6(4):298-305.
[10]YANG Yuntao,SHI Zhiyong,GUAN Zhenzhen,et al.A magnetic disturbance compensation method based on magnetic dipole magnetic field distributing theory[J].Journal of China Ordnance,2009,5(3):185-191.
[11]LI D,WO S L,BU X Z.Twelve-position calibrating method without north using for three-axis magnetic Sensor[J].Advanced Materials Research,2012,383:5082-5087.
[12]吴石林.误差分析与数据处理[M].北京:清华大学出版社,2010:242.
[13]李玎,卜雄洙,向超,等.全磁传感器弹体定姿布阵与半实物仿真[J].南京理工大学学报:自然科学版,2010,34(5):608-612.LI Ding,BU Xiongzhu.XIANG Chao,et al.Configuration and half size hardware-in-the-loop simulation of projectile attitude determination based on magnetic sensors only[J].Journal of Nanjing University of Science and Technology:Natural Science,2010,34(5):608-612.
[14]VASUMATHI B,MOORTHI S.Improved neural network algorithms with time-varying Widrow-Hoff learning rule for harmonic estimation[J].Australian Journal of Electrical&Electronics Engineering,2012,9(4):377-385.

