舰载机着舰的动力学建模
夏桂华,董然,孟雪,朱齐丹
(哈尔滨工程大学自动化学院,黑龙江哈尔滨150001)
建立舰载机在着舰状态下的动力学模型,是完成着舰控制系统综合仿真的根本前提,该模型总体上分为两类——描述6自由度运动的非线性模型和线性扰动模型;前者能全面描述舰载机的运动,是对飞行控制系统进行试飞前评定时必然被采用的,但是运动方程的强耦合、非线性的特点导致直接进行非线性系统分析难以得出具有普遍意义的结论;相比之下,线性模型是非线性运动方程经过扰动线性化后导出的,足以描述只围绕标称状态做小幅度机动的着舰飞机对驾驶员输入以及外部流场作用的响应特性[1],利用完备的线性分析手段,可有效地研究舰载机的稳定性和操纵性,作为飞行控制系统的设计指南。美国海军的研究经验表明:在着舰控制系统的分析和完善阶段,将能描述舰载机主要特点的线性扰动模型作为地面物理仿真时使用的飞机数学模型是合适的[2-4]。
线性模型的精度很大程度上依赖于线性化方法和侧重点的选取。国内已公开的关于舰载战斗机线性建模的文献(较有代表性的如文献[5-8]),主要基于F/A-18飞机的结构及性能参数,在实现非线性建模的基础上,推导出其在风场中着舰的线性扰动模型;根据“大气扰动对着舰的主要影响是由扰流的垂直分量引起的舰载机在垂直方向上的轨迹误差”[9-10],对于考虑紊流因素的线性化过程做了简化—只考虑扰流垂直分量的作用效果,导致得出的线性模型中不含水平扰流项。
本文验证了该简化方式不合理。为此,首先研究了舰尾流场的特点,通过定性理论分析得出其水平分量对舰载机的飞行稳定性有显著影响;进而,将尾流在飞行平面内的垂直和水平分量引起的附加气动力和力矩作为干扰项引入已经推导出的无风情况下的线性模型,得到完整的舰载机纵向线性动力学模型;最后,通过舰尾流场下的舰载机线性/非线性模型的对比仿真证明结论。
1 舰载机本体特性的非线性建模
运动方程的小扰动线性化一般是在飞行器基准运动状态下完成的[11]。假设舰载机着舰阶段的基准状态为:无大气扰动情况下,舰载机在铅垂平面内以航迹角-3.5°、迎角 8.1°、航速 70 m/s 的匀速直线降落。建立舰载机非线性模型并求解基准状态是运动方程线性化的前提。为简化所研究问题的复杂性,仅针对舰载机的本体特性完成非线性建模,包括发动机推力特性和由气动布局决定的空气动力性能,不考虑飞行控制系统,并结合舰载机的运动特点和建模需要,给出下列假设[3,12]:
1)视大地为平面,重力加速度不随舰载机的位移而变化;
2)将舰载机视为在几何外形、质量分布和气动特性方面均对称的刚体,且不考虑机体弹性变形和旋转部件的影响;
3)不考虑着舰过程中由燃料消耗造成的舰载机质量和质心的变化,将发动机产生的推力当作外力;
4)处理紊流对飞行的影响时,将飞机近似为在流场中运动的一个质点。
为描述舰载机的动力学方程,本文按照通常的欧美坐标体制规范[12-13],定义的直角坐标系为:大地系Sg,牵连大地系S'g,机体坐标系Sb,气流坐标系Sa,航迹系Sk。
1.1 舰载机受力分析
1.1.1 发动机推力
载机的总推力位于机体对称平面内,在仿真条件下,合力作用线通过飞机质心,与机体纵轴夹角为0°。影响发动机推力大小的因素是飞行高度h、马赫数Ma和油门开度δp。油门杆指令δpl控制油门开度,δp对δpl的响应特性可近似为一阶惯性环节1/(1+s)。
1.1.2 空气动力
把舰载机所受空气动力在气流坐标系Sa中分解为:沿-x方向的气动阻力D,沿y方向的气动侧力C,沿-z方向的气动升力L。把空气动力对飞行器质心的力矩在机体系Sb中分解为:绕x轴的滚转力矩Lr,绕y轴的俯仰力矩M,绕z轴的偏航力矩N。计算气动力、气动力矩公式分别为

式中:S为机翼面积,m2;ρ为空气密度,kg·m-3;U为舰载机空速大小,m·s-1;b为翼展,m;CA为机翼平均气动弦长,m;CL、CD、CC分别为升力系数、阻力系数、侧力系数;Cl、Cn、Cm分别为滚转力矩系数、偏航力矩系数、俯仰力矩系数。
舰载机的气动力、气动力矩系数与迎角、侧滑角、操纵面偏角等许多因素相关,被表示为多个部分的组成,每一部分以表格形式给出,表格数据主要通过风洞试验和飞行测试获得。由于基准飞行状态下,不考虑横侧向运动和大气扰动的影响,同时将舰载机襟翼和起落架放出对气动系数的影响考虑在内。下面仅给出纵向气动系数的表示:

式中:δe为全动平尾偏角为鸭翼偏角q为俯仰角速度,rad/s;为迎角变化率,rad/s。
1.2 舰载机6自由度运动方程
完整的6自由度运动方程包含质心平动方程和绕质心转动方程两部分,每个部分又由动力学方程和运动学方程所组成。本文将方程都建立在机体坐标系下,形成“机体-机体体系”下的闭合方程组。为表达简明,定义符号(K)n表示矢量K在坐标系Sn中的坐标列阵,定义符号Lξη表示从坐标系Sη到坐标系Sξ的变换矩阵。
若将机体系的角速度矢量表示为 ωb,则有(ωb)b=[p q r]T,p和r分别代表滚转角速度和偏航角速度。舰载机质心运动动力学方程可写为
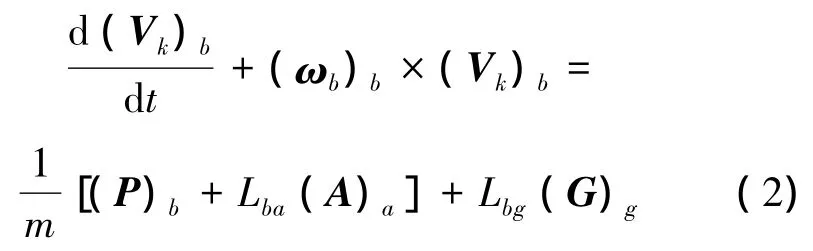
式中:vk为航速, vk( )b=[vxbvybvzb]T;P、A、G分别为舰载机所受发动机推力、空气动力和重力。
质心运动学方程把舰载机质心的位置变化率与速度相联系:航速矢量的坐标列阵由本体系变换到大地系的转换式为式(3),由航迹系变换到地面系的转换式为式(4),且将式(4)展开后可得到计算航迹角γ与航向角χ的算式。设风速vw在大地系坐标为(vw)g=[wxgwygwzg]T,可得空速U在机体系中的表达式(5),进而可得空速的大小、迎角α和侧滑角β的算式(6)。
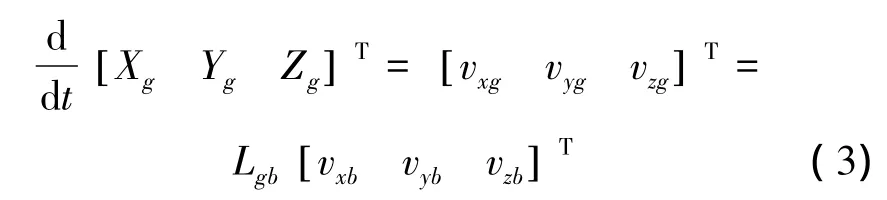

绕质心转动的动力学方程式(7)描述了刚体转动的角速度与所受合外力矩的关系,其中:H为刚体动量矩,I为刚体惯性张量,M为作用于刚体上的外力对质心力矩的合矢量。根据舰载机结构对称性可将 I()b化简为对称矩阵,元素为惯量矩Ix、Iy、Iz和惯量积Izx,kg·m2。

绕质心转动的运动学方程式(8)描述了机体系角速度和舰载机姿态角之间的关系。其中,θ为俯仰角,φ为滚转角,ψ为偏航角。

式(1)~(8)联立起来是封闭的,如图1所示,图中δr和δa分别表示方向舵偏角和副翼偏角。

图1 机体坐标系下的舰载机6自由度运动方程Fig.1 6-DOF motion equations of the carrier-based aircraft in body coordinate system
1.3 舰载机的基准状态配平
设置舰载机的操纵面偏角和油门使其运动处于平衡状态,舰载机的升力系数、阻力系数和俯仰力矩系数在配平条件下满足:式中:下标“*”表示变量在基准状态的取值,下同。

由于非线性仿真时,气动系数是在对若干个数据表格差值后再线性组合得到的,因此理论求解准确的配平点难度较大,采取迭代计算的方法,求出不同程度满足式(9)的初始输入值。表1给出3组实现近似配平数据,精度依次提高。
第3组初始输入使舰载机维持基准状态附近稳定飞行的时间最长,各项性能指标在仿真开始后15 s内的误差限制在2%以内,随后响应迅速发散,如图2所示。造成舰载机难以持久稳定飞行的根源是其本体特性的俯仰静不稳定性,在仿真中表现为与平衡状态存在微弱偏离的初始输入会使误差随着时间的积累,最终导致响应发散。有关舰载机着舰状态的纵向静不稳定性的详细验证和分析可参阅文献[13-14]。此外,3组近似配平点均在小扰动线性化范围内,因此由它们导出的线性模型将相差甚微。

表1 舰载机的近似配平数据Table 1 Approximate trim data of the carrier-based aircraft

图2 舰载机在第3组近似配平输入下的时域响应Fig.2 Time-history response of the carrier-based aircraft under the third approximate trim values
2 舰载机着舰纵向线性建模
2.1 平静大气下纵向运动方程的线性化
2.1.1 纵向力和力矩的线性化
基于小扰动线性化的基本原理和方法[12,15]及研究对象的发动机推力特性,可将推力的扰动表示为
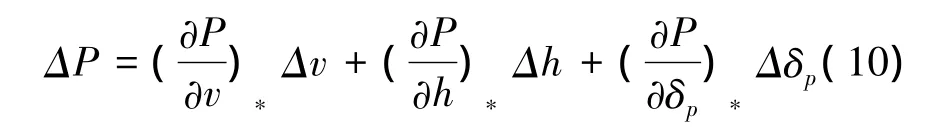
由于着舰阶段舰载机的高度变化不大且速度基本恒定,因此空气密度ρ变化很小,音速变化很小,这样马赫数基本不变(约为0.2Ma),因此空速(或航速)v对推力的影响可以忽略;此外,虽然舰载机的高度变化对其发动机推力确有影响,但经过后续的线性化处理,该影响将变得很微弱,亦可以忽略。这样,在舰载机着舰过程中,发动机推力的变化仅与油门开度相关。
高度的变化通过改变空气密度间接影响气动力和气动力矩,它们对高度的偏导数表示为

由标准大气计算公式可得[11]

指定基准高度和空气密度后,可得(∂ρ/∂h)*;此外,由式(10)可知 (∂M/∂h)*为 0。
根据前面提到的气动力、力矩计算公式和式(1),可写出气动阻力的偏量表达式为

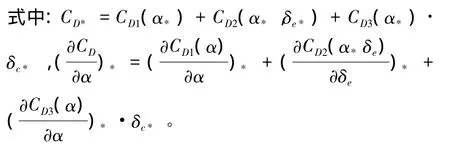
将式(14)中的“D”换为“L”,即为气动升力的扰动表达式形式:

同理,得到俯仰力矩的扰动形式:


2.1.2 纵向运动方程的线性化
基准运动状态下,舰载机横侧向通道的物理量均为零,据此可将线性化后的非线性运动方程中只包含纵向通道变量的等式组成纵向小扰动方程组,它又分为2类:一类为耦合方程组(19),另一类为解耦后的方程(20)[12]:

式(19)的前两式分别由质心动力学方程在航迹系中的表达式(21)的第1、3式线性化而来;后两式分别由式(7)展开后的第2式和式(3)线性化而来。式(20)的前两式分别由式(3)、式(8)的第3式线性化而来,第3个等式则根据无风情况下铅垂平面内对称飞行的恒等关系[13]。线性方程中各物理量的单位:力为N,舵面偏转角及油门开度为(°),其他角度和角速度的单位均为弧度制。

将式(20)代入式(19)中进行化简;为使结果便于表示,引入微分算子符号“K”并定义如下所示的稳定性和控制导数,则推得式(22);再将式(22)的第2式代入第3式,化简整理得到以状态空间方程(23)、(24)描述的舰载机纵向小扰动模型,式中Δnz为过载扰动,表示升力扰动与重力之比。



2.1.3 确定状态空间方程的参数
确定状态矩阵中的元素需要先求出气动力和力矩的偏导数,包括气动系数的基准值和在基准点处的导数值。气动系数的基准值可通过气动数据表格在基准状态处插值获得,结果列在表2中。
对式(1),求气动系数偏导数的步骤为:先将系数分量的表格数据做多项式拟合;然后求拟合多项式在基准点处的导数值;最后根据式(14)、(16)和(18)得到结果。要求拟合曲线在基准点及其附近的值与表格数据的误差尽可能小且过渡平滑,详细的处理结果见表3。将求出的稳定性和控制导数代入式(23)、(24),即得描述舰载机在平静大气下着舰的纵向模型(25)、(26)。

表2 气动系数在基准状态的值Table 2 Values of aerodynamic force and moment coefficients at trim condition

表3 气动系数分量在基准状态的导数值Table 3 Derivatives of aerodynamic coefficient components at trim condition


2.1.4 线性模型对控制指令响应的精度验证
验证线性扰动模型对非线性模型的近似精度,具体方法是:在相同的偏差指令输入下,将非线性模型的输出相对其基准状态的偏离量同线性扰动模型的对应项相比较。鉴于舰载机本体特性的静不稳定性和小扰动方法的局限性,设定的2组仿真条件为:仿真时长6 s,在2 s时刻向升降舵引入半阶跃信号指令;仿真时长8 s,在2 s时刻向油门加入单位阶跃信号。对比结果如图3、4所示。
仿真结果表明,线性模型反映了非线性模型的不稳定性,且两类模型的对应项输出在变化趋势和幅度上基本吻合,特别是在指令加入后约4 s内,之后线性系统的误差不断变大,主要原因是线性化的精度只在基准状态附近有保证。

图3 非线性和线性模型对升降舵阶跃指令的仿真结果对比Fig.3 Comparisons of the simulated linear and nonlinear model responses to the elevator step signal command

图4 非线性和线性模型对油门阶跃指令的仿真结果对比Fig.4 Comparisons of the simulated linear and nonlinear model responses to the throttle step signal command
2.2 非平静大气下舰载机纵向运动方程的线性化
2.2.1 理论分析
舰尾气流场是造成着舰偏差的主要因素之一,集中于着舰阶段的最后0.5英里(约846 m)对飞行产生影响[10];军标 MIL-HDBK-1797将其分成 4个部分:海面自由大气紊流分量、舰尾流稳态分量、舰尾流周期性分量和随机分量[16]。若设甲板风为利于着舰的情况—大小27 kn(约14 m/s),方向大致沿航母斜角甲板中线[10],则结合军标对舰尾流模型的规定和本文的仿真假设,得到作用在舰载机上的尾流场的时域仿真结果,如图5所示。
通过仿真舰尾流的过程发现:甲板风越大,尾流场强度越大,其位于舰载机垂直对称面内的分量随舰机距离的减小呈现变大的趋势,且水平分量的强度明显大于垂直分量。据此,可将影响舰载机纵向运动的舰尾紊流视为垂直和水平方向上连续分布的强度各异的突风,尝试把由突风带来的附加力和力矩作为干扰项引入已经导出的平静大气下的舰载机线性动力学模型。

图5 舰尾流场时域仿真Fig.5 Time-history simulation of ship burble
设垂直方向存在下洗流(wzg>0),它在短时间内对飞行的影响如图6所示。舰载机的航迹倾角变大且有式(27)成立,式中惯性迎角αd表示航速矢量与机体系轴xb的夹角,迎角和空速的变化过程难以直观判断。由式(27)可得式(28)。

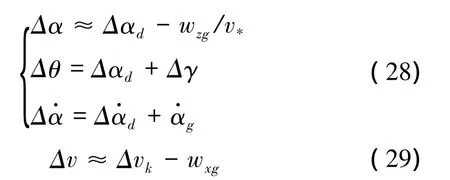
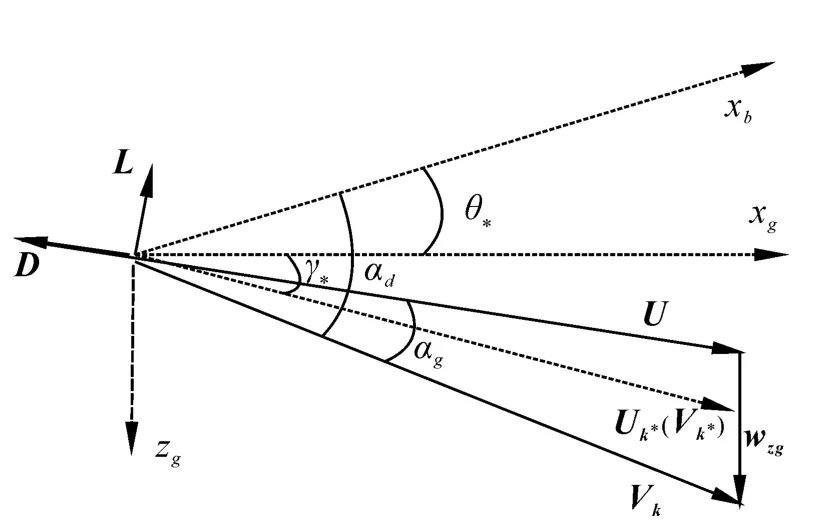
图6 垂直突风对飞行的影响Fig.6 Influence of vertical gust on flight
若紊流方向与进场方向平行(wxg>0),则在气动效果上相当于舰载机空速降低,有式(29)满足,式中的Δv代表空速扰动,Δvk代表航速扰动。联系图5的仿真结果和舰载机气动力、力矩计算公式,可以估算出舰载机升力和阻力的变化幅度有几千甚至上万牛顿,对于控制精度要求很高的着舰过程,这是值得重视的要素。因此在线性动力学建模时只考虑流场的垂直分量的作用效果或者认为水平分量和垂直分量一起只对(惯性)迎角产生突出影响的做法都欠妥。
综上分析,将平静大气下的线性模型“改造”为风场中动力学模型的方法是:将式(28)第1式代入式(19),除了速度微分项不变外,式(19)的Δv均由式(29)取代;用式(28)第2式取代式(20)第3式;采用与前面推导线性模型完全类似的做法,即得描述舰载机在舰尾流场中着舰的纵向动力学模型(30)~(33)。


2.2.2 线性模型对紊流响应的精度验证
验证风场下的线性扰动模型对非线性模型的近似程度。根据前面设置仿真条件的经验,并考虑舰尾流场的特点,截取图5在12~16 s的舰尾流前向分量和垂直分量的仿真数据作为模型扰动输入,得到3组对比结果,如图7~9所示。
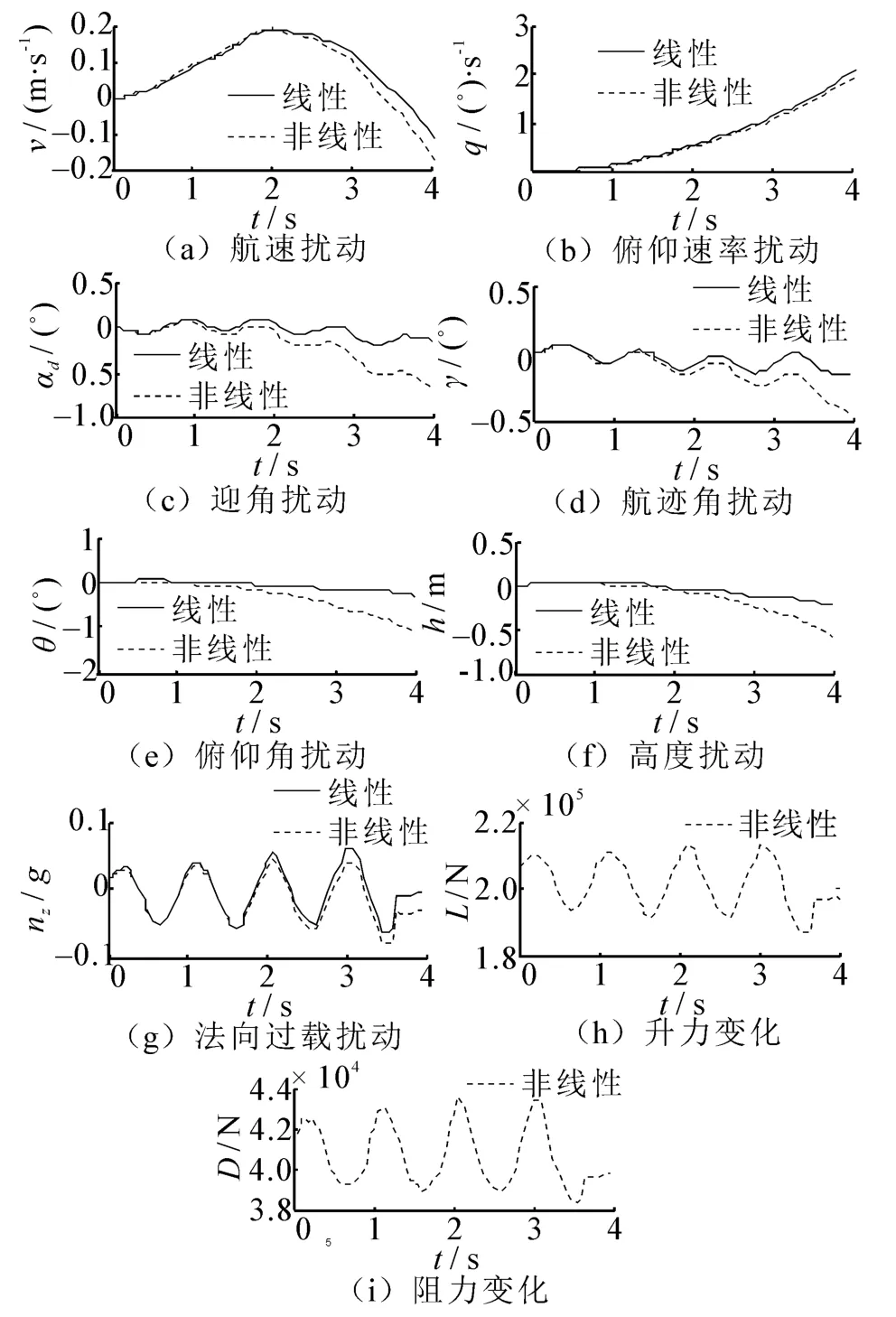
图7 非线性和线性模型对舰尾流垂直分量的响应Fig.7 Simulated linear and nonlinear model responses to the vertical component of ship burble
图7表明,加入扰流垂直分量后的2.5 s内,除航速以外,线性模型同非线性模型的各对应输出响应均很接近。研究线性模型在航速变化方面误差较大的原因发现,这是本文针对舰载机着舰动力学所采取的线性化方法的固有缺陷。一个简便的验证方案是:数值仿真环境下,用脉宽为0.5 s的单位脉冲信号代表稳态垂直扰流(下洗风),在1 s时加入2类模型中;结果显示,脉冲存在时,2类模型唯独在航速响应上呈现出完全相反的趋势,如图10(a)所示;对于非线性模型,依据图6,分析航速方向上的受力,仿真结果如图10(b)所示,并由此可见突风的存在确实会引起航速减小,如图10(a)中虚线所示;而对于线性模型,由式(30)可得

式中:除 xvΔvk外的各项均为正;虽然xv< 0,但xv数量级太小,因此线性模型的惯性速度为正。
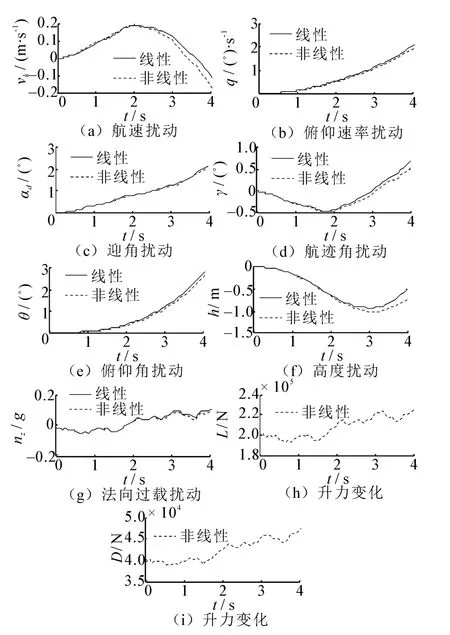
图8 非线性和线性模型对舰尾流水平分量的响应Fig.8 Simulated linear and nonlinear model responses to the horizontal component of ship burble
即便如此,图9表明,补充舰尾流水平分量后,该“缺陷”明显减弱,至少在受扰后的1.5 s,线性模型各项输出指标的误差较小。综合舰载机本体特性的静不稳定性并结合前面的仿真结果可知,本文的小扰动线性化过程是合理的,线性模型符合在着舰控制系统仿真中使用的飞机动力学模型的要求。此外,从很大程度上,图7中的实线课被视为仅考虑了舰尾流垂直分量影响的线性动力学模型在完整舰尾流作用下的响应情况,这样与图9的虚线对比后可知:对舰载机着舰的纵向线性建模必须重视紊流在水平方向上的分量。


图9 非线性和线性模型对舰尾流的响应Fig.9 Simulated linear and nonlinear model responses to ship burble

图10 线性模型的缺陷验证Fig.10 Verification on the flaw of linear model
3 结束语
本文在建立舰载机6自由度非线性模型的基础上,应用小扰动理论,完成了对舰载机着舰纵向动力学的线性建模。数值仿真环境下,动力学模型对控制指令和舰尾流场的响应表明,在基准状态附近,线性模型相对非线性模型具有较高精度,可作为在着舰仿真中使用的飞机动力学模型。
理论分析以及线性、非线性对比仿真都证明,影响着舰过程的紊流水平分量会对舰载机稳定性产生显著干扰,对线性模型的精度起决定作用,因此是舰载机纵向线性建模所必须考虑的因素。
[1]DURAND T S,WASICKO R J.Factors influencing glide path control in carrier landing[J].Journal of Aircraft,1967,4(2):146-158.
[2]DURAND T S,WASICKO R J.An analysis of carrier landing[C]//Aircraft Design and Technology Meeting.Los Angeles,1965.
[3]DAVIES W D T,NOURY R.AN/SPN-42 automatic carrier landing system[C]//Proceedings of the First Annual Advanced Control Conference.Lafayette,USA,1974:99-110.
[4]RUDOWSKY T,COOK S,HYNES M,et al.Review of the carrier approach criteria for carrier-based aircraft.NAWCADPAX/TR-2002/71[R].[S.l.]:Naval Air Warfare Center Aircraft Division,2002.
[5]彭兢.舰载舰载机进舰着舰的自动引导和控制研究[D].北京:北京航空航天大学,2001:167-170.PENG Jing.Research on the automatic guide and control of a carrier-based airplane approach and landing[D].Beijing:Beihang University,2001:167-170.
[6]邓娟.舰载舰载机自动着舰纵向控制系统设计的理论与仿真研究[D].上海:复旦大学,2010:30-53.DENG Juan.Theory and simulation for the design of longitudinal automatic carrier landing system[D].Shanghai:Fudan University,2010:30-53.
[7]刘冰.基于LQG/LTR方法的舰载舰载机自动着舰系统设计的理论及仿真研究[D].上海:复旦大学,2010:25-41.LIU Bing.Research on theory and simulation for the design of automatic carrier landing system based on LQG/LTR[D].Shanghai:Fudan University,2010:25-41.
[8]吴鑫.舰载机自动着舰控制系统设计与研究[D].哈尔滨:哈尔滨工程大学,2009:8-20.WU Xin.Design and simulation for the automatic carrier landing control system[D].Harbin:Harbin Engineering U-niversity,2009:8-20.
[9]张明廉,徐军.舰载舰载机自动着舰系统的研究[J].北京航空航天大学学报,1994,20(4):386-391.ZHANG Minglian,XU Jun.Research on the automatic carrier landing system[J].Journal of Beijing University of Aeronautics and Astronautics,1994,20(4):386-391.
[10]SCHUST A P,YOUNG P N,SIMPSON W R.Automatic carrier landing system(ACLS)categoryⅢcertification manual.AD-A1181817[R].[S.l.]:ARINC Research Corporation,1982.
[11]肖业伦.飞行器运动方程[M].北京:航空工业出版社,1987:12-35,62-81,90-103.
[12]方振平,陈万春,张曙光.航空飞行器飞行动力学[M].北京:北京航空航天大学出版社,2012:16-31,174-214.
[13]ROBERT C N.Fligt stability and automatic control[M].2nd ed.New York:McGraw-Hill,1997:42-53.
[14]董然.ACLS纵向内回路控制系统研究[D].哈尔滨:哈尔滨工程大学,2013:17-21.DONG Ran.Research on the longitudinal inner loop configuration in ACLS[D].Harbin:Harbin Engineering University,2013:17-21.
[15]钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2011:158-162,179-184.
[16]MIL-HDBK-1797,Department of defense interface standard,flying qualities of piloted aircraft[S].[S.l.]:Department of Defense,1997.

