混合距离算法在蒸汽发生器优化设计中的应用

阎昌琪，陈磊，王建军

(哈尔滨工程大学核安全与仿真技术国防重点学科实验室，黑龙江哈尔滨150001)

多目标优化问题起源于许多实际复杂系统的设计、建模和规划。几乎每个重要的现实生活中的决策，都需要进行多目标优化[1]。

20世纪80年代中期，进化算法作为求解多目标优化问题的新方法受到了广泛关注，并逐渐涌现出很多种进化多目标优化算法，其中一些已成功应用到工程实践。OSYCZKA和KUNDU基于当前个体与非支配解之间的距离，建立适应值分配机制，于1995年提出了距离方法[2]，并于1996年对其进行了适当改进[3]。但是，如何提高该算法的收敛精度、非支配解的连续性和非支配解的宽展度，一直没有得到很好的解决。为此，采用复合形算法中的深度搜索策略[4]和免疫克隆算法中的高频变异策略[1]对其进行改进，提出一种混合距离算法，试图提高非支配解质量。

蒸汽发生器是核动力系统中大型设备之一。在满足其设计要求的条件下，优化其重量、体积和其他设计指标，能够降低其制造、运输和安装过程中的成本和难度。但是，以往的蒸汽发生器优化设计，多针对单个目标，即减小其重量[5-8]。这种方法的主要弊端是在重量达到最优时，其他设计指标可能被恶化。为此，采用混合距离算法开展了蒸汽发生器多目标优化的研究，试图使优化结果更加合理。

1 多目标优化问题

最优化是在多种可能的选择多目标优化问题中，搜索对于某些目标的最优解。如果存在的目标超过一个，并需要同时考虑，这个问题就是多目标优化问题[9]。

为不失一般性，最小化多目标问题可表述为

在有多个目标时，由于可能存在目标之间的无法比较和冲突的现象，不一定存在使得所有目标同时达到最优的解。甚至有可能一个解使某个目标达到最优，但使其他目标达到最差。因此，在有多个目标时，通常存在一些无法简单进行相互比较的解，这些解就是非支配解[9]。

假设有一个q维解空间Z，对于其上一点z＇，当且仅当不存在其他点z，使得对于最小化情况有:

这样的z'称为非支配解。

2 混合距离方法

2.1 传统距离方法

传统距离方法采用非支配解潜在值的概念，确定个体适应值，用以计算交配概率。对于新产生的个体，基于其与所有非支配解之间的最短距离，计算其适应值;如果新解为非支配解，则还需对其赋予潜在值。

新产生的个体应属于下列3种类型之一:

1)是一个非支配解，支配一些当前的非支配解;

2)是一个非支配解，但不支配任何当前的非支配解;

3)不是非支配解，至少被一个当前的非支配解支配。

对于第1种情况，新解的潜在值是当前最大潜在值与最短距离之和;另外，采用其更新当前非支配解集。对于第2种情况，新解的潜在值是与其距离最短的非支配解的潜在值加上最短距离;另外，将该解加入当前非支配解集中。对于第3种情况，新解的适应值由与它最近的非支配解的潜在值减去最小距离来确定。

2.2 约束处理

对于一般性的优化问题，需处理各种各样的约束函数。OSYCZKA和KUNDU采用外部罚函数(式(3))，将有约束问题转化为无约束问题[9]:

式中:x为优化变量，fk(x)为第k个目标函数下的函数值，hi(x)为等式约束，gi(x)为不等式约束。当个体满足不等式约束条件时，Gi=0;当个体不满足不等式约束条件时，Gi=1。r为正乘子，控制惩罚项幅度。

2.3 算法初始化

在产生初始种群后，选出其中的非支配个体，并赋予相同的潜在值。对于余下的个体，依据其与最近非支配解的距离，计算其适应值。为确保选择过程的正常操作，当个体的适应值小于0时，则将其重置为0。

2.4 复合形深度搜索策略

遗传算法具有很强的全局搜索能力，即使在所定义的适应性函数是不连续、非规则的或有噪声的情况下，它也能以很大的概率找到全局最优解区域。但是，在遗传进化后期，往往会出现群体的平均适应度已接近最佳个体适应度，使个体的竞争力减弱，最佳个体和其他大多数个体几乎有相同的选择机会，从而使有目标优化趋于无目标的随机漫游过程。

为克服遗传算法局部搜索能力不强的缺点，本文在传统距离方法的基础上引入复合形算法中的深度搜索策略，当产生的子代个体为满足约束条件的非支配解时，则沿父代个体指向子代个体的方向可能存在更优的解，此时，可进一步寻优。

利用2个父代个体和子代个体构成初始复合形，并沿父代指向子代个体方向进行映射、扩张和收缩操作，当寻找到比子代个体更优秀且满足约束条件的新个体时，则用其取代子代个体，并继续寻优，直至找不到更好的满足约束条件的新个体。

2.5 免疫高频变异策略

传统的距离算法抛弃了遗传算法固有的变异过程[9]。然而，在多目标优化问题中，非支配解往往是连续的;即使对于不连续问题，多数非支配解也往往相邻。所以，基于当前非支配解信息，以寻求其附近非其他的支配解和比当前非支配解更好的解，是一种高效可行的寻优方案。

首先，对第 t代的非支配解 A(t)={a1(t)，a2(t)，…，aN(t)(t)}进行克隆操作，得到克隆群体A＇(t):

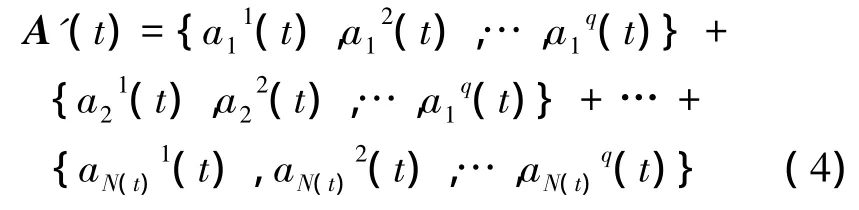
对得到的每个克隆个体，进行变异操作，将变异后满足约束条件的个体和已有的非支配解混合，并挑选出其中的非支配解;最后，对它们赋予相同的潜在值。

在传统的遗传算法中，变异算子与代数是没有直接关系的。从而当算法演化到一定代数以后，由于缺乏局部搜索，很难从后期变异中获得有效收益。为解决上述问题，Michalewicz[1]将变异算子的结构与演化代数联系起来，随着演化的推进，变异的范围越来越小，从而加强局部搜索。其具体操作如下:

设个体 s=(v1，v2，…，vk，…，vn)中的分量 vk被选中参与变异，其定义域是[ak，bk]，则变异后的个体为

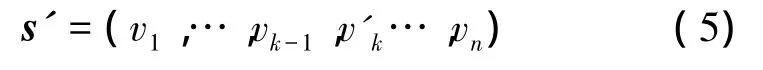
式中:

式中:rand是取0和1的随机数，t为当前演化代数，函数Δ(t，y)的具体表达式为

式中:r为[0，1]上的随机数;T为最大代数;λ是决定非一致性程度的参数，其取值一般为2～5。

图1给出了混合距离算法具体流程图。

2.6 算法测试

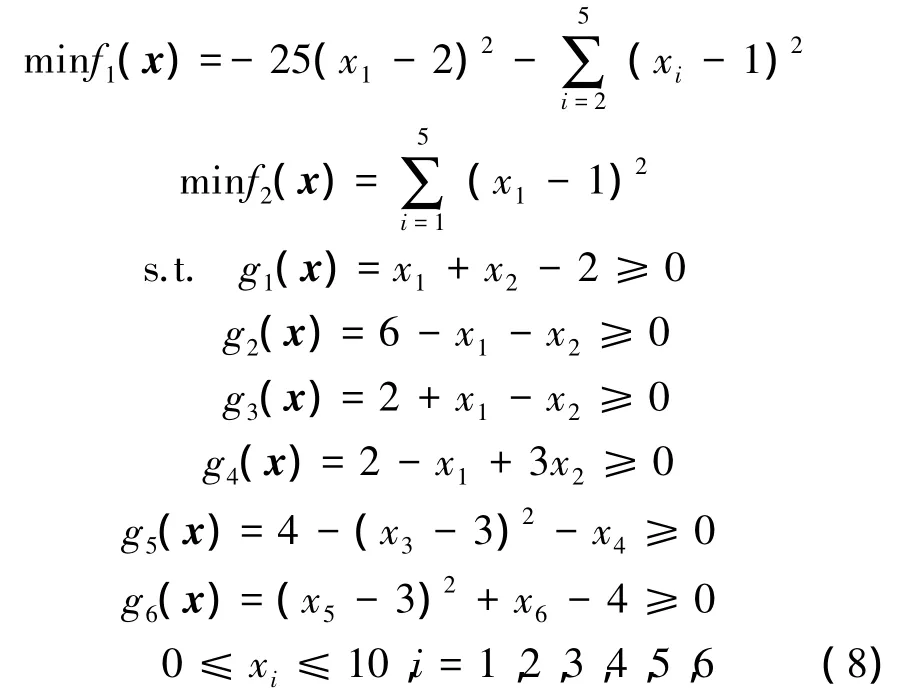
采用OSYCZKA和KUNDU提出的测试函数(式(8))[9]对比混合距离算法和原算法的性能。在2种算法中，取惩罚乘子r为1 000，初始潜在值为10。最大遗传代数为500，种群规模为800。图2对比了2种算法的非支配解群。

由图2可以看出，对于该测试函数，混合距离方法无论从非支配解的精度、数量、宽广性和均匀性上都明显优于传统距离方法。

图1 混合距离算法流程图Fig.1 The flow chart of the hybrid distance algorithm

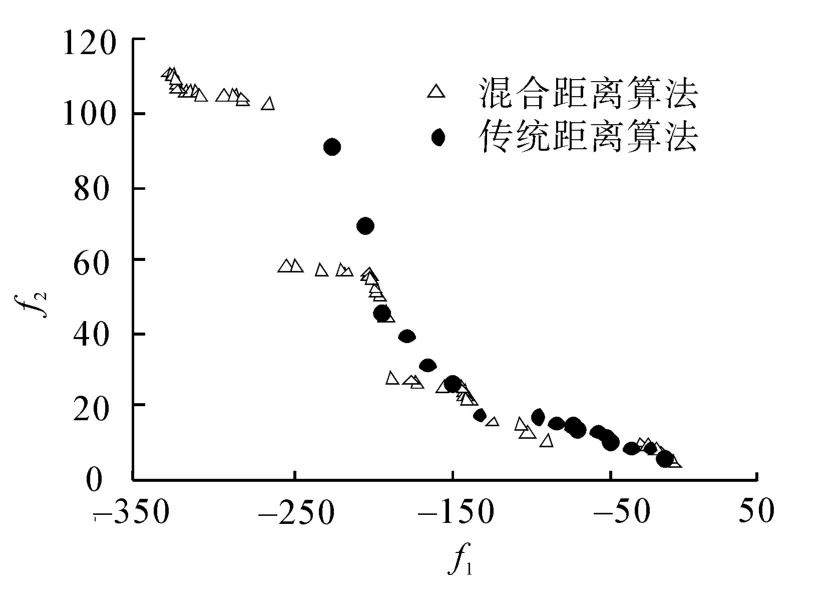
图2 混合距离算法与传统距离算法结果对比Fig.2 The results comparison between the hybrid distance algorithm and the traditional distance algorithm

利用TNK[1]标准测试函数比较混合距离算法和传统距离算法的性能。

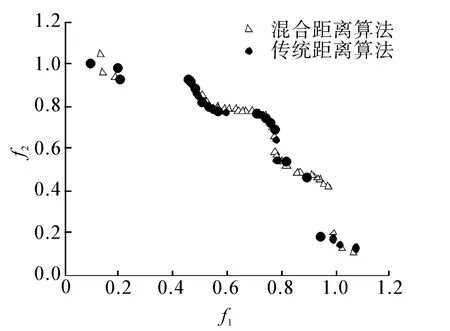
图3 TNK测试函数结果对比Fig.3 The comparison on TNK testing function results

对于TNK函数，混合距离算法与传统距离算法相比，在解的质量上，两者相当;但在解的均匀性和连续性上，前者较后者优。

文献[1]采用空间度量指标S，来衡量所得到非支配解的“均匀性”，其定义如式(10)。

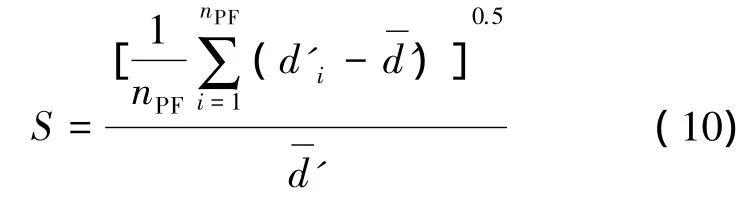
式中:m 为目标空间的维数，j=1，2，…，nPF。

如果S=0，则表示所得到的解点呈均匀分布。S越小，解的均匀性越高。

经计算，混合距离算法的S=0.75，传统距离算法的S=0.996 2。由此可知，混合距离算法所得到的非支配解的均匀性高。

由此可见，针对多目标问题，混合距离方法求解精度高，非支配解分布均匀且范围广泛。

3 蒸汽发生器多目标优化设计

在船舶核动力系统中，降低核动力设备重量有助于提高船舶的机动性及改善船员的生活居住条件;同时，降低冷却剂流量有助于减小主泵扬程和尺寸。因此，采用上述开发的混合距离算法，以蒸汽发生器重量和一次侧流量为目标，进行其优化设计。其中蒸汽发生器模型详见文献[6]。

选定一回路运行压力P、堆芯冷却剂进口温度Tin、堆芯冷却剂出口温度Tout、传热管外径d、传热管内冷却剂流速v、传热管节径比s/d这6个参数为优化变量。在满足蒸汽发生器和堆芯的设计约束条件下，通过合理地调整这些参数，以达到减小其重量和一次侧冷却剂流量的目的。

考虑热力性能、生产和施工等实际因素，表1给出了蒸汽发生器优化设计中所必须满足的约束条件[6]。

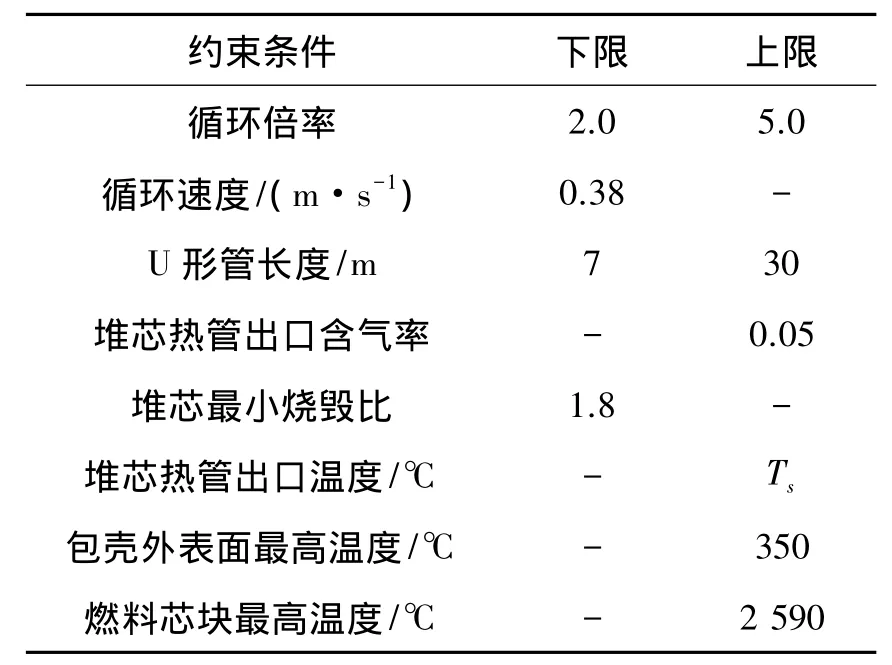
表1 蒸汽发生器优化的约束条件Table 1 The constraint conditions of the steam generator

图4给出了蒸汽发生器非支配解前沿面。从非支配解的分布可以看出:最优的蒸汽发生器重量和一次侧流量组合不是一条连续的曲线。

图4 蒸汽发生器多目标优化结果Fig.4 The multi-objective optimization results of the steam generator

文献[10]对这种不连续现象给出了解释:在以重量和流量为目标的蒸汽发生器多目标优化设计中，影响非支配解分布的关键参数是堆芯冷却剂进口温度(Tin)和传热管内冷却剂流速(v)。在图4中，沿第1段非支配解重量增加的方向，Tin逐渐减小，冷却剂平均温度逐渐降低，这使得传热面积逐渐增大;同时，在这个过程中，一次侧流量不断降低，使得传热管根数减少。因此，需要不断增加传热管的长度来保障所需的传热面积。随着Tin的继续降低，其最终会使得传热管长度达到约束上限，这时，已不能通过Tin达到降低流量的目的。在第2段和第3段非支配解中，传热管内冷却剂流速的降低导致了蒸汽发生器重量的增加和一次侧流量的降低。由于引起重量降低的原因不同，使得非支配解分布不连续。

在本文研究中，堆芯功率始终是保持不变的，在维持蒸汽发生器进出口温差不变的情况下，通过改变其他一些结构或运行参数是能改变蒸汽重量的。同时，从图4也可以认识到:在以蒸汽发生器重量和一次侧流量为目标的优化设计中，有2部分区域(蒸汽发生器重量在 187.5～195.0 t和 197.5～206.0 t)是可以不予考虑的，在这2个区域内，可以在维持几乎相同的一次侧流量下，而寻找到更优的重量。

4 结论

针对传统距离方法寻找非支配解精度不高、连续性不强、范围不广的缺点，本文通过引入复合形算法的深度搜索策略和免疫算法的高频变异策略，开发了一种混合距离算法。通过标准测试函数，以及实际应用，表明这种混合距离算法具有优良的性能，并得出以下结论:

1)混合距离算法能很好地处理多变量、多约束多目标问题，复合形和免疫算法的引入提高了传统距离算法的寻优能力，使得传统的距离算法寻优范围更广、连续性更强。

2)在追求以重量和一次侧流量最小的蒸汽发生器设计中，非支配解的前沿面不连续分布。

3)混合优化算法是多目标优化算法的一个重要发展方向，将全局优化算法与局部优化算法结合，能准确并精确地寻找到多目标问题的非支配解。

[1]焦李成，尚荣华，马文萍，等.多目标优化免疫算法、理论和应用[M].北京:科学出版社，2010:1，60，71，141.

[2]OSYCZKA A，KUNDU S.A new method to solve generalized multicriterion optimization problems using generic algorithm[J].Structural Optimization，1995，2(10):94-99.

[3]OSYCZKA A，KUNDU S.A modified distance method for multicriterion optimization using genetic algorithm[J].Computers and Industrial Engineering，1996，4(30):871-882.

[4]徐锦康.机械优化设计[M].北京:机械工业出版社，1996:77-82.

[5]刘成洋，阎昌琪，王建军.新型混合粒子群算法在核动力设备优化设计中的应用[J].哈尔滨工程大学学报，2012，33(4):534-538.LIU Chengyang，YAN Changqi，WANG Jianjun.Application of a new hybrid particle swarm optimization in the optimal design of nuclear power components[J].Journal of Harbin Engineering University，2012，33(4):534-538.

[6]秦慧敏，阎昌琪，王建军，等.立式自然循环蒸汽发生器的重量优化设计[J].原子能科学技术，2011，45(1):66-72.QIN Huimin，YAN Changqi，WANG Jianjun，et al.Optimal design of vertical circulation steam generator weight[J].Atomic Energy Science and Technology，2011，45(1):66-72.

[7]CHEN Lingen，ZHOU Shengbing，SUN Fengrui，et al.Preliminary design optimization of a steam generator[J].Energy Conversion and Management，2002，43:1654-1661.

[8]LIU Chengyang，YAN Changqi，WANG Jianjun.Optimal design of vertical natural circulation steam generator[J].Nuclear Engineering and Design，2012，252:167-178.

[9]玄光男，程润伟.遗传算法与工程优化[M].于歆杰，周根贵，译.北京:清华大学出版社，2005:76-77，103.

[10]CHEN Lei，YAN Changqi，WANG Jianjun.Multi-objective optimal design of vertical natural circulation steam generator[J].Progress in Nuclear Energy，2013，68:79-88.