开放式课堂，给数学学习插上一双腾飞的翅膀

肖正波

【摘要】课程标准明确指出，初中数学教学活动要向学生提供充分的从事数学活动的机会，帮助他们在自主探索与合作交流的过程中深入理解基本的数学知识与技能、方法与过程、情感态度价值观。新课程背景下，开放式数学课堂在培养学生的创新精神与探究意识能力方面有着得天独厚的优势，是目前数学课程改革活动中的一个发展潮流。当然，囿于种种因素，目前的数学开放式课堂还存在着种种不足。但不可否认的是，它已然在深入推进课程改革，全面提高教学质量方面产生了积极的意义和影响，给初中生数学学习插上了一双腾飞的翅膀。本文中，笔者就结合自己的教学实践，从转变观念，认识开放式数学课堂的内涵；以生为本，构建开放式数学课堂的模式；高效复习，升华开放式数学课堂的效率等几个方面展开论述。

【关键词】初中数学 开放式课堂 教学策略

【中图分类号】G633.6 【文献标识码】A 【文章编号】2095-3089（2014）09-0141-01

随着课程改革的逐步深入，崭新的教学理念，开放的课堂模式带给了我们强烈的心灵震撼，拓宽了教师的教学视野，提升了数学课堂的教学效率。作为一种全新的课堂模式，开放式课堂一改传统的以教师为中心的做法，从学生本位出发，尊重学生的主体地位，以促进全体学生的全面发展为目标，受到了广大师生的一致肯定与推崇。下面，笔者就自己在初中数学教学实践中的一些做法与诸位共享一二，期待得到各位专家的批评指正。

一、转变观念，认识开放式数学课堂的内涵

现代心理认知理论指出：初中阶段，每一名学生都有着强烈的被需求与被尊重的心理。为此，我们在课堂教学活动中要着眼于每一名学生的个性特点与心理认知，充分挖掘每一名学生的学习潜力，促进全体学生的全面发展。这既是开放式数学课堂的内涵，也是其科学构建的终极目标。对于数学学科来说，我们不仅要针对教材内容实施开放式策略，更要开放学生的数学活动，引导学生多思考、多发现、多探索，运用数学的视角去审视生活中的一些难题，促进其知识学习与创新能力的同步发展。

譬如，讲授函数知识的时候，笔者出示了这样一道题：

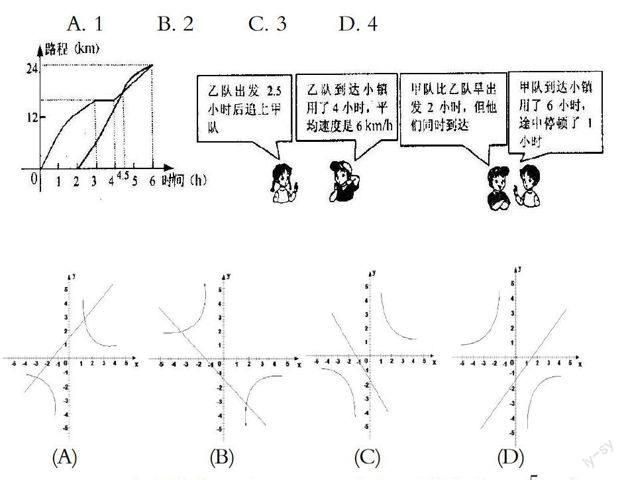
三军受命，我解放军各部队奋力抗战救灾一线。现有甲、乙两支解放军小分队将救灾物资送往某重灾小镇，甲队先出发，从部队基地到小镇只有唯一通道，且路程为24km，如图是他们行走的路线关于时间的函数图像，四位同学观察此函数图像得出有关信息，其中正确的个数是（ ）

A. 1 B. 2 C. 3 D. 4

这道题，将函数知识与学生日常生活中的行程问题紧密联系了起来，以课本知识为依托，创设了形象生动的社会问题情境，不但有效激发了学生的学习兴趣，更将学生的数学学习与实际能力紧密联系在了一起，培养了他们的探究意识与创新精神。

二、以生为本，构建开放式数学课堂的模式

有一名著名的教育家曾说：只有关注学生的潜在性，才会促使学生实现智慧和才能的发展。也就是说，在初中数学课堂上，我们需要以生为本，创设构建开放是课堂教学模式，变传统的学生被动接受为主动探究，大胆改革，积极创新，为学生迸发出无限的创新潜能与个性解放提供肥沃的土壤，展示的平台。

譬如，笔者在讲授八年级下册“数据的波动程度”时，就把课堂的主动权交给了学生，让他们自主阅读教材，根据教材知识及学生已有的生活经验与阅读积累，查阅、收集相关的问题情境与数据材料，小组合作，利用极差、方差、标准差等数学概念来判断某组数据的稳定性。不成想，没有了教师在课堂上条条框框的束缚，环环相扣的桎梏，他们所联想到的问题情境涉及各行各业，显示了当代中学生宽阔的视野与广博的知识积累。爱好体育的学生想到了不同乒乓球的直径与标准要求之间的误差，出身农村的学生想到了农作物株苗高低不等的长势，还有的学生想到了自己平时的考试成绩与班成绩之间的比较，有的学生想到了奥运会上射击项目每次激发时的环数……他们在完成数据分析的生活，不仅仅考虑到了数据的平均水平，更考虑到了数据的离散程度，进而顺利得出了极差的概念，突破了课堂教学的重点、难点，令教师感到非常满意。甚至于，一名平时在课堂上极少发言的中等生在小组活动中表现得非常积极，还引导小组很快得出了“一般而言，一组数据的极差、方差或标准差越小，这组数据就越稳定”的结论，令教师啧啧称奇，大为惊叹。

三、高效复习，升华开放式数学课堂的效率

复习课，是初中数学教学过程中非常重要的一种课型。它在巩固、梳理学生已有的课堂知识，促进数学知识系统化，提升学生数学应用能力等方面有着画龙点睛般的重要作用。遗憾的是，多年以来，数学复习课堂模式单调低效，无非就是做题，做题，再做题，只是“温故”，却没有能够有效地升华学生的数学能力与知识体系，严重影响着数学课堂的复习效果与效率，销蚀了学生的学习兴趣。于是，笔者在复习课上大胆尝试了开放式教学模式，让学生自己归纳单元知识，总结解题方法，讲解重点难点，达到了较好的课堂效果。

以“二次函数”这一单元的复习课为例，在开放的复习环境中，学生们不但自主归纳出二次函数的图像、增减性，最大值、最小值，与一元二次方程和不等式之间的关系，更是列举出了如下几个常见题型，极具代表性：

1.已知以x为自变量的二次函数y=（m-2）x2+m2-m-2的图像经过原点，则m的值是______。

2.下列各图中能表示函数和在同一坐标系中的图像大致是（ ）

（A） （B） （C） （D）

3.已知一条抛物线经过（0，3），（4，6）两点，对称轴为x=■，求这条抛物线的解析式。

總之，随着素质教育的深入进行，开放式课堂必将在今后的初中数学教学过程中扮演愈来愈为重要的角色。这便要求我们教师要积极转变教学观念，提升自己灵活处理课堂问题的应变能力，始终将学生的需求放在第一位，提升学生的解题能力、创新精神，为培养德才兼备、全面发展的世纪建设人才而不遗余力。

参考文献：

[1]王芳.谈初中数学开放式教学[J].学生之友，2013（11）.

[2]陈雨.初中数学开放性问题教学设计例析[J].数学学习与研究，2012（14）.