模糊集收敛的等价性
边梦柯,樊太和
(浙江理工大学理学院,杭州310018)
模糊集收敛的等价性
边梦柯,樊太和
(浙江理工大学理学院,杭州310018)
基于前人在对特殊模糊集上关于确界收敛,L-收敛,Endograph-收敛,Sendograph-收敛之间的等价性的分析,证明了一般模糊数序列上确界度量收敛等价于同时层次收敛和强截集收敛,并对关于截集连续的模糊数集合上的收敛的等价性给出了一种简洁的几何证明方法。
模糊数;上确界度量;截集收敛;强截集收敛
1 引 言
自模糊数的概念于20世纪70年代引入以来,已被人们从不同角度进行了深入研究。Kaleva,Greco等许多学者在模糊集的收敛方面做了大量的研究[1-2],Medar M R和Flores H R[3]在文献中讨论并证明了一种特殊的模糊集的上确界收敛、L-收敛、Endograph-收敛、Sendograph-收敛之间的等价性,但是证明过程繁琐。本文将讨论并证明对一般模糊数来说,上确界收敛等价于同时L-收敛和强截集收敛,本文还将对文献[3]中模糊集收敛的等价性给出一种简洁的几何证明方法。
1 模糊集收敛
设(X,d)是一个度量空间,A1,A2是X的两个非空紧子集,则A1,A2之间的Hausdorff度量H定义如下:

其中B(A,ε)={x∈X|d(x,A)<ε},d(x,A)=(x,a)。
用PK(X)表示所有X的非空紧子集构成的集合。众所周知,H是PK(X)上的一个度量,如果X是可分(完备)的,则PK(X)也是可分(完备)的。
上述度量H可等价定义为:

其中H*(A,B)=sup{d(a,B)|a∈A}。
设C,Cp(p=1,2,…)⊆X,称{Cp}Kuratowski收敛于C,如果
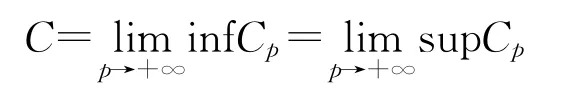
其中

<pi+1,i=1,2,…}=。
以下是Kuratowski收敛与Hausdorff收敛之间的关系及Hausdorff收敛的性质。
设{Cp}是一紧集序列,则{Cp}在Kuratowski意义下收敛于紧集C等价于{Cp}在Hausdorff度量下收敛于C。由于Kuratowski极限一定是闭集,因此有以下关系:
设{Cp}(p=1,2,…)是PK(X)中的一非降(增)序列,若存在{Cp}的一个子列在Hausdorff度量下收敛于C(∈PK(X)),则{Cp}在Hausdorff度量下收敛于C,即H(Cp,C)→0(p→+∞)。
设En={u:Rn→I|对所有α∈I,Lαu是非空紧集},其中

为u的α-截集,而

任取α∈[0,1),令Lα+u=(Lα+u称为u的α强截集)。则强截集有如下性质:若{αn}是I中任一单调递减收敛于α的子列,有→Lα+u(n→ +∞)。再令J(u)={α∈(0,1)|H(Lαu,Lα+u)>0}={u∈En|对任意的α∈[0,1],Lαu是关于α连续的}(当α=0或1时,Lαu的连续性分别为右或左连续)。则有:u∈当且仅当J(u)=Ø。
En上的上确界度量d∞定义为d∞(u,v)= supα∈(0,1]H(Lαu,Lαv)。(En,d∞)是完备但不可分的度量空间。
下面是模糊集的几种收敛定义。
定义0.1 (1)(d∞-收敛[3])设up,u∈En,p= 1,2,…。称up关于度量d∞收敛于u,如果d∞(up,u)→0(p→∞),简记为up→u(d∞)。
(2)(L-收敛[3])设up,u∈En,p=1,2,…。称up截集收敛于u,如果对任意的α∈(0,1],H(Lαup,Lαu)→0(p→∞),简记为up→u(L)。
(3)(L+-收敛)设up,u∈En,p=1,2,…。称up强截集收敛于u,如果对任意的α∈[0,1),H(Lα+ up,Lα+u)→0(p→∞),简记为up→u(L+)。
定理0.2[3]设up∈En,u∈,p=1,2,…,则下面结论是等价的:
(i)up→u(d∞);
(ii)up→u(L)且L0up→L0u(H)。
注:文献[3]中给出的定理0.2的(ii)⇒(i)的证明是一种分析方法,这一证明既要用到文献[4]的结论,又要用到该文中的预备工作(引理3.13,3.15),整个证明篇幅超过3页,因此证明过程非常复杂。本文将在下一节给出(ii)⇒(i)的一种几何证明方法,和文献[3]中的证明过程相比,本文给出的方法要直观简洁得多。
2 模糊集收敛的等价性证明
定理1.1 设u,v∈En,则存在α∈I,使得
d∞(u,v)=max{H(Lαu,Lαv),H(Lα+u,Lα+v)},即上确界度量关于截集或强截集是可达到的。
证明 因为d∞(u,v)=supα∈(0,1]H(Lαu,Lαv),所以对任意的n∈N,存在αn∈I,使得

不妨设{αn}是I中的一单调收敛子列,若{αn}单调递增收敛于α0,则对式(1)关于n取极限可得:

若{αn}单调递减收敛于α1,同样地,对式(1)关于n取极限可得:

因此由上面两式可得:d∞(u,v)=v)或d∞(u,v)=所以存在α∈I,使得d∞(u,v)=max{H(Lαu,Lαv),H(Lα+u,Lα+v)}。
命题1.2 设up,u∈En,p=1,2,…。则up→u(d∞)⇔up→u(L)且up→u(L+)。
证明 必要性:由d∞-收敛和L-收敛的定义可知:up→u(d∞)⇒up→u(L),因此只需证明up→u(L+)即可。
对任意的α∈[0,1),取I中的收敛于α的一个单调递降列{αn},由上确界度量d∞的定义可知:对上述所有的αn,有d∞(up,u)≥H。再令n→∞可得:d∞(up,u)≥H(Lα+up,Lα+u)。又因为up→u(d∞),即d∞(up,u)→0(p→∞),所以H(Lα+up,Lα+u)→0。再由α的任意性可得:up→u(L+)。
充分性:假设up→/u(d∞),则存在ε0>0,对任意的p0∈N,存在p≥p0,使得d∞(up,u)≥2ε0,即存在αp∈I,使

于是满足式(2)的αp有无限个,且不是无限重复的,否则与假设矛盾。因此{αp}有收敛子列设收敛于α0,进一步可假设单调收敛于α0。为书写方便,用{αp}代替其子列,即{αp}单调收敛于α0。
若{αp}单调递增收敛于α0,则由式(2)和截集函数的左连续性可得:≥ε0,与up→u(L)矛盾,因此{αp}单调递减收敛于α0。
下面所举的两个例子说明命题1.2中的up→u(L)和up→u(L+)两个条件是必不可少的,且两者之间没有必然联系。
例1 设up,u∈E1,p=3,4,…,且

显然up→u(L),+up=[1,2],+u={2},但,d∞(up,u)=1。
例2 设up,u∈E1,p=3,4,…,且

显然up→u(L+)={2},=[1,2],但=1,d∞(up,u)=1。
下面的定理是截集收敛的一个重要性质,由此定理得到的推论即是文献[3]中的引理3.15。
定理1.3 设up,u∈En,p=1,2,…,且up→u(L),L0up→L0u(H)。设α,αp∈[0,1](p=1,2,…)且α∉J(u),若αp→α,则=0。
证明 因为α∉J(u),所以对任意的ε>0,存在δ>0,使

因为αp→α,所以对上述的δ>0,存在p1∈N,当p≥p1时,有α-δ<αp<α+δ。又因为up→u(L),所以对上述的ε>0,存在p2∈N,当p≥p2时,有

令p0=max{p1,p2},则对上述的ε>0,当p≥p0时,有

且

因此对任意的ε>0,存在p0∈N,当p≥p0时,有

证毕。
推论1.4[3]定理1.3中的条件“α∉J(u)”换成“u∈”后,结论恒成立。
下面笔者给出定理0.2中(ii)⇒(i)的一种几何证明。
设up,u满足定理0.2中的假设及条件(ii)。对任意p∈N,令fp(α)=H(Lαup,Lαu),则对任意的α∈(0,1],fp(α)→0(p→∞)。

又因为up→u(L),所以对上述的ε>0,存在p0∈N,使当p≥p0时,有

令B(α0,δα0)是α0的δα0开邻域(当α0为0或1时,同理分别可得0与1的半闭半开和半开半闭邻域),则{B(α0,δα0):α0∈I}构成I的一个开覆盖。由I的紧致性可知:有有限个B(α0,δα0)构成I的一个有限覆盖。因此要证明fp(α)在I上一致收敛于0,只需证明对任意的α∈(0,1),fp(α)在某一个开邻域B(α0,δα0)上一致收敛于0且fp(0)、fp(1)分别在[0,δ0),(δ1,1]上一致收敛于0即可。这里仅证明α0∈(0,1)的情形,α0=0,1的情形可类似证明。
对任意的α∈B(α0,δα0),对上述的ε>0,当p≥p0时,有

所以fp(α)在B(α0,δα0)上一致收敛于0,这就证明了fp(α)在I上一致收敛于0。
因此对任意的ε>0,存在p0∈N,使当p≥p0时,|fp(α)|<ε。从而

即d∞(up,u)→0(p→∞),证毕。
[1]Kaleva O.On the convergence of fuzzy sets[J].FuzzySets and Systems,1985,17:53-65.
[2]Greco G H,Moschen M P,Rezenda E Q F.On the variational convergence of fuzzy sets in metric spaces[J]. Ann Univ Ferrara-Sez VII-Sc Mat,1998,44:27-39.
[3]Medar M R,Flores H R.On the equivalence of convergence of fuzzy sets[J].J Fuzzy Sets and Systems,1996, 80:217-224.
[4]Kuratowski K.Introducción a la Theoria de Conjuntos y a la Topologia[M].Barcelona:Vicens-Vives,1966.
[5]Diamond P,Kloeden P.Metric Spaces of Fuzzy Sets:Theory and Applications[M].Singapore:World Scientific,1994.
Equivalence Property of Convergence of Fuzzy Sets
BIAN Meng-ke,FAN Tai-he
(School of Sciences,Zhejiang Sci-Tech university,Hangzhou 310018,China)
Base on the previous analysis of equivalency among clear boundary convergence,L-convergence,Endograph-convergence and Sendograph-convergence in special fuzzy sets,This paper proves that supremum metric convergence is equivalent to simultaneous level convergence and strong cut set convergence for general fuzzy number sequences and meanwhile gives a geometric method to prove the equivalence property of convergence on continuous fuzzy number set about cut set.
fuzzy number;supremum metric;cut set convergence;strong cut set convergence
O189.13
A
(责任编辑:马春晓)
1673-3851(2014)01-0079-04
2012-06-01
国家自然科学基金项目(11171308)
边梦柯(1987-),女,河南许昌人,硕士研究生,主要从事不确定性的数学理论研究。

