筒子染色机染缸碟形封头的可靠性优化设计

许锐敏，潘 骏，陈文华，王 孟，许成彬

（浙江理工大学浙江省机电产品可靠性技术研究重点实验室，杭州310018）

筒子染色机染缸碟形封头的可靠性优化设计

许锐敏，潘 骏，陈文华，王 孟，许成彬

（浙江理工大学浙江省机电产品可靠性技术研究重点实验室，杭州310018）

染缸的碟形封头对筒子染色机使用的安全可靠性有着极其重要的影响。以筒子染色机染缸碟形封头为研究对象，采用ANSYS Workbench软件对其进行参数化建模和有限元分析；通过灵敏度分析得到了影响其等效应力和总变形的关键参数，利用实验数据法和多目标驱动优化方法对封头的结构尺寸进行优化设计；建立考虑应力和变形相关性的可靠性计算模型，运用6西格玛设计准则和拉丁超立方体抽样方法，得到了最大等效应力和最大总变形的概率分布，得出了优化前后封头的可靠度，并且优化后可靠度有明显提高。

染缸；碟形封头；ANSYS Workbench；灵敏度分析；可靠性优化设计

0 引 言

筒子染色机是纱线染色机中的一种，通过循环泵控制染液在染缸内循环流动，对纱锭进行染色。筒子染色机的主要结构包括染缸、循环泵、热交换装置和控制系统等，而其中染缸是由缸盖和缸身组成的封闭压力容器，由于恶劣的工作环境，其使用的安全可靠性引起了广泛的关注。碟形封头又称带折边的球形封头，是压力容器凸形封头的一种，由于制造简单而被广泛应用于中、低压压力容器。随着染整行业的不断发展，碟形封头的需求量越来越大，对碟形封头使用的安全可靠性要求也日益提高，人们也逐步开始重视碟形封头在参数不确定情况下的可靠性研究。

传统的压力容器封头设计大多采用常规的安全系数设计法［1］，由于常规设计未考虑影响因素的不确定性情况，因此许多学者对压力容器封头可靠性设计进行了研究。胡宜生［2］假设各设计参数都服从正态分布，利用静力学建立应力的计算公式，并得到其概率分布，从而利用应力-强度干涉理论计算其可靠度。农琪［3］以应力-强度干涉理论为基础对压力容器椭圆形封头进行了可靠性设计。周鹏飞［4］利用ANSYS软件的可靠性分析功能和优化设计功能对异形封头的可靠性分析和优化进行了研究。彭翠玲［5］运用ANSYS的概率设计功能，以压力容器的壁厚、压力载荷及弹性模量为随机输入变量，利用蒙特卡罗抽样方法，获得了压力容器封头有限元分析模型的应力概率分布特征。上述方法仅考虑了应力和强度的随机性，未考虑变形的影响及其与应力之间的相关性。

本文以筒子染色机的碟形封头为研究对象，利用有限元分析软件ANSYS Workbench对碟形封头进行参数化建模和有限元分析，利用多目标驱动优化方法对封头的结构尺寸进行优化设计；运用6西格玛设计准则，来得到最大等效应力和总变形的概率分布；建立考虑应力和变形相关性的可靠性计算模型，验证优化方案的可行性。

1 筒子染色机染缸碟形封头结构简介

碟形封头主要由球冠、过渡圆弧环和短圆筒三部分组成。GF241XL-21型筒子染色机染缸的筒体内径Di=210 mm，据GB 150-2011《压力容器》和JB/T 4746-2002《钢制容器用封头》；其碟形封头的球冠半径Ri=0.9 Di=189 mm，过渡半径r= 0.17 Di=35.7 mm，圆整后取r=36 mm；碟形封头计算厚度δ1=0.64 mm，考虑到钢板负偏差及腐蚀裕量，参考钢材标准规格取碟形封头名义厚度［6］δ1n=3 mm；染缸外径和内径的比值K=Di+2δ/Di= 210+6/210=1.028＜1.2，属于薄壁容器［7］，薄壁筒体的计算厚度δ2=0.54 mm；同理取筒体的名义厚度δ2n=3 mm。当筒体长度大于时，可以不考虑筒体过渡区存在的边缘应力的影响，取筒体长度为90 mm。根据ASMEⅧ-1［8］可知过渡区均需要1∶3的斜面过渡，筒子染色机的碟形封头的结构如图1所示。

图1 碟形封头结构

2 碟形封头的有限元分析

2.1 碟形封头参数化建模

碟形封头属于轴对称结构，采用2D建模和面体分析，可以节约计算时间。在对模型进行网格划分时，采用自动划分网格的方式，取单元尺寸为0.5 mm时可以得到划分细密的网格，此时的单元个数为3 570个。碟形封头的材料设置为奥氏体不锈钢，密度ρ=7.93×103kg/m3，弹性模量E=200 GPa，泊松比μ=0.3。

施加合理边界条件是保证仿真结果正确性的关键。在进行仿真分析时，需结合碟形封头的实际受力情况设置边界条件。如图2所示，（a）在筒体上端面约束Y方向的位移，（b）在球冠区对称面上约束X方向的位移，（c）在封头内壁上施加均布内压载荷，p=0.5 MPa。从图3仿真分析结果可知施加的载荷和约束与碟形封头的实际工作情况是相符的。

图2 碟形封头边界条件

2.2 有限元仿真分析

通过有限元仿真分析得到的碟形封头应力应变云图如图3所示。图3（a）显示等效应力最大值出现在球冠区与过渡区连接处，最大值为33.08 MPa；图3（b）显示总变形最大值出现在球冠区，最大值为0.04 mm。材料的许用值为［σ］tφ=115.2×0.85= 97.92 MPa，一般总变形不得超过3%，即许可变形量为［ξ］=0.09 mm，应力和总变形符合压力容器设计规范要求。

图3 仿真分析结果

3 碟形封头的可靠性优化设计

3.1 碟形封头相关参数的灵敏度分析

由于材料属性、几何尺寸、载荷等不确定性参数，对碟形封头的应力和变形有不同程度的影响，因此通过灵敏度分析来找出敏感性较大的参数。参考机械设计手册，并假设该碟形封头的相关设计参数均服从正态分布，可确定设计参数的平均值和标准差如表1所示。

表1 输入参数取值

灵敏度的目标函数是设计变量的导数，即随机变量分布函数的变化引起失效概率变化的比率，可以用来评定输入参数对输出变量的影响程度。通过ANSYS Workbench仿真分析所得的灵敏度柱状图［10］如图4所示。从图4可以直观地看出输入参数对输出参数的敏感程度：其中输入参数球冠区过渡半径（P7）、球冠半径（P8）和封头厚度（P11），内压载荷（P13）对输出参数最大等效应力和最大总变形的影响较大。

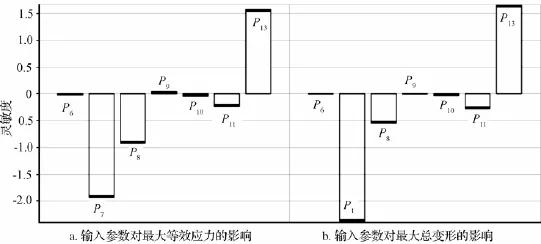
图4 碟形封头灵敏度分析结果

3.2 碟形封头多目标驱动优化设计结果

在ANSYSWorkbench中，根据上述结构参数和灵敏度分析结果，可将灵敏度较高的关键结构参数优化的重要性设置为高，灵敏度较低的结构参数设置为低。运用实验数据法（DOE）进行响应面拟合，即在设置好的各结构参数的取值范围内，利用数理统计方法和正交原理，从大量的设计点中挑选出具有代表性和典型性的设计点，并通过响应面法拟合计算出45个更新的设计点。在多目标驱动优化（GDO）时，取初始样本数为1 000，以等效应力最大值最小化和总变形最大值最小化为优化目标，程序基于此目标从上述更新的45个设计点中自动选取最合适的3个候选点，如表2所示。

表2 碟形封头相关参数优化候选点

对比表2中的三个候选点，综合考虑等效应力最大值和总变形最大值以及结构尺寸参数取值，选择B点作为新的设计点。与未优化前的等效应力最大值和总变形最大值对比，等效应力最大值减小了32.3%，总变形最大值减小了45.0%。

3.3 碟形封头可靠性计算模型

碟形封头的可靠度可以定义为应力S小于强度δ且同时总变形D小于允许变形量ξ的概率。假设应力、强度、总变形量和允许变形量均服从正态分布，即

S～N（μS，），δ～N（μδ），D～N（μD），ξ～N（μξ），

令x=S-δ，y=D-ξ，则x和y分别服从均值为μx=μS-μδ和μy=μD-μξ，标准差为σx=和的正态分布，则随机变量x和y的概率密度函数可表示为：

当x＜0且y＜0时，碟形封头正常工作，其可靠度R可表示为：

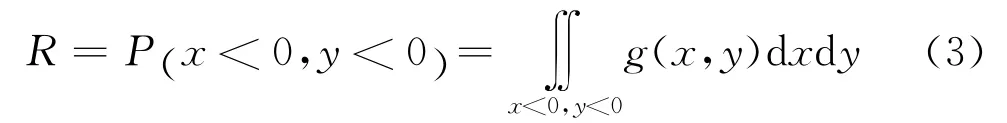
其中，g（x，y）表示变量x和y的联合分布密度函数，由于变量x和y均服从正态分布，则其联合密度函数为：

其中，ρ称为相关系数，其定义为：

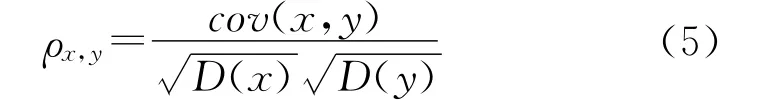
若变量x和y不相关，则ρ=0；若变量x和y呈线形关系，则｜ρ｜=1。

利用ANSYSWorkbench中的6西格玛设计准则，假设输入的各结构参数均为服从正态分布的的变量，并且优化前后的结构参数的方差均取表1中的方差值；根据碟形封头实际承载情况，假设施加的内载荷也是一个均值为0.5 MPa，方差为0.1 MPa的正态分布。运用拉丁超立方体抽样［11］方法随机抽取800个样本，得到优化前后碟形封头最大等效应力和最大总变形的概率密度，结果如图5所示。

图5 碟形封头6西格玛分析结果

从图5可见，最大等效应力和最大总变形近似服从正态分布。优化前最大等效应力的均值估计值=39.3 MPa，标准差估计值=17.8 MPa，优化前最大总变形量估计值=0.046 mm，标准差估计值=0.024 mm；优化后最大等效应力的均值估计值=27.4 MPa，标准差估计值=12.2 MPa，优化后总变形量估计值=0.026 mm，标准差估计值=0.013 mm。取强度和许可总应变的变异系数为0.2，即可认为强度δ是服从均值为μδ =97.9 MPa，标准差为σδ=19.6 MPa的正态分布，许可变形量ξ是服从均值为μξ=0.09 mm，标准差为σξ=0.018 mm的正态分布。相关系数ρ可由模拟数据利用式（5）估计得出，其估计值ˆρ=0.97。

那么优化前随机变量（x0，y0）～N（-58.3，-0.044，26.472，0.0302，0.97），优化后随机变量（x，y）～N（-70.5，-0.064，23.092，0.0222，0.97），通过式（3）可靠度计算公式可以得出优化前碟形封头的可靠度R0=0.922 8，优化后可靠度R= 0.998 0。可见，优化后可靠度有明显的提高。

4 结 论

以筒子染色机染缸的碟形封头为研究对象，利用ANSYS Workbench软件建立了其参数化模型，并进行了有限元分析；通过灵敏度分析，得到了影响碟形封头最大等效应力和最大总变形的关键参数；利用实验数据法（DOE）和多目标驱动优化方法（GDO）从45个设计点中确定了最佳设计点；建立了考虑应力和变形相关性的可靠性计算模型，运用6西格玛设计准则和拉丁超立方体抽样方法，得到了优化前后最大等效应力和总变形的概率分布，得出了优化前后封头的可靠度，表明优化后可靠度有明显提高，验证了本文提出方法的可行性。

［1］胡宜生.压力容器封头的可靠性设计［J］.安庆师范学院学报，2006（12）：25-26.

［2］王心明.工程压力容器设计与计算［M］.北京：国防工业出版社，2011：24-25.

［3］农 琪.压力容器椭圆形封头的可靠性设计［J］.装备制造技术，2010（9）：53-54.

［4］周鹏飞，董金善，杨益清，等.基于ANSYS的异性封头可靠性分析与优化设计［J］.机械设计与制造，2012（1）：28-30.

［5］彭翠玲，艾华宇，刘青松，等.基于ANSYS的压力容器可靠性分析［J］.核动力工程，2009，30（1）：109-111.

［6］金秋红.关于压力容器设计时厚度的讨论［J］.价值工程，2010（7）：116-117.

［7］李福宝，李 勤.压力容器及过程设备设计［M］.北京：化学工业出版社，2009：36-38.

［8］Code P V.Rules for construction of pressure vessels［S］.

［9］Anghel C，Laz A I.Risk assessment for vessels affected by corrosion［J］.Chemical Engineering，2005，49（2）：103-118.

［10］王金龙.高压力容器筒体与封头连接区可靠性分析［J］.设计与研究，2007（8）：4-6.

［11］刘纪涛.基于拉丁超立方抽样及响应面的结构模糊分析［J］.机械强度，2011，33（1）：73-76.

Reliability Optimization Design for Dished Head of Dye Vat of Cone Dyeing Machine

XU Rui-min，PAN Jun，CHEN Wen-hua，WANG Meng，XUCheng-bin
（Zhejiang Key Laboratory of Reliability Technology Research for Mechanical and Electrical Products，Zhejiang Sci-Tech University，310018，China）

Dished head of dye vat has extremely important influence on the safe reliability of the use of cone dyeing machine.With dished head of dye vat of cone dyeing machine as the research object，this paper conducts parametric modeling and finite element analysis on it with ANSYS Workbench；obtains key parameters influencing its equivalent stress and total deformation through sensitivity analysis and conducts optimization design for the structure size of the head with experimental data method and multi-objective driven optimization method；establishes a reliability calculation model considering stress and deformation correlation and obtains the probability distribution of maximum equivalent stress and maximum total deformation and the reliability of head before and after optimization with Six Sigma design criteria and Latin Hypercube Sampling method.The result shows that the reliability is greatly improved after optimization.

dye vat；dished head；ANSYS Workbench；sensitivity analysis；reliability optimization design

TH136

A

（责任编辑：张祖尧）

1673-3851（2014）01-0006-05

2013-04-26

国家自然科学基金（51075370，51275480），浙江省重点科技创新团队（2010R50005），浙江理工大学科研启动基金（1103824-Y）资助项目。

许锐敏（1989-），女，湖北咸宁人，硕士研究生，主要从事机电产品可靠性研究。