基于遗传BP神经网络组合模型的中药销售预测研究

马 健，盛 魁

（亳州职业技术学院信息工程系，安徽 亳州236800）

中药是中国的国粹之一，数千年来用于预防保健、治病救人，为人类做出了巨大的贡献。随着国家对中医药产业重视程度的不断提高，人们对传统中医有了新的认识，到医院治疗服用中药的人数增多。这就要求医院保证库存中药能够为临床使用提供合理的供应量，同时要保证药品的质量。本文采用遗传算法对BP神经网络预测方法进行改进，从而有效解决基于BP学习方法的学习过程较长、收敛速度缓慢等问题。将改进后的BP神经网络组合模型应用于中药销售预测研究，并结合某医院的中药实际销售数据，进行实证研究。准确的中药销售预测对于医院减少库存、科学管理中药及提供科学决策等具有重要意义。

1 BP神经网络设计的构建

1.1 BP神经网络定义

BP结构神经网络是目前在数值预测中应用较为广泛的算法之一，Rumelhart带领的研究小组在1985年最先给出了BP算法的准确定义，目前有多种变化形式。非线性映射能力是其突出特点，通过有导师的训练模式来学习样本中包含的特有规律，然后将规律映射到神经网络各层的连接权值和阈值，经过信息正向传播和误差反向传播不断调整，从而使网络预测输出同期望输出逐步接近，最终使误差趋向于最小。

作为一种前馈型神经网络，其网络结构包括3部分：输入层、隐藏层和输出层，隐藏层的数量取决于问题的复杂程度，一般只有在当前的隐藏层神经元数量较多而不能进一步改善网络性能时考虑增加隐藏层。[1]本文主要通过长期大量样本的训练来预测中药应用的变化，为中药应用走势提供辅助参考，因此单隐藏层可以满足预测的精度需要。网络拓扑结构如图1所示。

图1 BP神经网络结构示意图

在图1中，a1，a2…，an为BP神经网络的输入样本，b1，b2，…bm为BP神经网络的输出结果，输入层与隐藏层之间的权值为εij，隐藏层与输出层的权值为εik，作为典型的非线性函数，BP神经网络反映的是一种函数映射关系。[2]

1.2 BP神经网络训练步骤

BP神经网络的训练一般包括以下步骤：

（1）网络初始值的设定。网络初始值包括学习速率、网络训练次数、误差精度的设定、各层之间的连接权值和阈值的初始化。

（2）隐藏层输出设定。根据输入样本，结合输入层和隐藏层间连接权值以及隐藏层阈值，得到隐藏层输出公式：

（3）输出层输出设定。由上一步隐藏层输出结果，结合本层的连接权值和阈值，计算输出层的输出结果公式为：

（4）预测误差计算。根据网络模型的输出结果来对比期望输出值之间的误差：

（5）根据网络预测误差进一步调节阈值和网络连接权值。

（6）判断算法迭代是否结束，若没有结束，返回步骤。

1.3 BP神经网络存在不足

BP神经网络作为一种演算过程清晰、具有复杂非线性映射功能的成熟算法，目前在人工神经网络中应用广泛。理论上，在拥有足够隐藏层和隐藏节点前提下可以逼近任意的非线性映射关系，同时具备良好的泛化能力和容错性。但BP神经网络作为典型的前馈型神经网络，缺点也同样明显：其梯度下降法的本质确定了学习过程较长，收敛速度缓慢；在收敛的同时可能会产生局部极小值或部分静态点，从而导致系统存在较大误差；初始权值和阈值设定随意性较大；对隐藏层和隐藏层节点的设定无成熟理论指导，需依靠经验和实验。

以上缺点的存在，加上病人人员变化情况，单纯使用BP神经网络预测中药销售的精度达不到预期，因此考虑加入遗传算法来对BP神经网络进行优化，使其能够更准确得出初始权值及阈值。

2 遗传BP组合网络模型构建

2.1 遗传算法

遗传算法是根据生物演变的进化规律得来的，美国的J.H.Holland教授通过实验发现，学习通过一个种群的进化适应实现比单个生物体的适应完成的要好，Holland在研究遗传算法中发现自适应是从所处的环境中得到反馈的函数关系，这种遗传算法是在一个固定种群中，个体使用固定的基因链，用适应度来随即选择双亲，并按交叉和变异算子来产生新的种群。该算法主要通过编码、选择、交叉和变异操作对群体中的对象一一筛选，保留适应度高的个体，使群体继承优点的同时优于前代，这样通过一代又一代优化使种群更适应环境，末代种群中的最优个体可以作为问题的近似最优解。[3]

遗传算法的基本运算流程如下：

（1）确立编码方式：遗传算法的编码机制仿照生物基因排序，需要将解空间映射到编码空间，对象按照设定规则排列成串，数据处理后需要进行种群的初始化。

（2）初始化参数：在遗传算法的实际操作时，需要在运行初始化时确定一些参数的值。这些参数包括串长、每一代群体的大小、交叉率、变异率、遗传代数等。

（3）设定适应度函数：该函数用于计算个体适应度值，是进行优胜劣汰的遗传操作的主要衡量指标。

（4）遗传操作：遵循自然界遗传规律，由选择、交叉和变异3种操作构成。选择操作是根据个体适应度的高低来筛选出符合条件的优秀个体，淘汰适应度值低的个体；交叉是将群体中的个体交换部分自带基因，从而产生一定概率的优秀基因组合；变异操作是模仿自然界生物体的基因突变，实现对算法搜索范围的扩展。3种操作共同作用于群体，从而产生出新一代的种群。

（5）结束条件：算法的结束取决于算法是否执行完规定的迭代次数或者经过多代进化的种群是否在性能上满足要求。

2.2 遗传算法优化BP神经网络

基于遗传算法来优化BP神经网络主要有3种方式：一种对BP网络结构的优化来消除多余节点和网络连接权；一种是利用遗传算法遗传操作优化出适应度最高的权值，来提高BP网络的学习效率，从而最大限度降低初始权值对网络结构的不利影响；还有一种是将上述两种方式结合。本例中主要利用遗传算法来优化BP网络的初始权值及阈值。设计步骤主要包括以下部分：

（1）建立3层BP网络模型

由于3层BP模型可以涵盖映射大部分连续函数，为避免网络结构过于复杂和减少权值训练时间，本实验采用的是单隐藏层的3层网络结构。

（2）初始化种群

在缺少经验的前提下，以随机的方式在遗传算法的解空间中产生初始种群，虽然该方法会导致初始群体在解空间分散不均，但该方法适应面广。个体编码采取实数编码，由输入层、隐藏层及输出层的连接权值和阈值来组成每个个体的实数串。

（3）进行适应度函数的计算

遗传算法依据种群中个体的适应度，向种群中适应度最高的方向搜索，选择合适的适应度函数将有利于寻求最优解。一般适应度函数通过对目标函数进行线性尺度映射变换而成。

在上式中，n为初始种群的大小。为避免初始权值和阈值的随机性对适应度函数计算的影响，在对每一个个体计算适应度函数值时，均采用遗传算法对BP神经网络的权值和阈值进行优化。

（4）遗传操作

这一步需要将遗传代数、交叉概率、变异概率根据多次实验测试结果设定，利用Matlab软件中的GAOT工具箱完成遗传操作。

重复步骤（2）至步骤（4），直到优化结果达到预测要求，结束循环，将优化后的参数值带入BP神经网络继续仿真。遗传算法优化BP网络流程如图2所示。

图2 遗传算法优化BP网络流程示意图

3 中药销售的预测及分析

某医院在临床治疗过程中，患者对中医诊治和中药使用备受亲睐。由于使用中药治疗避免了西药对人体的副作用，更有利于人们的身体健康，近几年中药的使用已经达到药品使用量的15%。为了更准确地掌握医院中药的销售情况，对2010－2012年医院中药的销售数据进行科学分析，能够为今后医院中药的销售情况进行预测。

3.1 数据采集

对某医院数据库中的数据进行整理，收集了2010－2012年的中药处方，并对处方中的中药进行分类和归纳，数据见表1和表2。

表1 2010－2012各年中药总体使用情况

表2 2010－2012年销售排前10位中药销售量

3.2 数据分析

依据表1和表2中的数据，分别利用BP网络和GMBP网络2种算法进行参数设定。主要涉及到两个方面：一方面包括BP网络中隐藏层节点数和初始化参数的设定；另一方面包括遗传算法中遗传代数等参数的设定。

3.2.1 BP中隐藏层参数的确定

对于BP网络而言，由问题复杂程度来决定设定层数，本文选用包含输入层、隐藏层和输出层3层基本结构，通过增减神经元数量来实现改善网络性能。隐藏层神经元个数的设定对系统影响较大，如果节点数过少网络将不能建立复杂的映射关系，网络预测误差较大，但是节点数过多又会出现 “过拟合”现象。目前对于隐藏层节点数的设定没有较为科学的方法，因此本文使用常见的经验公式来给隐藏层神经元个数划定范围，再通过对同一样本的训练来比较评估，综合训练精度和收敛速度两个量化指标来确立最优隐藏节点个数。[4]在实验中，通过经验公式的计算将隐藏层节点个数范围作了适当放大，在4～12之间逐一尝试，通过结果对比，将参数设定在6或7时误差最小，同时收敛速度也比较快。

3.2.2 BP中初始参数设定

本文使用Matlab工具箱中的newff来构造BP神经网络，程序如下：

net＝newff（minmax（p），[x，y]，｛＇tansig＇，＇purelin＇｝，＇trainlm＇）；x为网络输入节点数，y为网络输出节点数，tansig为网络的训练函数另外根据对隐藏层节点数的测试结果分析，一般在2 000以内无法收敛，超过2 000以后收敛概率较小，且预测精度不高，因此将学习次数设定为2 000。另外根据多次实验测试的结果，将目标误差设定在0.001，学习速率设定为0.4。

主要程序如下：

net.trainParam.show＝100；

net.trainParam.epochs＝2000；

net.trainParam.goal＝1e－3；

net.trainParam.lr＝0.4

[net，tr]＝train（net，p，t）；

3.2.3 遗传算法参数设定

根据前面分析，对遗传算法的参数设定主要包括对迭代次数、种群规模、交叉概率和变异概率4个方面。参数设定如下：迭代次数100次、种群规模为50、交叉概率为0.3、变异概率为0.2，得出对各中药使用数量的BP预测值和GMBP预测值，如表3所示。

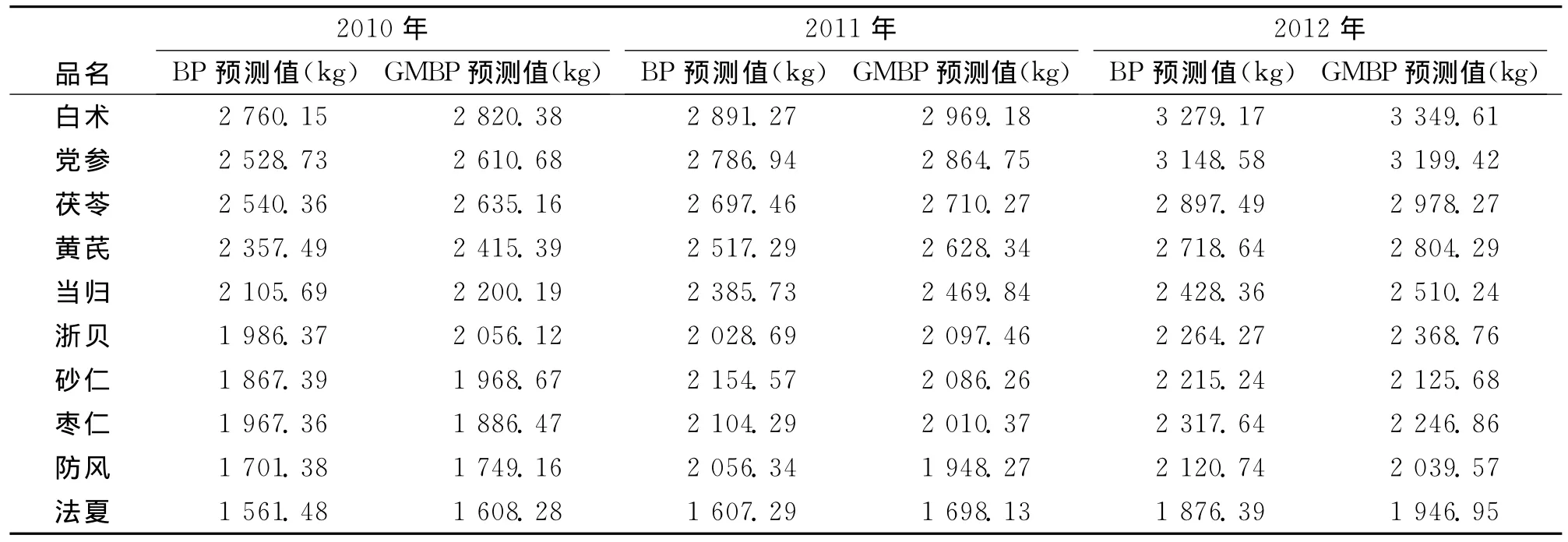
表3 2010－2012各年中药使用情况的两种预测比较

3.3 结果分析

根据表3的数据计算出两种预测的误差率，例如，2010年白术的BP预测的误差率是3.634%，而GMBP预测的误差率是1.532%；枣仁的BP预测的误差率是－6.100%，而GMBP预测的误差率是－1.738%；2011年党参的BP预测的误差率是3.755%，而GMBP预测的误差率是1.068%；防风的BP预测的误差率是－7.086%，而GMBP预测的误差率是－1.459%；2012年茯苓的BP预测的误差率是3.462%，而GMBP预测的误差率是0.770%；砂仁的BP预测的误差率是－5.495%，而GMBP预测的误差率是－1.195%。从2010－2012年随机取得预测的误差率可知，GMBP的预测值要比BP预测的值精准。

4 小 结

本文在传统BP神经网络算法的基础上，引入遗传算法改进BP神经网络预测模型，解决了网络收敛速度慢、易陷入局部极小的缺陷，能有效提高算法的精度，提高了网络学习能力。分别采用传统的BP神经网络和改进BP神经网络对中药销售进行仿真实验。实验结果表明，改进的BP神经网络对中药销售的预测精度较高，为医院今后的中药管理提供了科学依据。

[1]刘红，任坤，陈文凯.神经网络的BP训练算法和遗传优化训练算法的对比研究[J].北京工业职业技术学院学报，2008，7（02）：31－34.

[2]马新强.基于BP神经网络的用药品销售预测模型设计[J].重庆文理学院学报，2008，27（02）：64

[3]段玉倩，贺家李.遗传算法及其改进[J].电力系统及其自动化学报，1998，10（01）：39－52

[4]王晨光.基于主成分分析的BP神经网络在药品销售预测中的应用[J].药物生物技术，2009，16（04）：385－387