平面向量在高考试题中的几个难以释怀的“情结”

●

(杭州师范大学附属中学 浙江杭州 31003)

平面向量在高考试题中的几个难以释怀的“情结”

●苏立标

(杭州师范大学附属中学 浙江杭州 31003)

平面向量是高中数学的重要知识点，是沟通代数、几何和三角函数的重要工具.在高考试题中，平面向量试题往往短小精悍，内涵丰富，富有启迪性，特别是浙江省数学高考试题中的平面向量问题更是独树一帜，精彩纷呈，值得我们研究讨论，以供高考复习参考．

1 几何的情结

例1已知a，b是平面内2个互相垂直的单位向量，若向量c满足(a-c)·(b-c)=0，则|c|的最大值是

( )

(2008年浙江省数学高考试题)

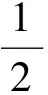
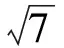
几何特征是向量的重要特征，利用向量的几何特征往往能使问题迎刃而解，向量问题几何化的最常见途径有：构造圆的问题或转化为解三角形问题等．

2 恒等式的情结

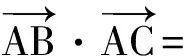
(2012年浙江省数学高考试题)

解法1由余弦定理得

AB2=AM2+BM2-2AM·BMcos∠AMB=

52+32-2×5×3cos∠AMB,

AC2=AM2+CM2-2AM·CMcos∠AMC=

32+52-2×5×3cos∠AMC.

又

∠AMB+∠AMC=180°，

2个式子相加得

AC2+AB2=2AM2+2CM2=2×(32+52)=68,

从而

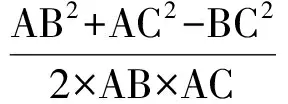
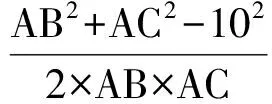
解法2由向量性质知

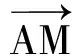
评注比较2种解答方法，利用重要恒等式解答问题，从整体上处理，既避开了繁琐的运算，同时也突出了数学问题的本质，直奔代数运算的主题，过程鲜明，一气呵成，是不错的选择．

( )

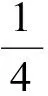
A．∠ABC=90° B．∠BAC=90°

C．AB=ACD．AC=BC

(2013年浙江省数学高考试题)

解设M是BC的中点，则

于是

即

P0M⊥AB.

故选D．

( )

A．C0M⊥AB

B．C0M⊥l,其中l是抛物线过C0的切线

C．C0A⊥C0B

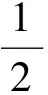
(2013年浙江省高中数学竞赛试题)

其实还可以利用恒等式进行变形应用:把例1中的条件(a-c)·(b-c)=0变为

从而

这就是传说中的圆方程的向量形式,即从代数的视角看向量的几何特征.

3 判别式的情结

(2013年浙江省数学高考试题)

解由条件得

即

从而

即

x2≤4|b|2,

引申已知向量a≠e，|e|=1，对任意t∈R，恒有|a-te|≥|a-e|，则

( )

A．a⊥eB．a⊥(a-e)

C．e⊥(a-e) D．(a+e)⊥(a-e)

(2005年浙江省数学高考试题)

解|a-te|≥|a-e|等价于

(a-te)2≥(a-e)2，

即

t2-(2a·e)t+(2a·e-1)≥0

对任意t∈R恒成立，因此

Δ=(2a·e)2+4(2a·e-1)≤0，

即

(a·e-1)2≤0，

从而a·e=1.故选B.

例5已知平面向量α,β(α≠0,α≠β)满足|β|=1，且α与β-α的夹角为120°，则|α|的取值范围是______．

(2010年浙江省数学高考试题)

分析由向量的几何意义可以把问题转化为解三角形问题,但学生对于构造三角形比较生疏,错误率也较高,因此不妨从代数运算进行考虑,根据题意知

1= |β|2=β2=[α+(β-α)]2=

|α|2+|β-α|2-|α|·|β-α|,

这样就可以得到关于|β-α|的一元二次方程

|β-α|2-|α|·|β-α|+|α|2-1=0

有正实数根，从而

Δ=|α|2-4(|α|2-1)≥0，

向量本身就是数形结合的产物，是衔接代数与几何的纽带,它兼具代数的抽象、严谨和几何的直观、形象等特点，是利用数形结合的一种重要载体.因此向量问题的解决，从理论上来说不外乎有2种途径，即基于几何表示的几何法，以及基于坐标表示的代数法．在具体问题的解答时，要善于灵活运用,学会几何与代数比翼双飞．