对2013年安徽省数学高考理科第18题的进一步探究

●

(德清县第三中学 浙江德清 313201)

对2013年安徽省数学高考理科第18题的进一步探究

●施刚良

(德清县第三中学 浙江德清 313201)

2013年全国高考已经结束，高考试题是高考留给我们的一笔巨大“财富”，可以有效地指导我们今后的教学工作.笔者研究了部分高考真题，其中最令笔者感兴趣的是2013年安徽省数学高考理科试题第18题.

1 试题及答案呈现

(1)若椭圆E的焦距为1，求椭圆E的方程；

(2)设F1,F2分别是椭圆的左、右焦点，P为椭圆E上的第一象限内的点，直线F2P交y轴于点Q，并且F1P⊥F1Q，证明：当a变化时，点P在某定直线上.

(2013年安徽省数学高考理科试题第18题)

图1

解(1)略.

从而

因为F1P⊥F1Q，所以

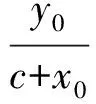
(1)

又点P(x0,y0)在椭圆E上，从而

由式(1)与式(2)知

x0=a2,y0=1-a2,

消去a得

x0+y0=1，

即当a变化时，点P在定直线x+y=1上.

评注此题主要考查椭圆的标准方程，考查学生利用椭圆的标准方程研究相关的几何性质(线线垂直、点在定直线上等)，体现了解析几何的核心思想.学生在处理此题时，关键是怎样将几何条件代数化(如线线垂直转化为斜率之积为-1，点在直线上就是点的坐标满足直线方程等)，当然其中还涉及到一些代数计算,这可能会成为解决问题的“拦路虎”，而这往往是学生解析几何学习中最薄弱的.本题综合考查了学生的计算能力、转化和化归思想、数形结合的意识，能有效地考查学生的数学思维能力.学生一般能很快“上手”，但要深入则“困难重重”，具有很高的区分度，是一道非常成功的试题.

2 试题的一般化

a2+(k2-a2)=k2(k为定值).

记F1,F2分别是椭圆的左、右焦点，P为椭圆E上的第一象限内的点，直线F2P交y轴于点Q，并且F1P⊥F1Q，当a变化时，点P是否还在某定直线上？

下面是具体的探究过程：

从而

因为F1P⊥F1Q，所以

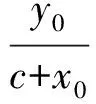
(3)

又点P(x0,y0)在椭圆E上，从而

由式(3)与式(4)知

消去a得

x0+y0=k，

即当a变化时，点P在定直线x+y=k上.

至此，笔者发现“巧合”背后的异常精彩，同时找到试题命制的“源头”：

注特别地，当k=1，即得上述高考试题.

著名数学家波利亚说过：当你找到第一个蘑菇或做出第一个发现后，再四处看看，它们总是成群生长的.在上面的高考试题和命题1的结论中，笔者发现点P都被限制在了椭圆E上第一象限内的点，那么点P是否可以放宽要求,即为椭圆E上的任意点，得到的结论是否与点P为椭圆E上第一象限内的点类似？带着这样的问题,笔者又开始了如下的探究：

从而

因为F1P⊥F1Q，所以

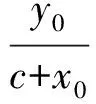
(5)

又点P(x0,y0)在椭圆E上，从而

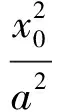
(6)

由式(5)与式(6)知

消去a得

x0-y0=-k，

即当a变化时，点P在定直线x-y=-k上.

同理可得：(1)点P为椭圆E(注：椭圆E的方程与命题1相同)上第三象限内的点，则当a变化时，点P在定直线x+y=-k上；(2)点P为椭圆E(注：椭圆E的方程与命题1相同)上第四象限内的点，则当a变化时，点P在定直线x-y=k上.

将上面讨论的结果叙述如下：

3 试题的类比探究

尽管上面已对高考试题作了一般性的推广，找到了试题命制的本质和源头，但笔者还是感到“意犹未尽”.考虑到圆锥曲线之间往往具有类似的性质，那么上述命题2的结论对双曲线是否也具有类似的性质？通过探究，答案是肯定的.现将结论叙述如下：

注上面的证明过程与椭圆的类似，笔者不再叙述，留给有兴趣的读者进一步探究.

4 结束语

每年的高考试题都是命题者精心打磨的经典之作，一线的数学教师研究高考试题并把它作为教学资源，对于平常的教学和研究具有重要的导向与示范作用.上面笔者通过从特殊到一般的思想方法对高考试题作了推广，并且又通过类比思想将命题2的结论放到双曲线的情形，得到了一些优美的结论.这种探究过程正印证了著名数学家波利亚的话：没有任何一个题目是彻底完成了的，总还会有些事情可以做；在经过充分研究和观察以后，我们可以将任何解题方法加以改进；而且无论如何，我们总可以深化我们对答案的理解.

研而生疑，疑而生思，思而后得.剖析高考试题背后的本质(背景或题源)是破除题海最“给力”的武器，高考试题的本质正是在思维的层层深入中揭开神秘的面纱，使其“原形毕露”，使得我们能够一眼就可以把它“看穿”.在教与学的过程中，教师应该切实加强回顾与反思，使得数学的学术形态转化为学生易于接受的教育形态(让学生也能一眼看出问题的本质，炼就一双“火眼金睛”)，以达到“一题可破万题山，万题可由一题生”的境界.

因此，我们平常应该经常研究高考试题，使其成为我们的一种习惯.对高考试题刨根问底(当然此高考试题必须有一定的研究价值)，“挖掘”其生存的“背景”，让试题“认祖归宗”，有助于我们透过现象看到问题的本质.只有教师自身具有一定的研究能力，学生才能从教师身上感受对问题的研究能力(即“亲其师，悟其道”)，从而提高学生研究问题的能力(这远比学生多做几个题目要“划算得多”)，这是我们数学教学要不懈努力的目标.

[1] 代银，戴晨希.由必然与偶然引发的思考——椭圆的一个性质的探究[J].中学数学：高中版，2013(6):22-23.

[2] 朱贤良.莫让浮云遮望眼，除尽繁华识真颜——对一类高考试题本质的追溯[J].中学数学教学参考：上旬，2013(6)：1-3.