小题目 大思想——2013年浙江省数学高考亮眼小题目漫谈

●

(平湖中学 浙江平湖 314200)

小题目大思想——2013年浙江省数学高考亮眼小题目漫谈

●曲文瑞

(平湖中学 浙江平湖 314200)

2013年高考已经画上了句号，可是我们的研究才刚刚开始,高考试卷中总会有一些题目令人耳目一新,回味无穷.若认真去分析全国各地的高考试题，则会发现有很多好题，而且研究这些典型的、优秀的高考试题也可以为以后的教学指明方向.笔者对2013年浙江省数学高考理科卷进行了研究,感觉其中的几道小题目相当漂亮,符合好题的标准：入口宽阔，解法多样；紧扣概念，体现本质；立意清晰，背景深刻；条件恰当，结论优美；不落俗套，新颖独特；渗透思想，能力到位.可谓小题不小,无论是试题难度、试题新意，还是数学思维能力的考查等，都很有研究价值，蕴含多种数学思想方法.可谓“小题目，大思想”!

1 入口宽泛，解法多样

( )

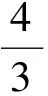
(2013年浙江省数学高考理科试题第6题)

此题主要考查三角函数的定义、同角三角函数的关系、二倍角的正切公式等.此题亲切自然，条件简洁，入口宽，解法多样，内涵丰富.

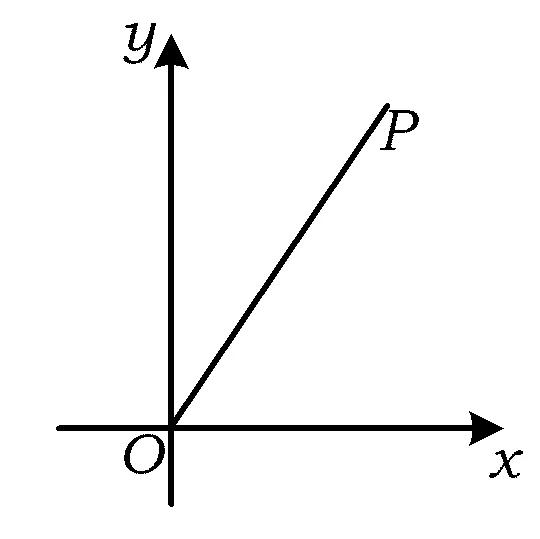
图1

解法1(定义法即坐标法)如图1所示，建立平面直角坐标系，设α终边上任意一点P(x,y)，OP=r,r2=x2+y2.由三角函数定义知

由已知得

化简得

3x2+8xy-3y2=0，

两边同除x2,得

从而

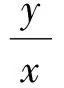
即

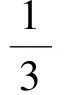
故

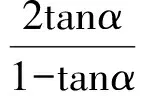
点评解法1紧扣概念，只要学生对三角函数的定义掌握得好，此题就可以很快解决.

解法2(方程思想)由

得

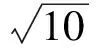
从而

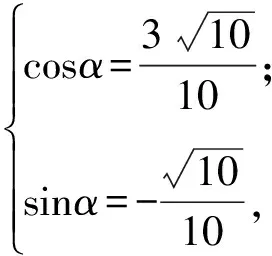
于是

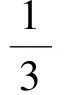
故

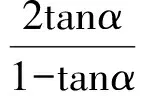
(此题还可以利用

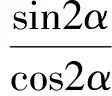
点评解法2主要是从同角三角函数的基本关系入手，构造方程组，直接求解出sinα,cosα.此法学生容易想到.

化简得

3tan2α-8tanα-3=0，

解得

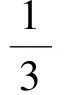
故

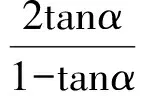
点评解法3利用齐次式可以直接求出tanα，进而求得tan2α.

解法4(引入辅助角)因为

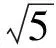
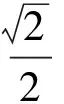
即

或

故

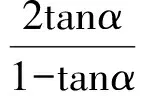
点评解法4主要是利用辅助角公式，解得α与φ的关系，通过φ的正切值求得α的正切值.

( )

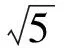
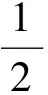
(2008年浙江省数学高考理科试题第8题)

实际上这2道题是同一类型的，2013年的第6题比2008年的第8题更具一般性.

2 立意清晰，背景深刻

( )

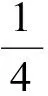
A.∠ABC=90° B.∠BAC=90°

C.AB=ACD.AC=BC

(2013年浙江省数学高考理科试题第7题)

此题主要考查平面向量的数量积、平面向量数量积的几何意义等，立意新颖，背景深刻.

解法1(坐标法)如图2所示，建立平面直角坐标系，设A(0,0),B(4,0)，P0(3,0)，C(x,y),P(x0,0)(0≤x0≤4),则

由已知得

(4-x0)(x-x0)≥x-3，

即

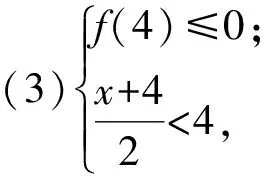
综上所述，x=2，即点C的横坐标为2.又因为AB的中点横坐标也为2，所以AC=BC.

点评坐标法是解决平面向量问题常用的一种方法，易入手，不过最后转化为给定区间上二次函数恒成立问题，讨论起来有点繁琐.

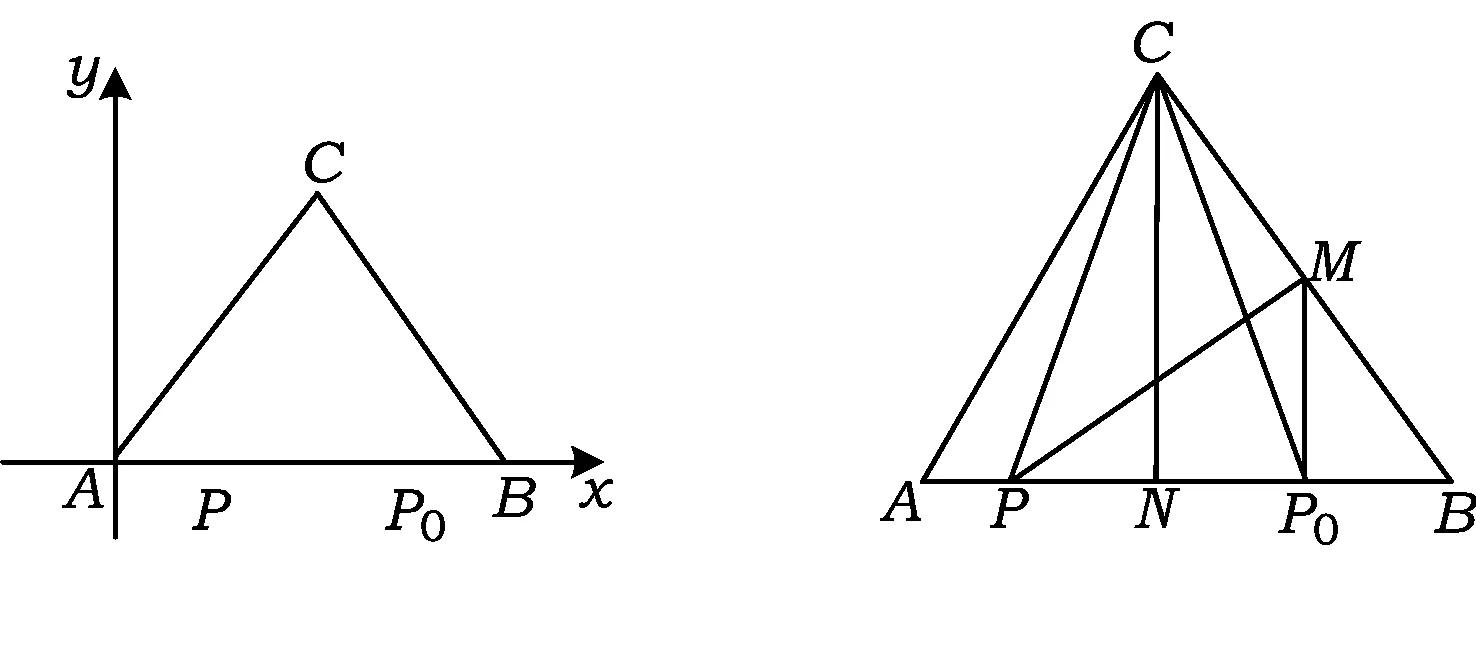
图2 图3

解法2(几何法)如图3，取BC的中点M，AB的中点N，则

即

点评这种数形结合的方法显然比坐标法简单很多，通过图形可以直观感知，能使抽象的数量关系在图形上直观地表达出来，使问题变得简单.

(2012年浙江省数学高考理科试题第15题)

实际上这2道题目的本质也是一样的，都是运用了

其中点M为BC的中点.

3 不落俗套，新颖独特

(2013年浙江省数学高考理科试题第16题)

此题简洁明了,短小精悍,意图清晰,而且通俗易懂，解法多样，入手简单，且蕴含着丰富的思想内涵,符合学生的认知水平.

图4

解法1(坐标法)如图4所示建立平面直角坐标系，设C(0,0)，A(y,0)，B(2,0),则M(1,0).设∠BAM=α，∠MAC=β,则

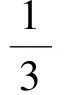
即

点评解法1从同角的三角函数关系及角的代换入手，比较容易想到，符合学生的认知基础.

解法2(构造直角三角形)如图5，设AC=x，BC=2，设∠BAM=α，∠MAC=β，MD⊥AB,则

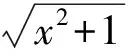
图5

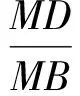
即

点评因为在直角三角形中，正弦值等于对边比斜边，所以很容易想到作垂线，构造直角三角形，把∠BAM放在直角三角形中求解.上述解法2和下面的解法3都是构造直角三角形进行求解.

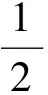
从而

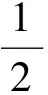
图6

解法4(正弦定理)如图6，设BC=2，AC=x，∠BAM=α，则

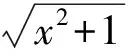
在△BAM中，由正弦定理得

即

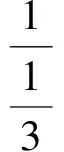
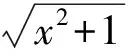
点评已知正弦值、求正弦值，正弦定理也较容易想到，故只需设边长，即可解决.

4 渗透思想，能力到位

(2013年浙江省数学高考理科试题第17题)

此题的立意非常清晰，主要考查了平面向量的基本定理、坐标表示、数量积、几何意义等，而且渗透了多种数学思想方法，能力考查非常到位.

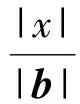
从而

当x≠0时，

故

t∈[0,2].

点评解法2是通过引入参数t建立方程，进而转化为求参量t的最大值的问题.难点也是如何“减元”，如何把多变元问题转化为单变元问题，从而利用一元二次方程有解的思想构造不等式，利用判别式法求出参量t的取值范围.

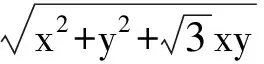
以下同解法1.

点评由平面向量基本定理知,b=xe1+ye2,故|b|=|xe1+ye2|,代入即可.

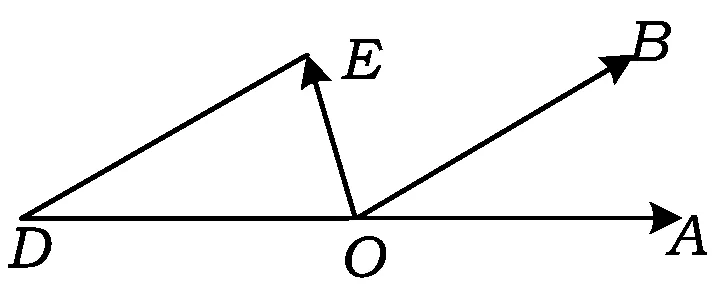
图7

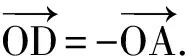
2sin∠OED≤2.

点评解法4利用平面向量的四则运算、平行四边形法则及其几何意义构造三角形，利用正弦定理把边的比转化为角的正弦值之比，突出考查了对问题的转化能力和数形结合的能力.

类似题已知平面向量α,β(α≠0,α≠β)满足|β|=1，且α与β-α的夹角为120°，则|α|的取值范围是______.

(2010年浙江省数学高考理科试题第16题)

实际上这2道题是一样的，都可以利用上述几种方法解决，利用正弦定理尤为简单.

解后反思通过对2013年浙江卷这4道题的研究，不禁会发出“小题不小”的感叹！这些试题蕴含了高中阶段主要的数学思想方法，笔者作了以下反思，为今后的教学尤其是高三数学复习作准备：

(1)高三复习时应由“双基”到“四基”转变.

“双基”：基础知识、基本技能；“四基”：基础知识、基本技能、基本思想、基本活动经验.

从以上的4道题目我们也可以发现，高中阶段重要的数学思想方法的四大育人功能在2013年浙江省数学高考理科卷中都有体现.由此可见，在教学中关注数学思想方法、在教学中渗透数学思想方法十分重要.当然，这些数学思想不是孤立的，而是互相渗透的，有意地去体会并运用这些数学思想，才能抓住解题的核心和本质，站得高才能看得远，才会起到事半功倍的作用.

(2)研究高考试题，探究试题背景，提升思维能力.

在课堂教学中，以高考试题为载体，可以有效提高高三复习课效率.因为高考试题是命题者潜心研究、匠心独运、精心设计的精品，具有很高的练习、研究价值.近几年，全国试题和部分省市自主命题更是让试题如串串珠玑，精彩纷呈，构筑起一座丰厚的试题宝库.将高考试题恰当地引入高中数学的教与学，通过高考试题的引领，让学生注重解题的通性通法，淡化特殊技巧，注意数学概念、数学本质和解决数学问题的常规方法.通过一题多解、多题一解，多角度揭示问题本质，拓宽解题思路.这样，不仅可以激发学生的学习和研究兴趣，而且可以达到培养学生思维能力的目的,从而提升教学的有效性.如本文中的这4道题目，其中有3道题目是与前几年浙江卷中的试题背景相似.可见，研究高考试题意义重大.

近几年浙江省的高考试题加大了对学生探究能力、创新能力、思维能力的考查，“题海战术”收效甚微.因此，若教师在平时的教学中能对这些构思巧妙、内涵丰富的高考试题进行精心研究，探究其背景，并进行适当拓展和创新，可以更好地理解课程标准、掌握命题趋势、把握高考的重难点，从而更好地提高备考质量、复习效果.