从分式运算对理科学生的解题要求谈起——对浙江省数学高考试题的几点思考

●

(杭州市第十四中学 浙江杭州 310006)

从分式运算对理科学生的解题要求谈起——对浙江省数学高考试题的几点思考

●夏霖马茂年

(杭州市第十四中学 浙江杭州 310006)

2013年高考结束，关于数学高考试题的各种分析铺天盖地，有的挖掘试题背景给出精彩“秒杀”解法，有的借助数学软件从直观的角度寻求解法，诚然上述研究作为教研活动值得提倡，能够开拓教师教育教学的思路.笔者认为，教师不仅要站在“山顶”高屋建瓴地给“山下”的学生指点江山，更应走到“山下”，给学生指一条路，并且陪着学生一起“上山”，让学生能够自己到“山顶”领略无限风采.对于考生而言，在紧张的考试过程中，往往很难实现“秒杀”.笔者试着以一名普通考生的心境做完2013年浙江省数学高考卷，发现本着一颗平常心，不追求奇思妙解，踏踏实实地从题意出发，走平常路，也能得到不错的成绩.

本文仅以理科卷中能用到分式运算的试题为例，因为通观文、理卷，笔者深深感触到:文科和理科对于分式运算的要求大为不同，粗粗算来理科卷中涉及分式运算的有以下几题：第6,16,17,19,21题，而文科卷仅一题.本文中笔者列举的处理分式的方法都是基本方法，于学生而言容易上手，在有限的考试时间内不必花费大量时间寻找解题思路，稳扎稳打即可收获成功.

(2013年浙江省数学高考理科试题第6题)

即

从而

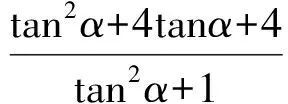
可化为

3tan2α-8tanα-3=0,

从而

因此

注解法1是处理分式“齐次式”的常用方法，分子、分母同除以某一项，以统一变元.

类似地,我们还可以处理例2：

(2013年浙江省数学高考理科试题第17题)

故

从而

又

sin2α+cos2α=1,

得

(k2+1)cos2α=1,

即

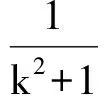
故

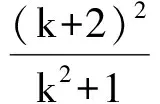
从而

3k2-8k-3=0,

得

则

(2013年浙江省数学高考理科试题第19题)

解由题意得

即

3a+6b+9c=5(a+b+c),

从而

2a-b-4c=0.

(1)

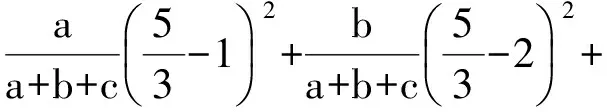
从而

4a+b+16c=5(a+b+c),

即

a+4b-11c=0.

(2)

由式(1),式(2)解得

a=3c,b=2c,

从而

a∶b∶c=3∶2∶1.

(2013年浙江省数学高考理科试题第16题)

解设BM=CM=x,AC=y,则

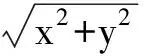
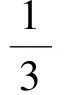
在△ABM中，由余弦定理得

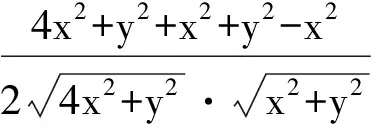
从而

2x2=y2,

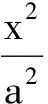
(2013年浙江省数学高考理科试题第21题)

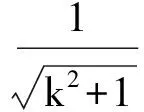
(4+k2)x2+8kx=0,

故

从而

设△ABD的面积为S，则

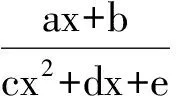
的形式，然后用基本不等式或者“打勾”函数来处理.

教学建议分式运算这一内容在高中数学课本中没有单独地成章成节，它分布在函数值域、函数单调性、三角函数求值、方程根的分布、不等式的证明等问题中，从高一新课到高三复习都占有一席之地.在教学中，教师应对那些符合学生思维习惯、认知基础的通解通法予以高度重视，培养学生对分式运算类型的辨析及快速准确的应对能力.对于超出学生思维习惯、认知基础的特殊技巧，教师可以启发式讲授，但要深入挖掘其合理性、必要性，力求自然、和谐、水到渠成.