65 t/h高低差速循环流化床流动特性模拟

刘洪鹏，肖剑波，李惟毅，陈冠益，王 擎

（1天津大学环境科学与工程学院，天津 300072；2东北电力大学能源与动力工程学院，吉林 吉林132012；3天津大学机械工程学院，天津 300072）

高低差速循环流化床系江西江联能源环保股份有限公司引进德国高低床技术发展而来[1]，属于内循环流化床的范畴，是在鼓泡床和高倍率循环流化床磨损严重和差速床沸腾锅炉技术的背景下开发出来的。高低差速循环流化床有埋管磨损轻、燃料在床内停留时间长、污染物排放少和燃料适应性广等优点，现已广泛应用到能源、化工等领域。

研究高低差速循环流化床气固两相流动特性，对锅炉的结构及运行优化和大型化是很有必要的，然而对于大型的工业化内循环流化床来说，进行详细的气固流动特性的试验研究是非常困难的，随着计算机性能的不断增加，基于计算流体力学的数值方法得到长足发展，并在循环流化床等复杂多相流系统结构和运行优化以及大型化中起到了重要的作用[2]。Yu等[3]运用基于颗粒动力学理论的欧拉双流体模型对差速流化床进行了二维模拟，研究了表观气速、颗粒初始填充高度、布风板倾斜度以及埋管束等结构和运行参数对颗粒循环率的影响。田凤国等[4]采用离散单元法（DEM）数值模拟与试验台相结合的方法系统研究了内循环流化床的气固流动特性。此外，钊丽等[5]针对差速循环流化床锅炉特有的结构，采用小室模型对炉内煤的燃烧及其物理、化学反应过程进行了相应的仿真计算。

本文作者运用基于颗粒动力学理论的欧拉双流体模型对一台65 t/h高低差速循环流化床炉内流动特性进行二维数值模拟。在欧拉双流体模型中分别采用单粒径固相模型和多粒径固相模型，并对模拟结果进行对比分析。分析了炉内颗粒速度分布、压力分布和颗粒浓度分布，研究结果为更深入了解高低差速循环流化床的气固流动特性、优化设计及大型化提供了理论依据。

1 模拟条件

1.1 物理模型与网格划分

物理模型为JG-65/3.82-M型高低差速循环流化床锅炉炉膛部分[6]，炉膛的核心是密相区，密相区由主床和左、右副床组成，也称为高速床和低速床。高速床比低速床低 400 mm，并由隔墙分开，隔墙下部设有回流孔。燃料由两侧墙给料口进入主床，在主床内物料按不同粒径自动分离，粗颗粒集中在低层主床上，细的部分趋于上层的副床上，由于分离后的副床上床料平均粒径比给料的平均粒径小，因此副床的流化风速可比主床小1～1.5倍，高、低速床的不同流化风速形成了床料的内循环，强化了床内物料横向混合，延长了给料在床内的停留时间。此外，小的粒径和低流化风速使副床上埋管受热面的磨损程度显著减轻。整个计算区域均采用四边形结构化网格划分，高低差速循环流化床二维物理模型如图1所示。

图1 高低差速循环流化床二维模型

1.2 数学模型

气固两相流动模型采用基于颗粒动力学理论[7]的欧拉多相流模型、湍流模型、气固曳力模型分别采用 RNGk-εper phase[8]模型和 Gidaspow 模型[9]。以计算流体动力学软件Fluent为计算平台。采用控制容积法离散控制方程，以一阶迎风获得差分格式控制容积界面物理量，流体压力-速度耦合基于Simple算法。

1.3 参数设置

欧拉双流体模型中气相为基本项，单粒径固相模型粒径为0.5 mm，多粒径固相模型颗粒粒径分别为0.1 mm、0.5 mm和3 mm。气相密度和黏度按床温为850 ℃对应的值来进行设定。气固两相物性参数、初始和边界条件分别见表1和表2。在壁面处，气相选择无滑移边界条件，固相选择部分滑移条件，镜面反弹系数取 0.6[10]。颗粒碰撞恢复系数表征颗粒间碰撞后动能恢复程度，多数研究者选取 0.9～0.99[11-12]，本研究选取0.95。时间步长取0.001 s，计算时间为10 s。

1.4 二次风口矫正

计算选用的模型不涉及燃烧，炉内温度场简化为单一分布，即炉内温度统一为T1。而在实际运行条件下，锅炉二次风在射入炉膛前，其温度为空气预热器后热空气温度Tk，二次风在喷入炉膛后，其温度骤升并迅速接近炉内温度T1，体积也相应地发生剧烈膨胀。由于模型中炉内简化为单一温度分布，因此在保证同样的二次风量的情况下，其二次风速将是实际的T1/Tk倍。但实际上二次风进入炉膛后，其体积扩散不仅是轴向膨胀增加风速，还包含径向扩散。本研究运用二次风口矫形模化方法[13]。将二次风口放大为实际尺寸的倍。其主要原理是模拟在处理二次风进入炉膛后因温度骤升而造成体积膨胀的影响时，保证了二次风与炉膛中心风的动量比相等。

表1 气相和固相特性参数

表2 初始条件和边界条件

2 结果与分析

2.1 模型验证

密相区高、低速床内各布置有一个压力测点，其瞬时压力随时间的变化如图2和图3所示。所选模型计算的平均压力值与实测平均压力值的误差对比如表3所示。

由图2、图3及表3可知，单粒径固相模型的模拟结果更接近床内的实测平均压力值，误差在工程允许范围内，多粒径固相模型模拟结果误差较大。其可能的原因是多粒径计算方法中所用的 Schillernaumann曳力模型不能精确描述不同粒径颗粒间的相互作用力，该模型还有待进一步完善。另外，低速床的模拟误差较高速床大，原因是忽略了埋管。

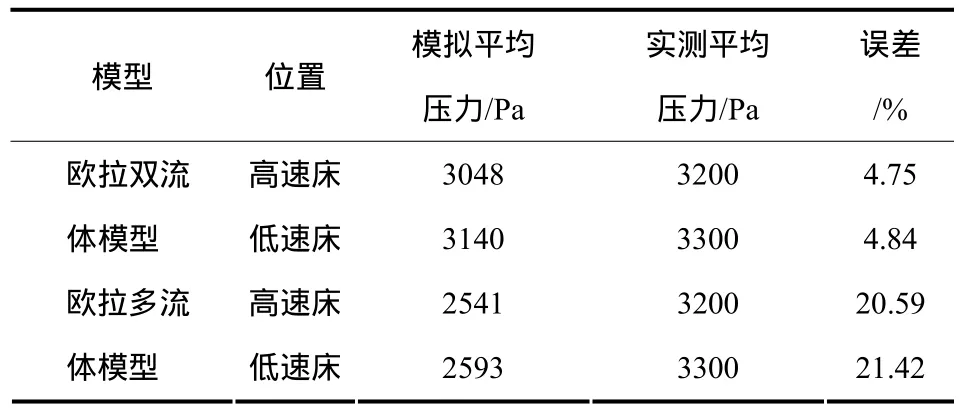
表3 模拟值与实测值误差对比

2.2 颗粒浓度及压力分布

图4为高低差速循环流化床密相区在不同时刻的颗粒浓度分布。初始堆积床料在高、低速风的吹动下开始流化，初始时刻小部分颗粒通过回流孔由高速床进入到低速床，大部分颗粒像涌泉一样翻腾到高速床中上部，此时由于颗粒从小截面的高速床进入到大截面流场，颗粒急速回落，小部分又回到高速床，进而又不断被高速风吹动涌起，大部分溢流到低速床，并从低速床底部重新回到高速床，在高速风的吹动下，重新被流化起来，进行着周而复始的循环。

图5为流化开始阶段高低差速床密相区压力分布特性。结合颗粒浓度分布特性可以看出，颗粒由于高速风的带动溢流于高速床表面，造成此处颗粒浓度较高，则压力较高；而低速风带动的床面较低，此处颗粒浓度较低，则压力较低，形成了顶部从高速床到低速床的压力差，此压力差使颗粒涌流向低速床；低速床颗粒浓度的增加形成了密相区底部回流位置从低速床到高速床的压力差，此压力差使颗粒从低速床回流到高速床，进而形成了密相区周而复始的内循环流动。高、低床间形成的压力差为密相区的内循环流动提供了动力，同时反映了内循环流动的机理。

2.3 粒径分布

图6为分别运用单粒径模型和多粒径模型所模拟的颗粒粒径分布特性。由图6(b)可知，0.1 mm颗粒主要分布在高、低床上部区域及稀相区，且大部分颗粒随流化风吹出炉膛；图6(a)和图6(c)显示0.5 mm颗粒主要分布在左右副床上，两种模型所预测的结果是一致的；由图6(d)可知，3 mm颗粒主要分布在主床上。稀相区的颗粒浓度分布受二次风影响较大，在二次风两侧形成低颗粒浓度区，但随着炉膛高度增加，颗粒浓度分布趋于均匀。在欧拉双流体模型中采用多粒径固相能够预测实际锅炉宽筛分颗粒的分布特性，但与单粒径相比其准确性还有待提高。

2.4 速度分布

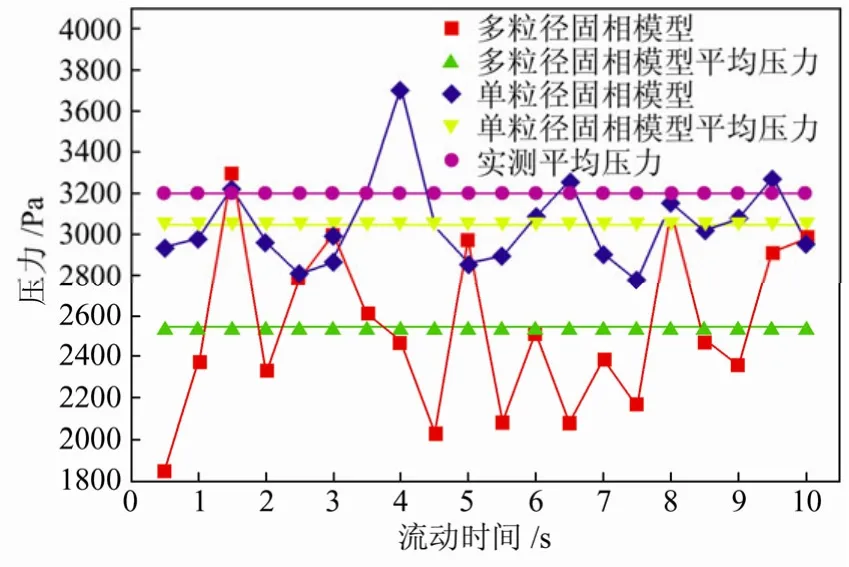
图2 高速床测点瞬时压力随时间的变化

图3 右低速床测点瞬时压力随时间的变化

图4 密相区不同时刻的颗粒浓度分布

图5 高低差速床密相区压力分布特性（单位：mm）

图6 粒径分布

图7～图10为密相区0.5 mm颗粒内循环流动的速度分布特性。由图可见，在密相区回流孔位置（H=600 mm），颗粒横向速度左低速床为正，右低速床为负，这说明颗粒沿回流孔从低速床回到高速床；颗粒纵向速度在低速床靠近炉墙边壁的位置为负，靠近回流孔位置为正，这说明涌入的颗粒沿低速床边壁回流到高速床且部分颗粒在靠近回流孔位置重新流化起来，从而在低速床中部位置有旋涡存在，这与矢量图中的结果是一致的。

图7 颗粒横向速度矢量图

图8 颗粒纵向速度矢量图

图9 颗粒横向速度随炉膛高度变化曲线图

图10 颗粒纵向速度随炉膛高度变化曲线图

在密相区中部位置（H=700 mm、750 mm、850 mm），颗粒横向速度值较小且基本在零附近，再次说明此位置有旋涡存在。

在密相区隔墙顶部位置（H=1300 mm），颗粒横向速度左低速床为负、右低速床为正，颗粒纵向速度为负，且在靠近炉墙的区域数值较大，这说明颗粒沿炉墙边壁由高速床涌入低速床。颗粒在高速床的横向速度几乎为零，纵向速度为正且数值较大，这说明由低速床回到高速床的颗粒在高速风带动下重新流化起来，此外，高速床右侧纵向速度较低，原因是受返料影响，增加颗粒内循环量，使此处颗粒浓度较高，流化效果较左侧稍差。

3 结 论

（1）基于颗粒动力学理论的欧拉双流体模型能够较好地预测高低差速循环流化床的气固两相内循环流动特性。

（2）单粒径固相模型较多粒径固相模型的模拟结果更接近床内的实测平均压力值。

（3）在欧拉双流体模型中采用多粒径固相能够模拟实际锅炉宽筛分颗粒的分布特性，0.1 mm颗粒主要分布在稀相区，0.5 mm颗粒主要分布在低速床上，3 mm颗粒主要分布在高速床上，但与单粒径相比其准确性还有待提高。

（4）模拟得到的速度和压力分布能够解释密相区颗粒内循环的机理，高、低速床间形成的压力差为密相区内循环流动提供了动力。

[1] 桂北芳. 高低差速锅炉在设计运行中关键技术问题探讨[J]. 工业锅炉，2006（3）：18-22.

[2] Schwarz M P. The role of computational fluid dynamics in process modeling[C]//6th AusIMM Extractive Metallurgy Conf，1994：31-36.

[3] Feng Yuqing，Tim Swenser-Simth，Witt Peter J，et al. CFD modeling of gas–solid flow in an internally circulating fluidized bed[J].Powder Technology，2012，219：78-85.

[4] 田凤国，章明川，范浩杰，等. 内循环流化床颗粒流动特性的数值模拟[J]. 上海交通大学学报，2007，41（3）：347-351.

[5] 钊丽，徐向东. 差速循环流化床的数学模型研究[J]. 清华大学学报：自然科学版，1998，38（4）：72-75.

[6] 陈玉村，陈晗霞，余更孙. 浅谈65t/h燃低劣油页岩差速流化床锅炉的设计[J]. 工业锅炉，2008（5）：15-17.

[7] Ding J，Gidaspow D. A bubbling fluidization model using kinetic theory of granular flow[J].AIChE Journal，1990，4：523-538.

[8] Hartge Ernst-Ulrich，Ratschow Lars，Wischnewski Reiner，et al.CFD-simulation of a circulating fluidized bed riser[J].Particuology，2009，4：283-296.

[9] Gidaspow D. Multiphase flow and fluidization [M]. San Diego：Academic Press，1994.

[10] Zhang Nan，Lu Bona，Wang Wei，et al. 3D CFD simulation of hydrodynamics of a 150 MWe circulating fluidized bed boiler[J].Chemical Engineering Journal，2010，162（2）：821-828.

[11] Taghipour F，Ellis N，Wong C. Experimental and computational study of gas-solid fluidized bed hydrodynamics[J].Chemical Engineering Science，2005，60（24）：6857-6867.

[12] Cloete S，Amini S，Johansen S T. A fine resolution parametric study on the numerical simulation of gas-solid flows in a periodic riser section[J].Powder Technology，2011，205（1-3）：103-111.

[13] 王超，程乐鸣，周星龙，等. 600MW超临界循环流化床锅炉炉膛气固流场的数值模拟[J]. 中国电机工程学报，2011，31（4）：1-7.