被动式DMFC气泡行为的实验研究和数值模拟

张飞翔，齐 亮，姚克俭

（浙江工业大学化学工程与材料学院 绿色化学合成技术国家重点实验室培育基地，浙江 杭州 310014）

直接甲醇燃料电池（DMFC）是一种将化学能直接转化成电能的发电装置，具有环境友好、效率高的优点，日益受到各国政府和企业的重视[1-2]。DMFC根据电池供液方式的不同分为主动式和被动式。被动式DMFC结构更为简单，由于没有阳极燃料循环系统，更易于微型化，用于像笔记本电脑、手机和个人电子助手等电子设备，作为便携式电源的最佳选择之一[3-4]。在阳极通道中，甲醇溶液经多孔扩散层到达催化剂层，在催化剂层反应产生的CO2气体会占据扩散孔道，对甲醇渗透产生影响，阻碍反应的进一步进行，因此能否及时排出对电池性能的提高具有重要影响[5]。

目前一些学者利用可视化技术对 DMFC内气泡的产生过程进行了大量的实验研究，考察了在不同条件下产生气泡的形状、脱离周期及脱离大小[6-7]，但由于实验过程破坏了电池原有结构，对于微尺度下气泡产生过程的观察受到诸多条件的限制，因此有必要采用数值模拟的方法对其进一步研究。Delnoij等[8]运用欧拉制-拉格朗日模型描述了溶液中弹状流的流体动力学。Lee等[9]运用多种流体模型对水平表面生长的气泡进行了数值模拟。Xu等[10]运用有限元法对球形气泡的生长过程进行了数值模拟。Gerlach等[11]结合 level-set和 VOF（volume of fluid）方法模拟了轴对称坐标下气泡的形成、脱离及上升过程。这些模型所研究的体系相对较大，对微细通道气泡产生过程没有研究。

何健烽等[12-13]对气泡及气液两相流进行了较为深入的研究，工作主要集中在主动式DMFC内的气液两相流和流道结构优化，对被动式电池内气泡生长脱离机理及气泡在孔口的聚并过程研究较少。本文作者利用计算流体力学，采用VOF数值模拟和可视化实验对气泡生长及脱离过程进行研究。

1 模型的建立

1.1 模型假设

在数值模拟中，对模型作如下假设：①气泡在饱和甲醇溶液中生成，不考虑CO2溶解过程；②流体不可压缩，气相与液相之间没有穿插；③所有流动认为是层流流动；④孔口处气速较低，形成的气泡以鼓泡的形式进入通道内；⑤被动式低电流密度放电过程，气泡直径相对较小，忽略壁面影响；⑥甲醇浓度及温度恒定。

1.2 模型的建立

采用体积函数模型来描述阳极通道内的气液两相流，通过计算每一个控制体积内每一相的体积分数来捕捉相界面，在每个控制体积内，所有相的体积分数之和为 1，所有变量及其属性区域被各相共享并且代表了容积平均值。因此在任何给定单元内的变量及其属性或者纯粹代表了一相，或者代表了相的混合，这取决于体积分数值，即可能出现以下3种情况。

（1）αq=0，第q相的流体在单元中是空的。

（2）αq=1，第q相的流体充满整个单元。

（3）0 ＜αq＜ 1 ，单元中包含q相流体和其它一相或者多相流体的界面。

层流状态下的非稳态气液两相流动的控制方程可以表述如式（1）～式（6）[14-15]。

式（3）中的动量源项是由表面张力和壁面黏滞力产生的。式（4）表示在一个单元网格内气相和液相之和为 1，式中气液两相密度和黏度分别乘以各自的体积分率就是每个控制体内的密度和黏度。计算过程中对源项处理采用 CSF（Continuum Surface Force）模型，如式（7）[16]。

在这种处理方法中，源项被认为是表面张力σ和表面曲率k的函数，曲率k与壁面的表面张力密切相关，可以根据如式（8）过程计算。首先定义n为第二相的体积分数在α2液面法线上的梯度，如式（8）。

其次定义曲率k为单位法线n的散度，如式（9）。

如果用θw表示壁面的接触角，则与壁面相邻 的微元体内液面的单位法线长度可以定义为式（10）。

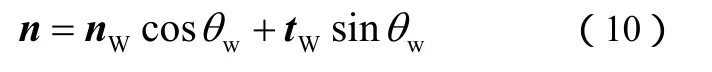
式中，Wn和Wt分别是在垂直于壁面方向和平行于壁面方向的单位向量。根据这种计算方法可以计算出气液交界面上每一点的曲率。

1.3 计算区域及离散化方法

图1 研究的流体轮廓和坐标系

图1为气泡生长过程图。Zmax为气泡的纵向高度，Zmax和气泡最大宽度的比值定义为气泡纵横比，O点处是大小为0.2 mm的孔口。阳极通道充满静态甲醇水溶液，阳极通道尺寸为5 mm×12 mm。CO2气体从扩散层孔道进入阳极通道，为使结果精确采用较小的网格，利用Gambit把计算区域进行网格划分，网格为20 000～28 000时计算结果不再跟网格数有关，所以本文模拟采用不低于28 000网格数的划分方法。液相C=1 mo1/L甲醇水溶液，采用非稳态算法，温度T=25 ℃，表面张力σ=0.070 66 N/m。

气泡的对称轴采用对称性边界条件。

进口采用速度进口条件，气速ug=0.2 m/s。

出口采用压力出口条件，出口压力一个标准大气压=101.325 kPa。

设置压力速度耦合对应的求解方法为PISO，离散化方法对应的压力出口为Body Force Weighted，求解动量方程为二阶迎风格式，时间步长设为1×10−5s。所用计算机为2G内存，AMD 4000+双核处理器，处理时间为4～10 h。

2 实验装置及实验方法

实验装置及设备如图2所示。本实验系统由可视化实验段、气源装置以及高速摄影仪组成。可视化实验段采用有机玻璃板加工制成，气体由蠕动泵带动注射管产生，通过尺寸为160 mm×5 mm×5 mm的通道，缓冲后进入0.2 mm×0.2 mm×3 mm的微细通道垂直注入甲醇水溶液中。实验过程中，用蠕动泵调节气体的进气流量，把光源垂直照射到孔口，调节光源强度，以便能清晰看到孔口处生成的气泡，采用高速摄影仪拍摄气泡生成过程，考察气体流速及甲醇浓度对气泡脱离行为影响。

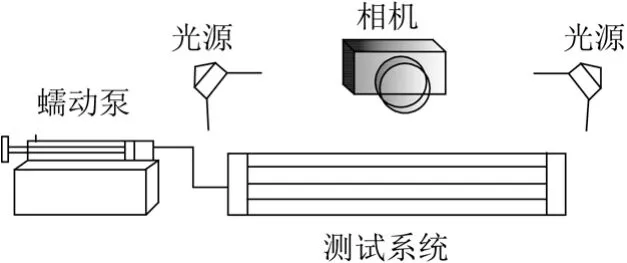
图2 实验流程图

3 结果与讨论

3.1 气泡在扩散层表面的生长脱离过程

气泡生长过程数值模拟结果如图3所示，接触角为40°，液相为1 mol/L甲醇水溶液，气速为0.2 m/s，孔口大小为0.2 mm。

采用形变和大小表征气泡的生长情况。从图3可见，气泡初始状态接近于球形，随着气体逐渐注入，直径不断增大，气泡纵向生长速度大于横向生长速度，形状变的不规则。对不同时刻气泡内的压力进行记录发现，压力会随着气泡直径的增大而减小，这是由于随着气泡直径的增大，气泡受到附加压力减小的结果。

图4为气泡生长至脱离过程纵横比变化曲线，由图可见，气泡生长初始阶段纵横比大于 1，生长至脱离过程，纵横比不断增大，脱离瞬间达到最大值。受浮力影响，脱离扩散层垂直上升过程中，气泡由近似球形迅速变为椭球形，纵横比在压力作用下迅速减小。定义气泡脱离时间为气泡刚鼓出扩散层到完全脱离所用的时间，气泡脱离直径为脱离时刻气泡横向最大宽度和纵向长度的平均值。

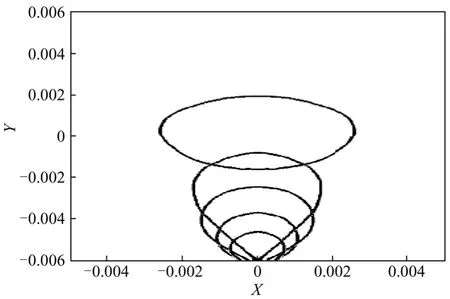
图3 水平孔口气泡的形状图

图4 气泡生长脱离过程的纵横比

图5 气泡在不同时刻的直径和接触环直径

图6 气泡在不同时刻的表面张力和浮力

图5为气泡生长过程中的直径及接触环直径的关系曲线，图6是根据气泡直径和接触环直径得到的浮力和表面张力关系曲线。

从图5、图6中可见，0～0.1 s气泡与扩散层之间的接触环直径随气泡直径的增大而变大，开始浮力小于表面张力，气泡被束缚在扩散层的表面。0.1～0.25 s，浮力作用使气泡上升，气泡与扩散层之间的连接力（表面张力）使气泡尾部附着在扩散层上，浮力和连接力作用的结果使气泡纵向被拉长，同时动能产生的动压也会影响到气泡的形状。0.25 s后气泡与扩散层分离，其尾部气液界面受液体剪切力作用，加上垂直向上的浮力使气泡脱离速度加快。

图7是水平孔口处气泡的生长过程，甲醇水溶液为1 mol/L，CO2进气流量为0.2 m/s。

图7为可视化实验过程的气泡形状图，由图可见，开始生长时气泡附着在扩散层表面呈球形，生长过程中接触直径与气泡直径比值逐渐减小。随着气体不断注入，气泡在浮力和尾部接触力的共同作用下拉长。随着气泡变大，浮力作用不断增强，其尾部和扩散层的接触面积不断减小使得气泡脱离扩散层。气泡从鼓出到脱离只需要0.015 s，远小于气泡的孕育时间，就是说气泡刚鼓出孔口时压力最大，气泡生长过程中其内部压力减小使得气体膨胀，与模拟得到的结果相符合。

图7 实验过程中气泡的形状图

3.2 倾斜扩散层表面对气泡生长脱离影响

在被动式DMFC便携式应用中，其方位状态可能会不断改变，电池倾斜角度不同会对气泡脱离产生影响。方位不同，气泡受到外力的作用效果会随之改变，导致浮力对气泡脱离行为产生不同的影响，因此研究气泡在不同倾角扩散层孔口处的生长脱离行为尤为重要。

图8模拟比较了气泡在不同倾斜扩散层表面的脱离行为，其中孔口直径为0.2 mm，气速为0.2 m/s。由图可见，在气泡生长初期，气泡成半球形生长。当气泡长大到一定程度后，受浮升力影响，开始非对称生长，左侧气液接触角缓慢增大，右侧气液接触角减小。气泡并非相对于Y轴对称形成，而会向扩散层倾斜方向滑移。倾斜角度越大，气泡左右两边受力就会越不平衡，这种不平衡作用力作用的结果使得气泡右边与扩散层的接触面积增大，气泡左边与扩散层的接触角接近90°。气泡在浮力作用下垂直生长，在倾斜方向上产生一个分力，其随着倾斜角度变大而增大，用来克服气泡与扩散层之间的摩擦力。

由图9可知，随着倾斜角的变大，气泡的脱离直径和脱离时间减小。其原因主要是气泡生长过程中，液体浮升力为影响气泡生长的主要作用力，随着毛细管倾斜程度增大，浮升力的作用使得气泡与孔口左侧脱离时间提前，从而使气泡生长脱离周期变小，气泡脱离体积变小。倾斜状态下，浮升力的作用使得气泡左侧接触角增大，右侧接触角减小，从而使气泡所受到的表面张力在竖直方向上减小，因此脱离毛细管所需的浮升力变小，气泡的脱离直径减小。浮力在倾斜表面上的分力会随着角度的增大而增大，在浮力作用下，气泡很容易在倾斜的扩散层表面滑动，其结果使得气泡很快脱离。

图8 气泡在倾斜扩散层上脱离过程的模拟

图9 孔口方式对气泡生长的影响

图10为气泡在倾斜扩散层表面生长的实验研究，倾斜角θ=36°，进气速度0.2 m/s。

从图10可见，扩散层表面倾斜时，气泡生长的同时向扩散层倾斜方向移动，受力不平衡的结果使气泡以更小直径脱离。气泡和扩散层的接触面积主要在孔道口右边。当电池阳极扩散层的孔口向下时，气泡会在浮力作用下紧贴扩散层表面生长，倾斜角度越小生成的气泡直径就越大，这样不利于气泡及时脱离。因此孔口方位对气泡脱离影响较大，模拟和实验得到了相似的结论。

图10 气泡在倾斜扩散层上脱离过程示意图

3.3 CO2气速大小对气泡生长脱离影响

考虑到电池可能在不同的放电电流下工作，因此产生CO2气体的速率有所不同，为了研究不同气体流量对扩散层孔口的气泡生长及脱离影响，数值模拟了不同气速下气泡生长过程。图11为不同气速与脱离直径关系曲线，孔口直径为0.2 mm。

由图11可知，随着CO2气速的增大，单位时间内进入气泡的气量增多，浮力的作用还没来得及使气泡脱离，气泡迅速膨胀，脱离直径增大；同时脱离时间减小，气泡生成频率增大，纵横比变大。

孔口气速大小判断的依据是孔口产生的前级气泡是否被后续气泡所聚并，若发生聚并，则表明气速较大；反之则表示气速较小[17]。基于该判断依据，推导临界流速uoc，得到式（11）。

对于被动式DMFC甲醇浓度1 mol/L而言，式（11）可以写作uoc= 0.27d0-1/6，即孔口气流的临界气速与孔口直径d0有关。当d0=0.2 mm时，uoc=1.1 m/s。

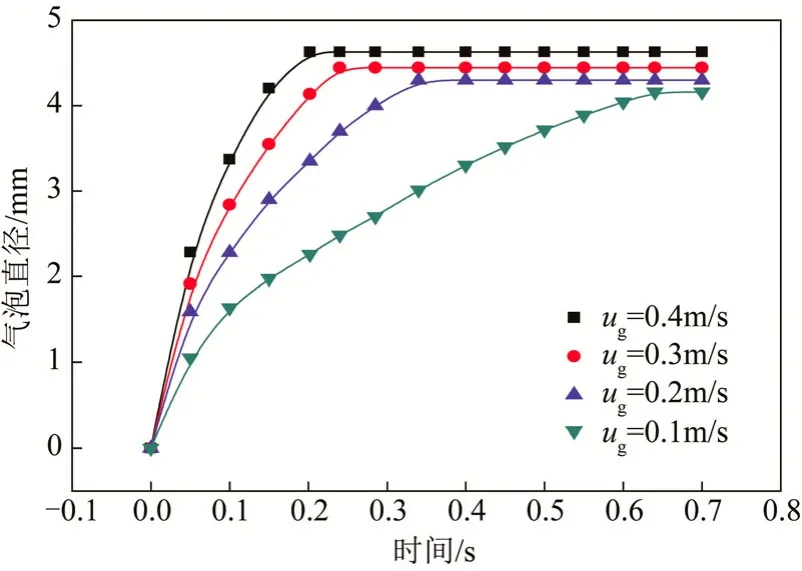
图11 CO2气体流速对气泡生长的影响

图12为不同气速下气泡纵向高度示意图。由模拟结果可知：气速由0.4 m/s增加到1.1 m/s的过程中，在0～0.2 s时间内，气泡的纵向高度由5.5 mm逐步增大到11.5 mm。气速越大，气泡的纵向生长速度越快；脱离过程中，其尾部会和孔口形成一个颈部结构，气速越大，该结构维持时间越长。

气泡二次融合过程实验研究如图13所示，气速为1.1 m/s。

由图13可见，气泡在入流气体惯性力作用下纵向生长，而已经脱离的气泡由于不受惯性力作用，会导致其上下震荡，尾部拖长，结果使得前后两个气泡第一次融合，构成一个连续的气相，形成更大的气泡。与此同时气泡刚脱离孔口时，由于突然断开的气相使得气泡尾部区域压力迅速减小。在该压力作用下，已经脱离的气泡会与扩散层形成的小气泡发生二次融合或多次融合。实验结果验证了模拟的可靠性。

3.4 甲醇浓度对气泡生长脱离影响

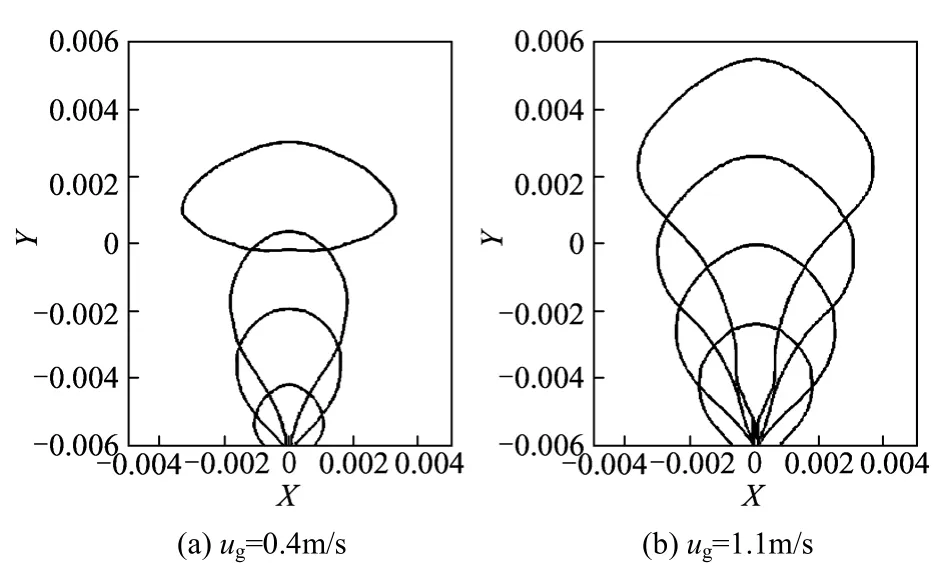
图12 不同气速-纵向高度关系图（θ=50°）

图13 气泡二次融合过程示意图（1 mol/L）

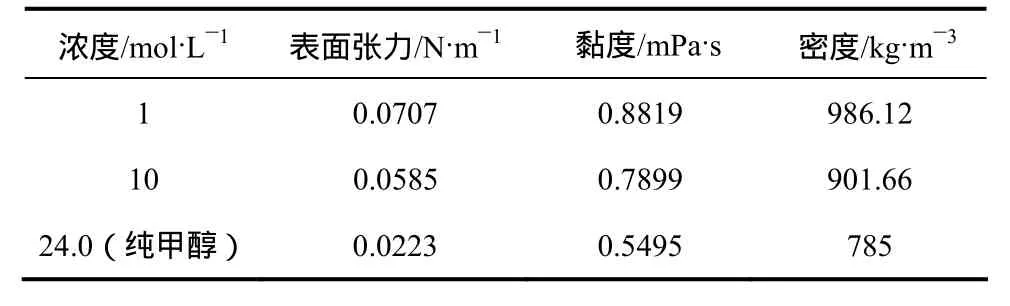
表1 25 ℃下不同浓度甲醇溶液的物理性质

DMFC在使用的过程中甲醇浓度会不断发生变化，溶液物性的改变会对气泡的生长脱离产生影响，本节考察甲醇浓度对气泡的影响。表1表示25 ℃时不同浓度甲醇溶液表面张力、黏度和密度的参数。

本文通过数值模拟，研究气泡在不同浓度甲醇溶液中的生长脱离行为，模拟孔口大小为0.2 mm，气速大小为0.2 m/s。

图14为0.4 s时刻，不同甲醇浓度气泡脱离后的几何示意图。由图14可见，随着甲醇浓度的升高，气泡生长脱离周期变短，脱离直径变小；气泡在 1 mol/L甲醇水溶液中脱离直径较大，在24 mol/L甲醇溶液中脱离直径最小。气泡脱离后，由于气液界面断开使得气泡纵向收缩，在不稳定流场及周围液体压力的作用下，其形状不断发生改变，在椭球形和帽形之间不断形变上升。

气泡在不同浓度甲醇水溶液中生成脱离过程，实验结果如图15所示，气速为0.2 m/s。

分析图15(a)、图15(b)可知：气泡与气泡之间很少聚并，气泡的直径符合理论生成的直径；随着甲醇浓度由 1 mol/L[图15(a)、15(b)]增加到 10 mol/L[图15(c)、15(d)]，溶液的表面张力、黏度和密度逐渐变小，气泡生成直径变小，该过程会发生单次聚并的现象。增大气速会出现多次气相聚并，使得气泡脱离直径变大，气泡形状变得不规则。如图15(e)、图15(f)所示，气泡在纯甲醇溶液中表面张力和黏度较小，以气泡链的方式产生，脱离直径缩小，脱离周期变短。在纯甲醇溶液中生成的第一个气泡较大，而后生成的气泡小于第一个气泡，这是因为第一个气泡脱离后气泡尾部压力降低，有利于其后小气泡的形成。高浓度电解液容易造成甲醇的渗透，低浓度电解液又会导致电池功率密度降低，因此选用合适浓度的甲醇溶液是保证电池高功率输出，同时有效克制因高浓度甲醇渗透造成电池自放电的必要手段。模拟工作和实验过程中气泡生长脱离行为具有相同趋势。

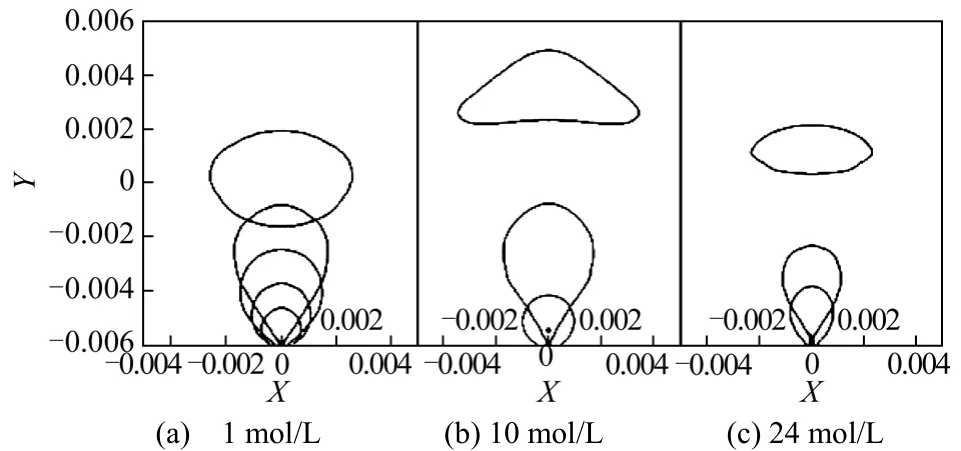
图14 不同甲醇浓度气泡脱离后的形状图

图15 不同甲醇浓度对气泡生长的影响

4 结 论

（1）气泡在扩散层表面生长过程中，由于浮力和表面张力的作用纵向被拉长，同时其尾部受到液体剪切作用不断变细，当浮力大于表面张力时，气泡脱离。

（2）倾斜扩散层表面生成的气泡，其脱离周期较水平扩散层表面短，脱离直径小。

（3）进气速度能改变气泡的生成频率和气泡的生长状态；气速较高时，气泡会发生二次聚并或多次聚并，生成更大直径的气泡。

（4）气泡直径随甲醇浓度的升高而变小，高浓度甲醇溶液中气泡较小，更容易以气泡链的形式生成，有利于气泡脱离。

[1] Baglio V，Stassi A，Matera F V，et al. Investigation of passive DMFC mini - stacks at ambient temperature[J].Electrochemical Acta，2009，54（7）：2004-2009.

[2] 王诚，毛宗强，谢晓峰，等. 小型燃料电池的研究现状与应用前景分析[J]. 化学进展，2006，18（1）：30-35.

[3] Daejin K，Eun A C，Song A H，et al. Recent progress in passive direct methanol fuel cells at KIST[J].Journal of Power Sources，2004，13（1-2）：172-177.

[4] Han J S，Park E S. Direct methanol fuel-cell combined with a small back-up battery[J].Journal of Power Sources，2002，112（2）：477-483.

[5] Yang H，Zhao T S，Ye Q，et al.In situvisualization study of CO2gas bubble behavior in DMFC anode flow fields[J].Journal of Power Sources，2005，139（1-2）：79-90.

[6] Yang H，Zhao T S. Effect of anode flow field design on the performance of liquid feed direct methanol fuel cells[J].Electrochemical ACTA，2005，50（16-17）：3243-3252.

[7] Yang H，Zhao T S，Cheng P. Gas-liquid two-phase flow patterns in a miniature square channel with a gas permeable sidewall[J].International Journal of Heat and Mass Transfer，2004，47（26）：5725-5739.

[8] Delnoij E，Kuipers J A M，Swaaij van W P M. Dynamic simulation of gas-liquid two-phase flow：Effect of column aspect ratio on the flow structure[J].Chemical Engineering Science，1997，52（21）：3759-3772.

[9] Lee Shong-leih，Tien Wen-bin，et al. Growth and detachment of carbon dioxide bubbles on a horizontal porous surface with a uniform mass injection[J].International Journal of Heat and Mass Transfer，2009，52（13-14）：3000-3008.

[10] Xu Xingming，Zhao Guoqun，Li Huiping，et al.Numerical simulation of bubble growth in a limited amount of liquid[J].Engineering Reseach Center for Mold Die Technologies，2010，116（3）：1264-1271.

[11] Gerlach D，Alleborn N，Buwa V，et al. Numerical simulation of periodic bubble formation at a submerged orifice with constant gas flow rate[J].Chemical Engineering Science，2007，62（7）：2109-2125.

[12] 张怀生，王良华，章渊昶，等. CO2气泡脱离扩散层孔口过程的数值模拟[J]. 高校化学工程学报，2010，24（1）：35-40.

[13] 何健烽，章渊昶，姚克俭，等. 直接甲醇燃料电池阳极通道内气泡行[J]. 化工进展，2010，29（5）：831-838.

[14] FLUENT 6.0 Users Guide Documentation[M]. Lebanon，New Hampshire：FLUENT Inc.，2001.

[15] FLUENT 6.3 Users Guide Documentation[M]. Lebanon，New Hampshire：FLUENT Inc.，2006.

[16] Gao H，Ma C F. 2D analytical model of a direct methanol fuel cell[J].Electrochemical Commun，2004，6（3）：306-31.

[17] Bhavaraju S M，Russell T W F，Blanch H W，et al. The design of gas sparged devices for viscous liquid systems[J].AIChE J.，1978，24（3）：454-466.