根的判别式的等价形式及其推论

湖北省赤壁市车站学校 李道生 王荆洲 （邮编：201302）

众所周知，根的判别式是判断一元二次方程有无实数根的重要方法，经过对其结构形式的深入研究与全面分析，我们发现它在解决其他数学问题，特别是不等式问题中有着重要的应用.为此，首先必须换一个角度、换一种形式表述根的判别式，如此才能拓展其应用前景，带给我们耳目一新回味无穷的思维快感.

根的判别式：“若一元二次方程ax2＋bx＋c＝0有实根，则b2－4ac≥0”.

若设方程ax2＋bx＋c＝0的实根为m，则根据根的定义有：am2＋bm＋c＝0，于是，我们得到根的判别式的等价形式：“若am2＋bm＋c＝0（a≠0，m为常数），则b2≥4ac”.

特殊地，取m＝±1，则有推论：“若a±b＋c＝0（a≠0），则b2≥4ac”.

有些竞赛题如果通过如此等价的根的判别式来思考，则可考察我们敏锐的观察能力，培养我们思维的灵巧性，使问题获得简洁巧妙的解法.兹举例如下：

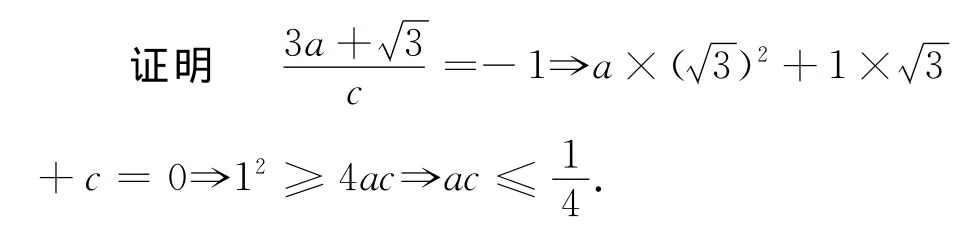
例2 设a、b、c是实数，a＋b＋c＝0，abc＝1，

求证a、b、c中有且只有一个数不小于.

证明 由题设可知，a≠0，b≠0，c≠0，又因为a＋b＋c＝0，abc＝1，所以a、b、c中有且只有一个正数，不妨设b＞0.

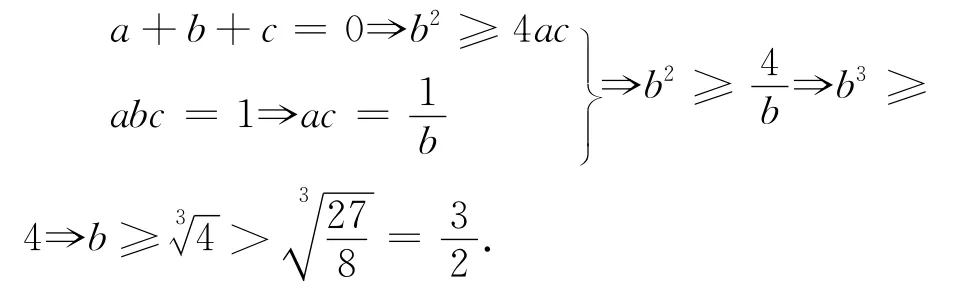
例3 实数x、y、z满足x＝6－y，z2＝xy－9，求证：x＝y.

证明x＝6－y⇒x－6＋y＝0⇒62≥4xy⇒xy≤9，

又z2＝xy－9，⇒z2≤0⇒z＝0，进而易得：x＝y＝3.

用此类似的方法，我们可轻易解决以下难题：

1.“若a、b、c均为实数，且a＋b＋c＝0，abc＝2，那么｜a｜＋｜b｜＋｜c｜的最小值达到________（湖北省黄冈市初中数学竞赛试题）.

2.已知a、b、c均为实数，且a－b＝8，ab＋c2＋16＝0，求证：a＋b＋c＝0.

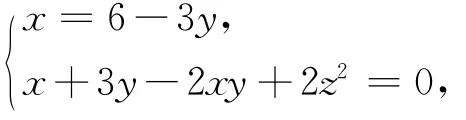
则x2y＋z的值为__________（1998年上海市初中数学竞赛试题）

最后，我们给出有关根的判别式的其它变换形式，供大家学习思考.

命题1 已知am2＋bm＋c＝0（a≠0，m为常数）

（1）若m＝－，则b2＝4ac；

（2）若m≠－，则b2＞4ac.

命题2 已知am2＋bm＋c＝0（a≠0，m为常数）

（1）若b2＝4ac，则m＝－；

（2）若b2＞4ac，则m≠－.

命题3 若am2＋bm＋c＝0（a≠0，m为常数），则存在常n数，使

（1）mn＝，m＋n＝－；

（2）an2＋bn＋c＝0.

根的判别式貌似简单平常，但从求新求变的角度去思考，我们就能从中挖掘出许多令我们意想不到的结果，可谓平凡中隐含着奇特.