一堂没有结尾的复习课

安徽省砀山中学 辛 民 （邮编：235300）

尊重学生的想法，善待学生的思维，正确把握教学契机，并作出积极的反应，是形成高效课堂，提高复习效果的有效策略.

1 问题背景

在进行重要不等式复习时，课前备课组讨论认为不等式知识点多，覆盖面广，思想方法内涵丰富，应用广泛，作为研究数学的重要工具渗透在数学的众多章节，既是中等数学的重要内容，又是学习高等数学的必要基础，也是高考重点考查的内容之一.基于上述认识《重要不等式及应用》教学设计，基本过程是师生先共同回忆梳理阐释常见的基本不等式，精选高考试题说明不等式的简单应用，不料课堂教学刚刚开始即出现了意想不到的结果，是收是放、是羁是疏，两种不同的教育理念的碰撞，肯定是两种不同教学结果.笔者采取了顺应学生贴着学生最近发展区探究前行的教学方法取得了较好的效果，以下展示整个原生态教学过程，与同行共享教育的愉快.

2 教学过程

师：由于不等式：a2＋b2≥2ab（a，b∈R，a＝b时取等号）具有变式多、应用广、内涵丰富，因此称其为重要不等式，今天我们就以它为基础进行展开复习，请举例说明它在数学、生活中的应用：

生1：直角三角形斜边长为定值，等腰三角形的面积最大.

师：如何用数学语言说明！

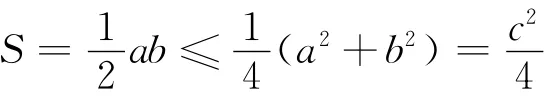
生2：（性格比较内向，与同桌小声交流）直角三角形斜边为定值时等腰三角形面积有最大值，自然会问三角形中一角及对边为定值，面积是否存在最大值？如何求？

（教与学的碰撞，产生思维的火花，稍纵即逝.决定放弃课前的预设，顺应学生，就此问题探究展开教学）

师：很好！学问贵在疑问，有了疑问就能激发思考，请同学们利用已有的知识、展开联想解答生2的问题.

生3：既然直角三角形推广为一般三角形，直角三角形中问题用勾股定理解决，一般三角形可考虑余弦定理，按这一思路我有如下解法：

已知，在ΔABC中，AB＝c，c＞0，∠ACB＝θ，θ∈ （0，π），求ΔABC面积的最大值.

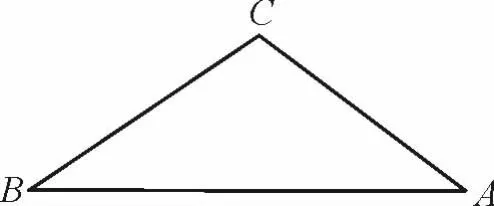
解 如图，设BC＝a，AC＝b，由余弦定理得：

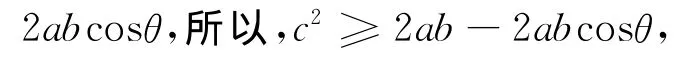
所以当ΔABC为等腰三角形时面积最大.

师：利用类比我们既可以发现问题、也可以解决问题，希望同学们在今后的学习中多思、多想、多问，谁还有想法？

生4：利用正弦定理我不能进行到底，但我想此法应该行！

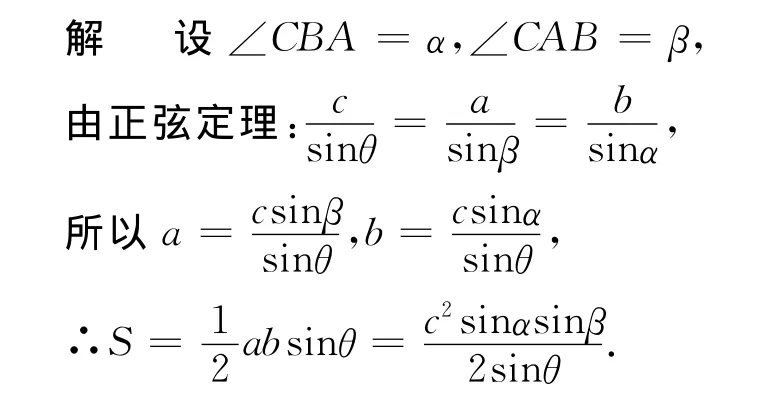
至此以下我没有办法完成.

师：解决问题遇到障碍时，重新审视题目挖掘题设条件，矫正解题思路是扫除障碍顺利解答的有效策略，请思考题目中还有没有条件没有用？如何用？

生4：题目中定值角度还没有利用，即α＋β＝π－θ，

师：如何将α、β与α＋β联系起来？

生5：（脸上露出微笑）可以！

cos（α－β）－cos（α＋β）＝ 2sinαsinβ得2sinαsinβ≤1＋cosθ（α＝β时取等号）

师：解题遇到困难时，再次审视题目条件、结论，充分利用条件可以为彻底解决问题增加正能量.

生6：受此启发，我利用射影定理得到过程：

解 设CA＝a，CB＝b，∠CBA＝α，∠CAB＝β由射影定理得：

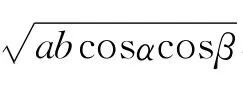
由于cos（α＋β）＋cos（α－β）＝2cosαcosβ

所以2cosαcosβ≤1－cosθ，不等号方向相反，无法进行下去.

师：题目理解无误，公式、知识运用正确，结果出现矛盾，就需要我们重新梳理解题思路，检查解题的每一步是否合理是否正确.

事实上，第一次利用重要不等式的条件不具备.但是我们有理由相信既然用正、余弦定理能解决，用射影定理就一定能解决，关键是如何正确的利用射影定理及不等式放缩？

生7：生6解答利用不等式时不能保证acosα、bcosβ为正值、相等，故运用不等式错误，可作如下变形：

师：充分挖掘题目的隐含条件，保证定理、定义的运用的条件满足，是正确解题的前提.

生8：要求三角形面积的最大值，底边为定值，只要求点A到直线BC的距离最大值，可得到如下解法：

解 设∠CBA＝α，∠CAB＝β，点A到BC的距离为d，则c＝d（cotα＋cotβ）

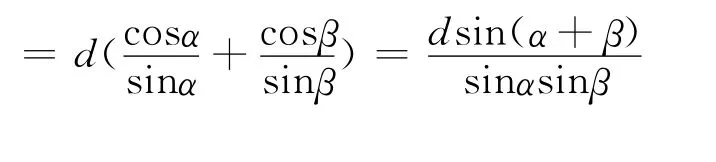
师：很好，由三角形面积等于底乘高，底边长为定值，因此只需求高的最大值即可，由此可以看出从原始定义出发是解决问题的有效方法.

生9：由题设条件可知，三角形的顶点C可以认为是在以AB为弦圆弧上运动的点，显然点C在圆弧的中点时，三角形的面积最大，此时三角形为等腰三角形.

师：解法简洁、自然，从问题的本质出发是优化解题过程的有效策略.

生10：利用向量运算我得到了如下解法：

师：多角度、多层面认识问题，是深化问题的理解，优化解题过程提高解题能力的重要环节，谁还有什么想法？

生11：刚才的问题可以认为是对线段的张角为定值，构成三角形面积的最值问题，变换题目条件得到下面问题：

已知：在ΔABC中，AB＝a（a＞0），CB＋CA＝l（l＞0），求ΔABC面积的最大值.

众生：显然，点C的运动轨迹是椭圆，当点C位于椭圆短轴端点时面积最大.

师：问题精彩，解答漂亮，充分显示了我们的聪明智慧.

生12：老师我也有一个问题：

已知AB＝c，以线段AB为弦弧长为l，求弓形的面积的最大值.

生13：

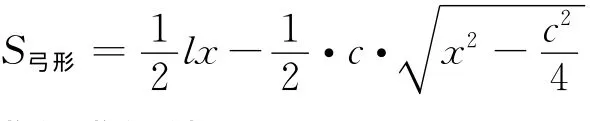
师：质疑是自主学习重要形式，是修正错误、完善认识重要途径，主动思考是质疑的前提，完善认识提高能力是长期质疑的必然结果.一个问题两种解答，孰对孰错，请同学们认真思考！

生15：弧长、弦长都确定时，所在的圆的半径是唯一确定的值，因此弓形唯一.

事实上：当弓形所在的扇形弧长小于半圆时，设圆的半径为r，则圆心角的弧度数为，在ΔOBA中，，即，显然，由数形结合知：有唯一解.

当弓形的弧长大于半圆时，同样可以说明.

师：合作、交流，是深化理解形成正确认识、提高能力重要途径.

生16：老师：我也有一个问题，

已知：四边形ABCD一边AB＝c（c＞0），其他三边长的和为l，求四边形ABCD面积的最大值.

我不能利用已知条件表示四边形的面积，是否可增加一个条件，使得四边形的面积容易表示.

生17：增加一个条件，将四边形特殊化，如四边形ABCD是以AB为底边的等腰梯形就可以啦.

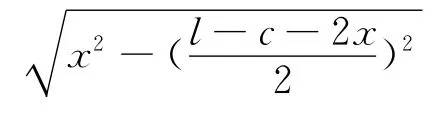
解 如图，设等腰梯形的腰长为x，则高可表示为

叮—叮—叮—下课铃响起了.

思绪不得不停，经梳理布置如下作业：

课后请同学们完成下面的问题，有兴趣的同学请继续思考，一般四边形面积的表达式；

阅读数学（选修2－1）中类比推理；

几何证明选讲（选修4－1）中的阅读材料：定长闭曲线最大面积问题.

3 几点感悟

（1）真正有效的课堂，不是教师用多快的速度把一个完整的知识体系呈现给学生，而是通过基本的数学活动丰富学生的思维方法、理解基本原理和核心概念，在学生的需要处自然地设置学生要学的问题，捕捉偶发的教育契机与智慧的火花，并做积极地回应，在教学的开始为了解学生对定理的理解程度，设计“试举例说明重要不等式在数学生活中应用”的问题，思维起点低，方向明确，顺应学生思维的形成与发展规律，引起了学生的思维共鸣使学生产生问题意识，激发学生认识的冲动性和思维的活跃性，有利于学生从本质和源头上理解知识，让探究的思路自然、流畅.

（2）高三复习不同于新课学习、章节的复习，是学生站在高中数学整体高度上“二次学习”，学生已具备了较丰富的知识，初步具有了一定数学思考能力，这为教师引导学生探究问题提供了有利条件.但是如何让学生自然地投入到自主学习之中，不断地在愉悦的学习过程中体验成功的乐趣，从而使学习变得轻松自在，显然教师的适时引导、指导是十分必要的，笔者认为，在起始阶段设置恰当问题，引入话题，在思维受阻适时疏导（如生4、7等），在关键处给予引导，在方法技能上实行指导，不断的引发学生思考，让学生的思维自然而然地投入到探究学习之中.

（3）数学教学的最终目的，并不是让学生记住多少知识，而重要的是能够使他们自然领悟到学习数学的思想方法及人生哲理.本节课学习过程以学生为中心、以问题为线索，始终以“发现、解决、再发现、再解决”牵动学生的思维，使他们亲身经历了问题的探究过程，深刻领悟科学的研究方法，使学生在理解、掌握知识的同时，开放知识、质疑知识、批判知识、探究知识、反思知识、创新知识，从而获得智慧的力量，感受到了知识发展的迂回曲折，有利于求实、说理、批判、质疑等理性思维的培养，进一步激发学生学习数学的热情.

本节课虽没有按照课前的预设完成教学任务，但是在学生思维的深处留下的痕迹是课前无法预知的，正如章建跃博士说，课堂教学中，如果我们的教学不能打动学生，学生对我们的教学无动于衷，那么他们就不可能心领神会的心灵共鸣，我们讲得再精彩也只能无功而返.