发挥“所求”在解题中的作用

安徽省淮北市实验高中 纪迎春 （邮编：235000）

解数学题一般的思路都是从题中所给的已知条件出发，利用所学知识，通过推导，直接得出正确结论——题目的所求或所证，即从已知到所求.但有时由于题中已知条件过于抽象、复杂，往往使解题者有无从下手的感觉，影响问题的解决，如果这时能关注一下题中的“所求”，从中发现其隐含的重要信息，则可使解题者有“众里寻她千百度，蓦然回首，那人却在灯火阑珊处”的美妙感觉.这里仅就2013年3月7日安徽省江南十校高三联考数学试卷中的几个问题谈一些不成熟的感受.

例1 （理科第15题）已知△ABC的内角A、B、C成等差数列，且A、B、C所对的边分别为a、b、c，则下列命题中正确的有__________（把所有正确的命题序号都填上）.

①B＝；

②若a、b、c成等比数列，则△ABC为等边三角形；

③若a＝2c，则△ABC为锐角三角形；

⑤若tanA＋tanC＋＞0，则△ABC为钝角三角形.

例2 （文科第10题）对于集合｛a1，a2，…，an｝和常数a0，定义：

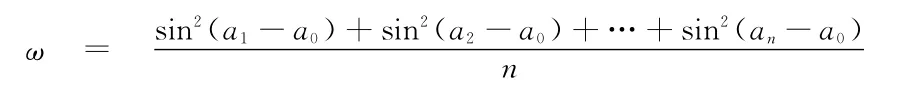
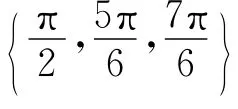
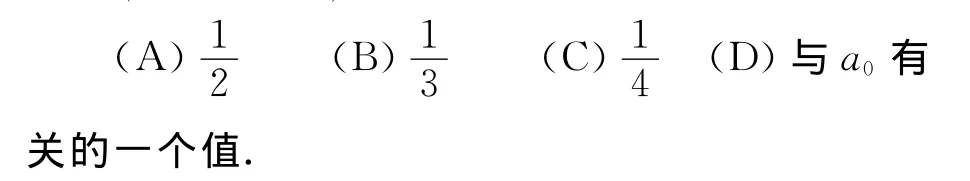
本题同样也是文科生错误率较高的一道题，原因是学生对

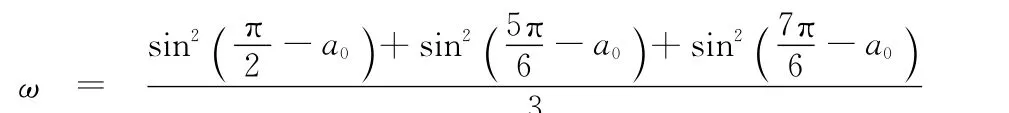
的化简有畏惧感，同时也会因为化简时公式的运用不当或计算有误，而得不出正确的结论，但如果注意观察题中的所求，即所要选择的四个选项，会发现其实不是四选一，而是二选一，ω要么是定值，要么是与a0有关的一个值，到底是哪一个结果，只要让a0取两个不同的特殊值检验，若为同一值，就选这个值对应的选项，若不为同一值，则选（D）.此时学生只要取a0＝0和a0＝π，就很快可以计算出ω的值均为，问题也就很快得到解决.

例3 （理科第18题）如图1，直角梯形ABCD中，∠A＝ ∠B＝90°，AD＝AB＝2，BC＝3，E、F分别是AD、BC上的两点，且AE＝BF＝1，G为AB中点，将四边形ABFE沿EF折起到（如图2）所示的位置，使得EG⊥GC，连接AD、BC、AC得（图2）所示六面体.

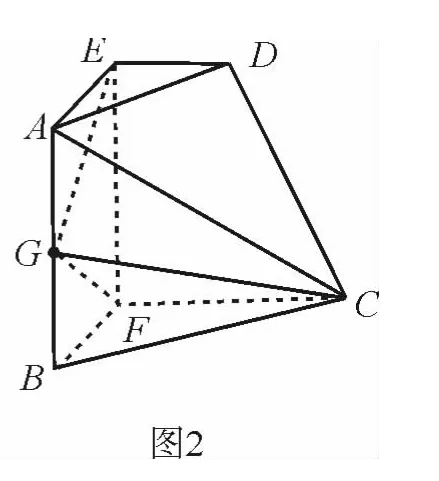
（Ⅰ）求证：EG⊥ 平面CFG；

（Ⅱ）求二面角A－CD－E的余弦值.

学生解答本题第（Ⅰ）问基本没问题，但在做（Ⅱ）时，有很多同学直接就下图建坐标系F－xyz.而忽略了FB，FC，FE两两垂直的证明而丢了分，也有个别学生没看出FB，FC，FE两两垂直而没建系.实际上只要关注了第（Ⅰ）问的结论EG⊥平面CFG，就很容易推导出FC⊥BF，继而得出FB，FC，FE两 两垂直.

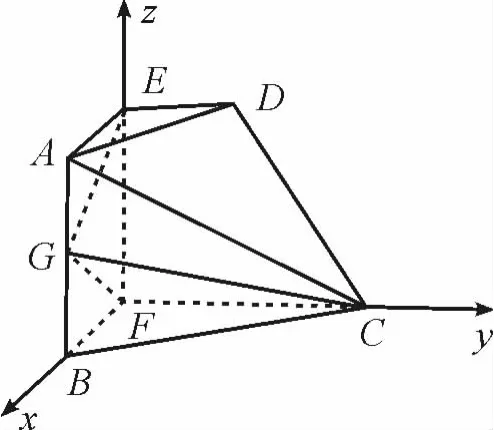
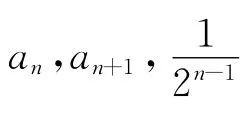
（Ⅰ）求证：｛2n－1an｝为等差数列，并求出数列｛an｝的通项；

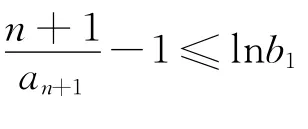
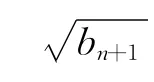
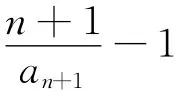
观察要证不等式，可发现：① 左边是数列｛lnbn｝的前n项和；②右边是等比数列的和，甚至有的同学会发现右边是等比数列｛2n－1｝的前n项和；③左边≥右边.这时就比较容易想到要在等式bn＋1＝bn·（bn＋1）同取自然对数，得lnbn＋1＝lnbn＋ln（bn＋1），继而得lnbn＋1＞2lnbn.或由等式bn＋1＝bn·（bn＋1）知，bn＋1＞，两边同取自然对数 得lnbn＋1＞2lnbn.故lnbn＞2lnbn－1＞22lnbn－2＞ … ＞2n－1lnb1＝2n－1，n≥2.n＝1时，lnb1＝lne＝1.

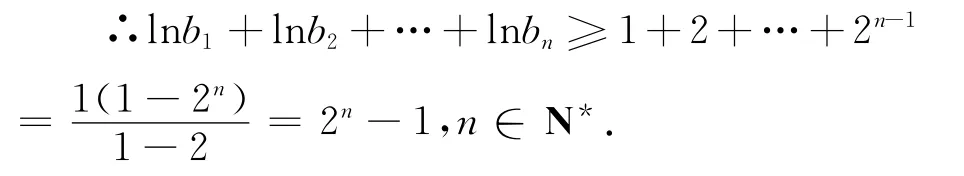
本题也有学生想到用数学归纳法证明，但最终仍会归结为证明lnbn≥2n－1，n∈N＊.

总之，要想快速准确地完成解题，不仅要有基本的数学知识和解题能力，还要学会从“所求”中挖掘有用信息，才能在茫茫求解线索中，寻找到快速正确的道路，达到“柳暗花明又一村”的收获.以上只是在评阅江南十校高三联考数学试卷时一些粗浅的认识，不到之处敬请批评指正.