感悟问题解决，积累活动经验

浙江省宁波市镇海区澥浦中学 刘 勇 （邮编315204）

从某种意义上讲，教学的最终目的是要使学生能自主地解决各种问题.问题解决的过程是如何展开的？怎样才能培养学生问题解决的能力？这历来是教育学家和心理学家探讨的重点.美国著名的哲学家，教育学家杜威早在1910年就提出了“问题解决五步法”的理论，其中第一步就是“感觉到问题的存在”.因此新课程标准强调数学课堂教学中应注重学生的数学体验，在课堂上积累基本的数学活动经验，把数学教学与学生的生活体验相联系，把数学问题与生活情境相结合，培养学生认真观察、自主探究的能力和把实际问题转化为数学问题的能力.

下面，谈一谈本人在把生活中的一些问题引入到课堂教学中的一点体会：

1 用生活实例创设问题情境，激发学生的学习情趣

《数学课程标准》在学段建议中指出：“数学教学要密切联系学生的生活实际，从学生的生活经验和已有的知识出发，创设生动有趣的情境.”因此，在数学课堂教学中，教师可根据学生的年龄特点和生活体验，科学、有效地创设与学生的生活实际相联系的生活情境，让学生在熟悉的生活情景中愉快地探究数学问题，体会自身生活环境中存在的数学现象，体验学习数学的乐趣，激发学生学习数学的情趣，使学生能积极主动地去探索并解决数学问题.

例1 教学“直线、射线、线段”（1）时，先创设如下生活情境：

班委会为了解决同学们下雨天雨具的存放问题，决定在教室外墙钉一根带有挂钩的木条，班主任请班长带上钉子把木条固定好.请问班长至少需带几颗钉子？请大家试一试.

（学生用纸条替代木条，用硬纸板替代墙壁，用图钉替代钉子分组实验.）

学生通过实验得出结论：用一颗钉子钉木条时，木条是松动的，用两颗钉子钉木条时，木条就能固定了.

再进一步引导学生动手操作完成下列问题：

（1）过一点O画直线，可以画几条？

（2）过两点A、B画直线，可以画几条？

学生通过动手实践、观察分析，得出结论：

（1）过一点可以画无数条直线.

（2）过两点可以画一条直线、并且只能画一条直线.

从而得到直线的性质：两点确定一条直线.

这样创设问题情境，体现了数学知识与生活实际的紧密联系，让学生在熟悉的生活环境中愉快地学习，轻松地获得数学知识.不仅能使学生加深对直线性质的理解，又能使学生感受到数学就在我们身边，激发学生学习数学的兴趣.

例2 教学“探索确定位置的方法”

为了激发学生的学习热情，在课前引入中设计了“鲁滨逊漂流记”的片断，当鲁滨逊在荒岛上睁开眼睛的一瞬间，他想到的是什么？他说的第一句话是什么？让学生进入到这种情景，设身处地的思考这个问题，就会引出“我在哪里？”的疑问，从而过渡到“怎样确定位置”这一课题.

因为学生进入了情景中，就有了某种需要，有需要就会主动要求，主动探索，而这种要求和探索正是老师们所迫切希望学生展现出来的，所以贴近学生生活的实例，能引起学生共鸣的情景不妨多关注，多收集.

2 讨论生活中的数学，培养学生的“数学建模”能力

生活中的数学无处不在，不同的实际问题往往具有相同的“数学模型”；同时，相同的实际问题又可以构建不同的“数学模型”.培养学生从实际问题中抽象出代数模型，用数学知识解决生活中的实际问题，新的教材内容更能体现这一点.在数学课堂教学中，教师要充分利用生活中的数学知识，把书本上的知识放在生活中来学习，放手让学生去讨论、去探索，通过学生的合作交流来设计最佳方案，培养学生灵活机动地用数学知识解决生活问题的能力，使生活问题数学化.

例3 如图：要设计一本书的封面，封面长27cm，宽21cm，正中央是一个与整个封面长宽比例相同的矩形，如果要使四周的彩色边衬所占的面积是封面面积的四分之一，上、下边衬等宽，左、右边衬等宽，应如何设计四周边衬的宽？

教学时，教师先提出问题让学生讨论：

（1）书的封面长与宽之比是多少？ （27∶21＝9∶7）

（2）中央矩形长与宽之比是多少？ （9∶7）

（3）上下边衬与左右边衬的宽度之比是多少？（9∶7）

（4）设上下边衬的宽度均为9xcm，那么左右边衬的宽度是多少？ （7x）

（5）中央矩形的长宽分别是多少？

（长（27－2×9x）cm，宽（21－2×7x）cm）

（6）要使四周彩色边衬的面积是封面面积的四分之一，则中间矩形的面积占封面面积的几分之几？（）

再进一步提出问题：

如果换一种设未知数的方法，是否可以更简单的解决上面的问题？请大家试试看.

学生通过讨论交流，得出结论：设中间矩形的长为xcm，则宽为xcm，

解方程求出中央矩形的长和宽，从而求出四周边衬的宽度.

最后提出思考：如果我们把原来的图形通过平移，变成如图的情形，又可以列出怎样的方程？

这样让学生通过在现实且富有挑战性的实际问题中，多角度分析问题、认识问题，多策略思考问题、讨论问题，尝试解答问题的方法，有利于培养学生的“数学建模”能力和探索精神.

3 结合生活经验，引导学生主动探索新知

在数学课堂教学中，教师要把数学知识的学习与学生的生活经验有机的结合起来.有些数学的知识点，可以通过学生的交流讨论、动手操作等合作活动，让学生真正感受到数学知识就在我们的日常生活中，用自身的生活经验获得探索数学知识的方法，提高用生活经验解决数学问题的能力.

例4 教学线段的比较和性质时，先让学生思考下列问题：怎样比较两位同学的身高？并说说你的做法.

这时学生七嘴八舌，各抒己见：

学生甲：让两人背靠背站在一起，再看两人的头顶.

学生乙（补充）：两人应站在同样高的地面上.

学生丙：可以分别测量他们的身高.

然后教师在黑板上画两条任意长的线段AB、CD，让学生想一想，并讨论交流：同学们已经会比较两个同学的身高了，那么怎样比较两条线段的长短？

学生通过讨论交流，结合比较两位同学身高的经验，得出结论：放在同一条直线上比较；

如图：

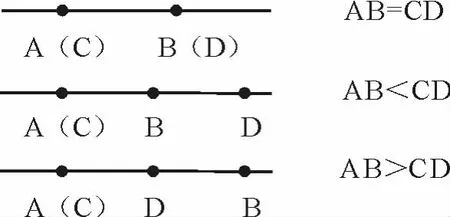
用度量的方法比较；

如果AB＝12cm，CD＝20cm，EF＝12cm，则AB＝EF，AB＜CD，CD＞EF.

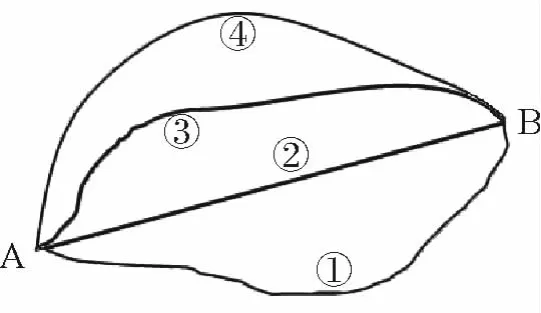
（2）如图：从住宅区A到学校B有四条道路，如果让你选择，你会走哪一条路，说出你的理由？

学生根据自身的生活经验，不难得出：选择道路②路程最短.从而得出结论：两点之间，线段最短.

这样，通过生活经验的启发，和想一想、做一做、讨论交流等方式，把抽象的数学内容转化为学生身边熟悉的生活现象，既使学生获得了新知识，又培养了学生自主学习的习惯，发展他们用生活经验获取知识、解决问题的能力.

4 运用数学知识，解决生活中的数学问题

学习的目的在于应用，数学教学要关注与学生日常生活息息相关的生活问题，让课堂教学与生活数学紧密结合起来，提高学生用数学知识解决生活中的数学问题的能力，让生活问题“数学化”.

例5 教学“立体图形的平面展开图”时，先指导学生以小组合作的形式，把课前准备好的长方体、正方体、圆柱体模型用剪刀展开，观察它们的平面展开图，从而得出：不同的几何体的平面展开图有所不同.再让学生用学过的长方体、正方体、圆柱体的平面展开图的知识、美术知识设计制作长方体、正方体、圆柱体形状的包装盒，以此激发学生的学习兴趣.

例6 建筑工人在砌墙时通常用一根细线来测量墙面是否平直，你能解释一下其中蕴含的数学知识吗？

例7 公路上的测速仪用来测量汽车行驶时是否超速，测速仪本身有一个视野的限制，但是能测出汽车通过整个视野的时间，你能根据这个数据判断汽车是否超速吗？如何通过数学计算解释这个原理.

反思分析 新课程标准下的数学教科书更重视将教科内容和实际生活紧密联系起来，在章节前都配有情景问题和插图，一方面增强趣味性，另一方面体现数学源于生活，用于生活.在课堂教学中引导学生学会观察生活，善于从生活实例中捕捉数学问题，使学生充分认识数学来源于生活，又是解决生活问题的基本工具，提高学生学习数学的兴趣.只要我们善于捕捉生活，将生活中有趣的数学问题融人到课堂教学中，数学就不再是一门枯燥无味的学科，数学课堂氛围也会活跃无比.