对一道高中数学教师综合素质大赛题的思考——兼谈编制数学题的方法
安徽省合肥市第六中学 侯曙明 苗大文 (邮编:230001)
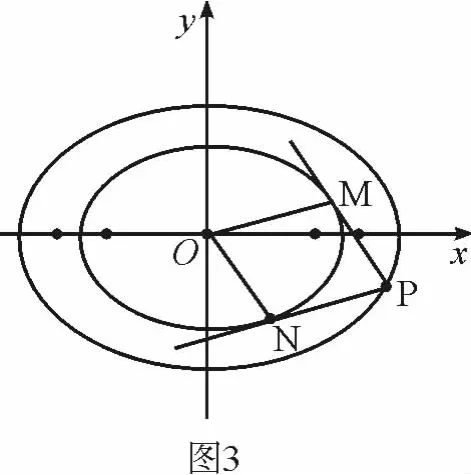
合肥市第二届高中数学教师综合素质大赛暨第十届高中数学优秀课比赛(预赛)日前落幕,比赛内容为“六个一”(解一道题,命一道题,说一节课,评一节课,上一节课,谈一体会),其中,在“命一道题”环节中,给出了下列问题:

试问ΔMON的面积SΔMON是否为定值?
在题设条件下,再编制若干个正确的新命题.
(每个正确的新命题给10分)
赛后发现,在命题环节中,参赛教师普遍表现不太理想,反映出教师编制命题的能力欠缺,对问题的背景认识不足,命题的视野不宽,方法单调.本文首先针对上述命题,编制一系列新命题,然后谈一点编制命题的方法和策略.
1 命题编制
首先,容易证明如下的
引理 设M(acosα,bsinα),N(acosβ,bsinβ),kOM,kON都存在,则下列关系成立:
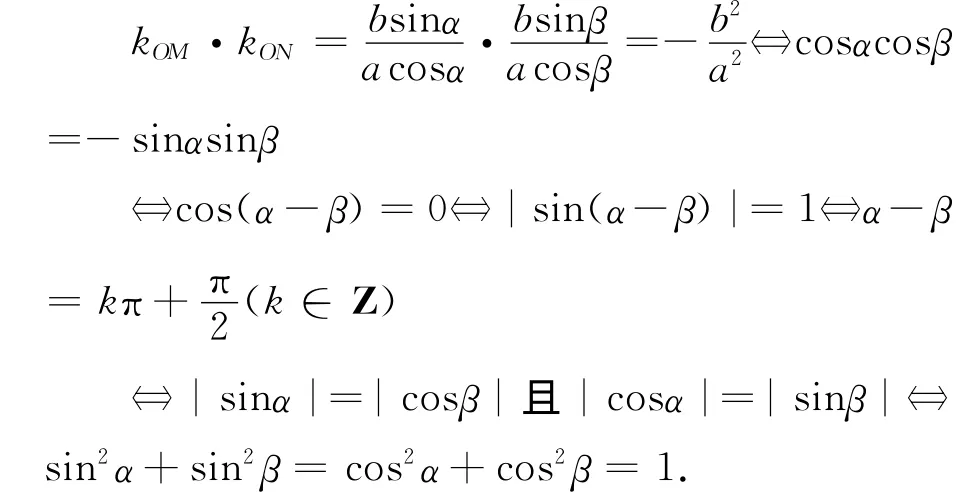
由上述引理,可以得到
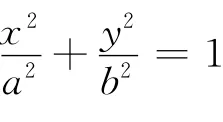
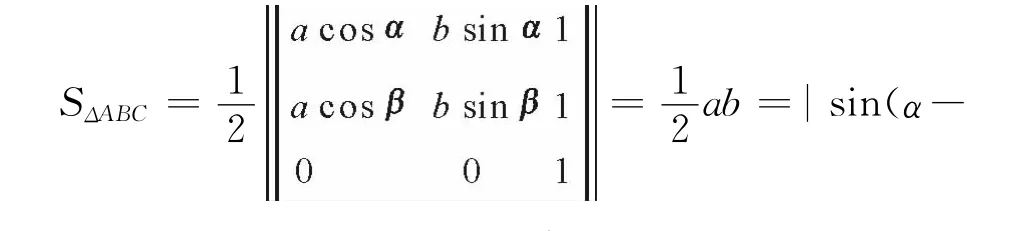
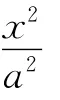
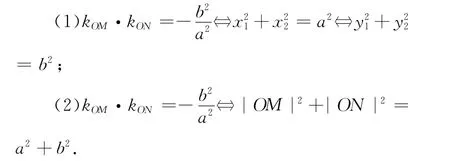
证明 设M(acosα,bsinα),N(acosβ,bsinβ),则
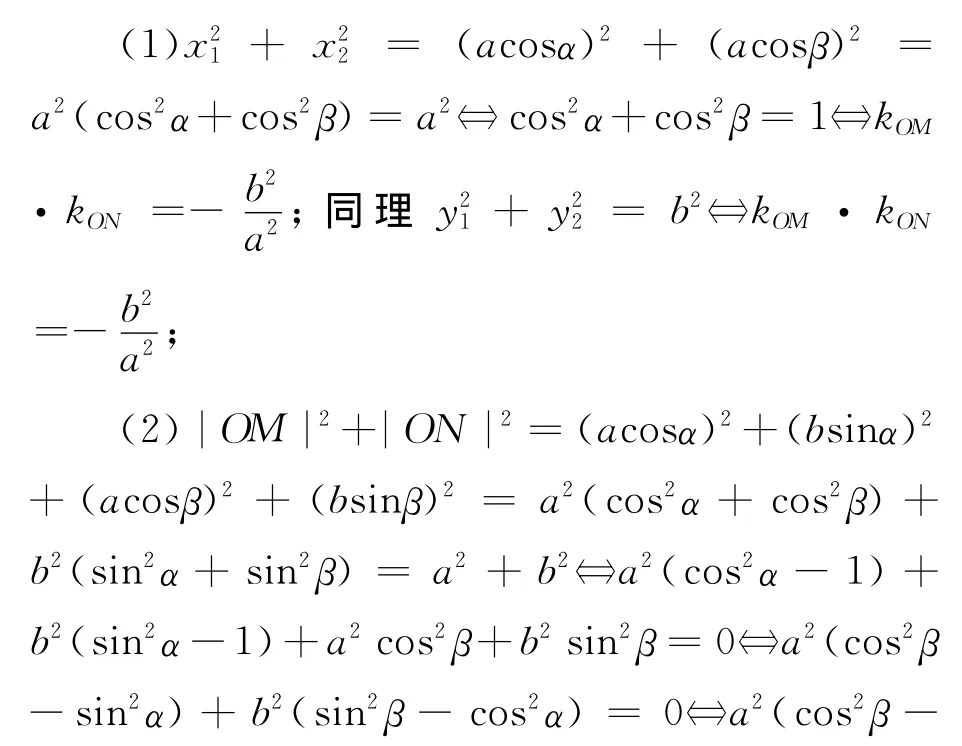


证 明 |MN|2= (acosα-acosβ)2+(bsinα-bsinβ)2=a2(cos2α+cos2β-2cosαcosβ)+b2(sin2α+ sin2β- 2sinαsinβ) =a2(1 -2cosαcosβ)+b2(1 -2sinαsinβ)=a2+b2-2(a2cosαcosβ+b2sinαsinβ)=a2+b2+2(a2-b2)sinαsinβ,所以|MN|2-(a2+b2)|=2(a2-b2)|sinα||sinβ|=(a2-b2)·2|sinα||cosα|=(a2-b2)|sin2α|≤a2-b2,

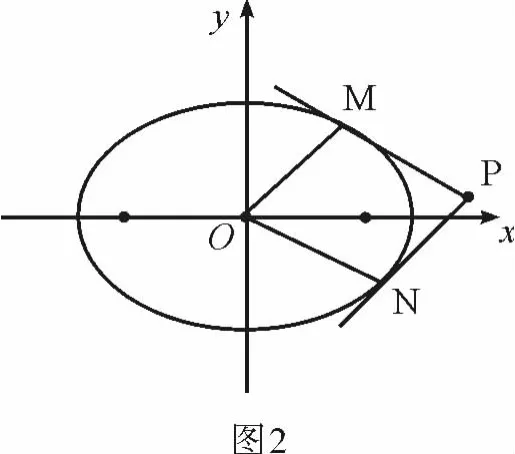

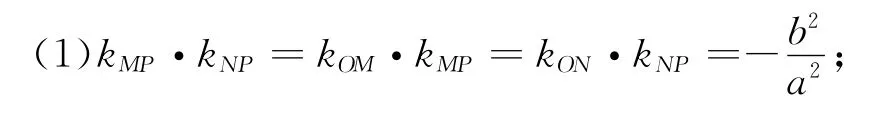
(2)四边形OMPN是平行四边形.
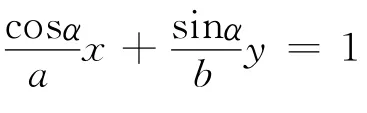
(2)由(1)易知,四边形OMPN显然是平行四边形.

证明 设M(acosα,bsinα),N(acosβ,bsinβ),
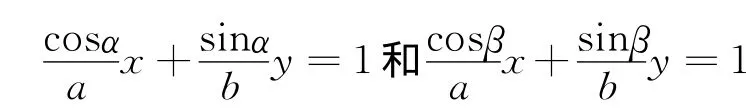
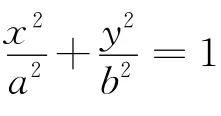
根据椭圆的对称性结合命题4和命题5,下列两个命题是正确的.
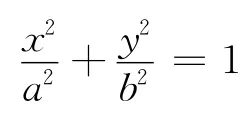
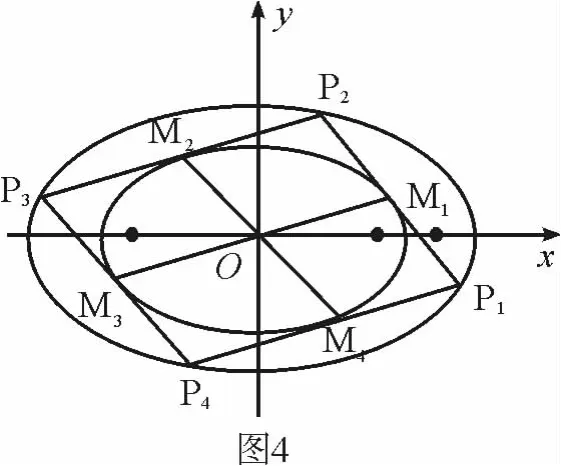
2 一点思考
中学一线教师经常出卷,从单元测验到期中、期末考试卷,还有高考模拟卷.通常是组题为主,很少创编新题.创编新题的确有难度,相信各位老师都有切身感受,这是一个值得好好研究的课题.下面结合命题实践,谈谈编制命题的一些体会.
(1)通过类比编制命题.类比是以比较为基础,通过比较,找出两个不同对象的某些属性的相似点或近似程度的思维方法.利用类比的这一特性,通过类比和比较,我们可以在一些相近的知识点上创编出新题来.如2003年北京卷第18题就是由圆中的“蝴碟定理”,考虑到圆所具有的对称性,将圆换成椭圆或其他对称图形,“蝴碟定理”是否仍然成立?于是就有了那道经典题,一时传为美谈.高考中的这类创编题不胜枚举.
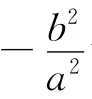
(3)通过特殊与一般的关系编制命题.从特殊到一般,再由一般到特殊是人们认识客观世界的基本过程之一.近年来高考命题特别是自主命题以来,一些植根于高等数学的试题,取其特殊化的情况,也是命题专家常用的手法.如1996年全国卷第25题是函数与不等式的结合题,是马尔科夫定理的一个特例;1999年全国卷第10题和2005年全国卷Ⅰ第5题,两道立体几何选择题都是牛顿—辛普生公式的特例;2012年安徽卷理科第21题的背景是计算方法中的不动点理论,此所谓“高观点、低切入”.现在的中学教师都受过良好的高等教育,很多都具有研究生学历,高观点下的创编新题应该是有基础的.
(4)通过变更命题条件和结论、推广命题编制命题.命题由条件和结论构成,将条件和结论进行适当的组合可构成新命题,其中,构造逆命题是最常用的手段;推广命题更是涵盖了原命题,结论更加深入,也是编制命题常用手段.本文中的命题7实际上是命题6的逆命题,沿着上面探讨的递进过程看它不是一个难题,但如果作为一个独立命题就有一定的难度.该命题条件简洁,结论优美,是一道不错的命题.
笔者参与过各类考试试卷的命制,我们以为课本中的例、习题、高考题、竞赛题是我们“取之不尽、用之不竭”的素材,这些命题是教材编写专家和命题专家深思熟虑的结果,值得我们去学习、思考和研究.通过对这些问题的进一步开发,可以编制出有针对性的、新颖别致的新命题,供教学使用.对教师而言,编制命题的过程体现了研究性学习的过程,是知识体系由封闭到开放的过程,也是提高命题能力的过程,是促进教师专业化发展的一个渠道,是优秀教师的成长之路.

