直线与抛物线位置关系的另类判别方法

安徽省阜阳市红旗中学 张 震 吴冬梅 （邮编：236112）

文［1］、文［2］分别研究了直线与椭圆、双曲线位置关系的不同判别方法，本文将给出有关直线与抛物线位置关系的另类判别方法.

结论1 直线l：Ax＋By＋C＝0（ABC≠0）抛物线y2＝2px（p≠0）

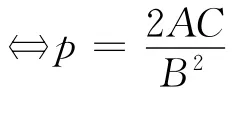
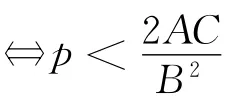
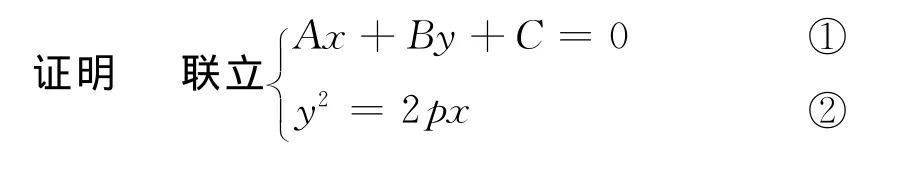
Ay2＋2pBy＋2pC＝0，

△ ＝（2pB）2－4A·2pC＝4p（pB2－2AC），

结论2 直线l：Ax＋By＋C＝0（ABC≠0），

抛物线x2＝2py（p≠0），

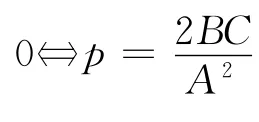
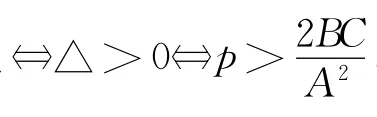
探究结论1和结论2 推广至一般情况，可得下面结论：

结论3 直线l：Ax＋By＋C＝0（ABC≠0），

（2）直线l与抛物线相交 ⇔（y1＋y2）（y1－y2）＞－p2；

（3）直线l与抛物线相离 ⇔（y1＋y2）（y1－y2）＜－p2.

最后联立直线l与抛物线：

⑤ 代入 ① 式（y1＋y2）（y1－y2）＝－p2，

于是 （1）直线l与抛物线相切 ⇔△ ＝0⇔（y1＋y2）（y1－y2）＝－p2；

（2）直线l与抛物线相交 ⇔△ ＞0⇔（y1＋y2）（y1－y2）＞－p2；

（3）直线l与抛物线相离 ⇔△ ＜0⇔（y1＋y2）（y1－y2）＜－p2.

结论4 直线l：Ax＋By＋C＝0（ABC≠0），

（2）直线l与抛物线相交 ⇔（x1＋x2）（x1－x2）＞－p2；

（3）直线l与抛物线相离 ⇔（x1＋x2）（x1－x2）＜－p2.

联立直线l与抛物线：

⑤ 代入 ①（x1＋x2）（x1－x2）＝－p2

于是 （1）直线l与抛物线相切 ⇔△ ＝0⇔（x1＋x2）（x1－x2）＝－p2；

（2）直线l与抛物线相交 ⇔△ ＞0⇔（x1＋x2）（x1－x2）＞－p2；

（3）直线l与抛物线相离 ⇔△ ≤0⇔（x1＋x2）（x1－x2）＜－p2.

应用举例

例 当m为何值时，直线l：y＝2x＋m2＋1与抛物线y2＝16x相切、相交、相离.

解法一y＝2x＋m2＋1即2x－y＋m2＋1＝0.这里A＝2，B＝－1，C＝m2＋1.

在抛物线y2＝4x中，p＝8，

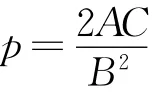
解法二y2＝16x，准线l1：x＝－4，直线l2：x＝4，

解得y1＝m2－7及y2＝m2＋9，

所以y1＋y2＝2m2＋2，y1－y2＝－16，

（y1＋y2）（y1－y2）＝－32（m2＋1）.

由结论3：（y1＋y2）（y1－y2）＝－p2，

即－32（m2＋1）＝－64，m2＋1＝2，m＝±1.

当m＝±1时，（y1＋y2）（y1－y2）＝－p2，直线与抛物线相切.

当－1＜m＜1时，（y1＋y2）（y1－y2）＞－p2，直线与抛物线相交.

当m＝＜－1或m＞1时，（y1＋y2）（y1－y2）＜－p2，直线与抛物线相离.

1 晏银林.直线与椭圆的位置关系的另类判别方法［J］.数学教学，2010（5）：32—33

2 姜坤崇.直线与椭圆、双曲线的位置关系的又一判别方法［J］.数学教学，2011（1）：36