椭圆中两类张角最大值的简证、拓广及其它

安徽省合肥市第一中学 刘 斌 （邮编：230601）

文［1］推证了椭圆中两类张角的最大值，文中得到的两个定理结论优美、用途广泛，是日常教学中必向学生介绍的内容，但该文篇幅冗长、过程繁复.新课标实施后，教学容量较之前大大增加，如何在教学中简洁地证明这两个结论，便成为摆在一线教师面前的一个现实问题.本文首先给出这两类张角最大值的简洁证明，然后证得定理1的类比及其推广.文末给出了可以继续研究的问题.

1 两个定理的简证

定理1 椭圆上一点到该椭圆长轴两端的张角中，以短轴端点到长轴两端的张角最大.

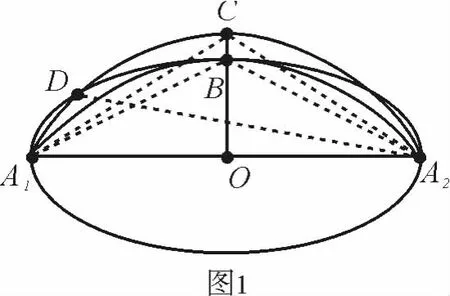
证明 如图1，以椭圆长轴A1A2为弦作弧A1BA2切椭圆于短轴端点B，再以A1A2为弦在其同侧作圆弧A1DCA2与椭圆相交，记其中一个交点为D，射线OB交该弧于点C，则∠A1DA2＝∠A1CA2＜ ∠A1BA2.

定理2 椭圆上一点到该椭圆两焦点的张角中，以短轴端点到两焦点的张角最大.

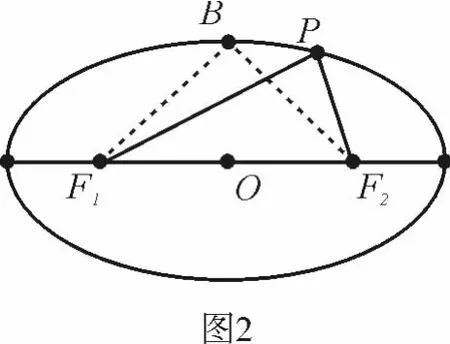
证明 如下图2，记∠F1PF2＝q，椭圆的短半轴长｜OB｜＝b，用第一定义结合余弦定理，易知焦点三角形PF1F2的面积S＝b2tan.注意到当且仅当点P与短轴端点B重合时，面积S取到最大值，即tan此时最大，又∈ （0，），故 此时最大，即∠F1PF2＝q＝∠F1BF2时取到最大值.

2 定理1的类比及推广

定理3 椭圆上一点到该椭圆短轴两端的张角中，以长轴端点到短轴两端的张角最小.

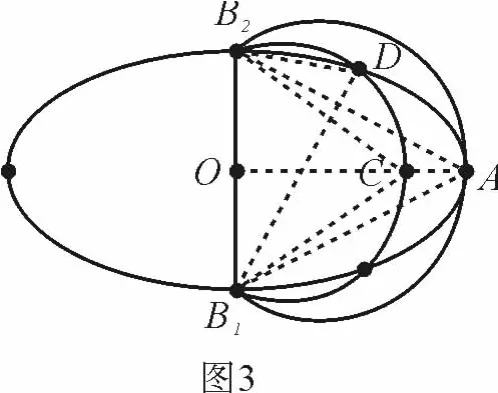
证明 如图3，以椭圆短轴B1B2为弦作弧B1AB2切椭圆于长轴端点A，再以B1B2为弦在其同侧作圆弧B1CDB2与椭圆相交，记其中一个交点为D，线段OA交该弧于点C，则 ∠B1DB2＝ ∠B1CB2＞ ∠B1AB2.

事实上，用同样的方法，可以将定理3进一步推广为定理4，如图4，点G1、G2是椭圆短轴延长线上关于中心O对称的两点.椭圆上一点到G1、G2两点的张角中，以长轴端点到G1、G2的张角最小.

3 深入研讨

由于椭圆短轴上没有所谓焦点，因此，定理2的类比似乎无法探讨.但我们换个角度，自然想到的一个问题是，将定理4中两点的位置由短轴延长线上移动到短轴上来，能否得到类似结论？按此思路，经深入研究，笔者利用坐标法综合到角公式、均值不等式和函数最值，得到了如下结论.

定理5 如图5，点G1、G2是椭圆短轴上关于中心O对称的两点，

令｜OA｜＝a，｜OB1｜＝b，｜OG1｜＝d（d＜b），点P是椭圆上任 意 一 点， 记∠G1PG2＝q，则

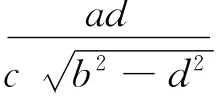
（Ⅱ）若a2＋d2＜2b2，则

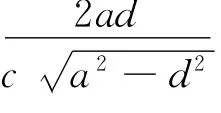
当且仅当点P位于长轴端点时取到.

继续研究，我们得到：

定理6 如图6，点G1、G2是椭圆长轴延长线上关于中心O对称的两点，令｜OA｜＝a，｜OB｜＝b，｜OG1｜＝d（d＞a），点P是椭圆上任意一点，记 ∠G1PG2＝q，则

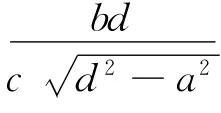
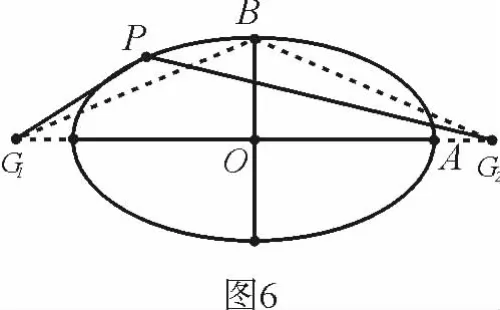
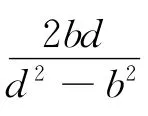
4 可以进一步研究的问题

（1）定理5与定理6的推证过程较繁琐，限于篇幅，此处从略.寻求定理的简洁证明自然成为一个可以进一步研究的问题；

（2）在定理6中，当点G1、G2（非焦点）在长轴上且关于中心O对称时，椭圆上的点对这两点的张角有怎样的最值？

1 贺德光.椭圆中两类张角最大值的推求及其应用［J］.数学通讯，2005（24）